Réflexion autour du Dobble dual
En juin dernier, j’avais réalisé un jeu de Dobble maison. Voici une petite ébauche de réflexion autour de ce qu’on pourrait appeller un Dobble dual.
Un jeu de Dobble est un ensemble de N cartes proposant chacune M symboles. Le jeu est construit de telle façon qu’en choisissant deux cartes au hasard, on est assuré d’avoir exactement un symbole en commun entre les deux cartes. L’objectif du jeu est donc de répérer rapidement l’unique point commun entre deux cartes.
Dans un jeu de Dobble dual, j’aimerais considérer le problème inverse : repérer rapidement le ou les intrus. Comme on s’apprête à le voir, le nombre d’intrus souhaité va conduire à différentes solutions.
- Dobble d’ordre 2
- Dobble d’ordre 3
- Dobble d’ordre quelconque
- Une autre définition du Dobble dual
- Une autre piste de création de Dobble dual
Dobble d’ordre 2
Avec uniquement deux symboles par carte, il est immédiat de constater que Dobble et Dobble dual sont identiques : chercher l’élément commun entre deux cartes revient à repérer l’intrus
Notons qu’on peut également définir un jeu de Dobble dual d’ordre 2 d’une taille arbitrairement grande pour peu qu’on dispose d’un catalogue de symbole conséquent : “AB”, “AC”, “AD”, “AE” etc… L’intérêt ludique est toutefois assez limité.
Dobble d’ordre 3
Avec 3 symboles par carte, la situation est assez similaire. J’appelle nombre d’intrus le nombre $M_i$ de symboles qui différent sur chaque carte. Ainsi dans un jeu de Dobble normal d’ordre M, il y a M-1 intrus.
Si on souhaite un jeu avec deux intrus, alors le problème admet au moins une solution puisqu’à nouveau Dobble et Dobble dual sont confondus.
Si on souhaite un jeu avec un seul intrus (et donc exactement deux symboles identiques sur trois) alors nous retrouvons déjà la solution triviale exposée dans le cas précédent.
Mais nous pouvons aussi partir d’un alphabet de $M+1 = 4$ symboles et en éliminer un à chaque fois. Nous avons ainsi :
| Alphabet | Symbole supprimé | Carte | Symboles |
|---|---|---|---|
| ABCD | D | 1 | ABC |
| ABCD | C | 2 | ABD |
| ABCD | B | 3 | ACD |
| ABCD | A | 4 | BCD |
Donc un jeu de Dobble dual avec 3 symboles par carte :
- pour deux intrus, le jeu maximal possède 7 cartes : c’est le jeu de Dobble d’ordre 3
- pour un intrus, il existe un jeu dual trivial d’une taille arbitrairement grande
- pour un intrus, il existe un jeu de 4 cartes construit sur un alphabet de 4 symboles
Dobble d’ordre quelconque
Notre algorithme se généralise facilement. Par exemple, si je souhaite un intrus par carte et 8 symboles par carte, j’obtiens le tableau suivant :
| Alphabet | Symbole supprimé | Carte | Symboles |
|---|---|---|---|
| ABCDEFGHI | I | 1 | ABCDEFGH |
| ABCDEFGHI | H | 2 | ABCDEFGI |
| ABCDEFGHI | G | 3 | ABCDEFHI |
| ABCDEFGHI | F | 4 | ABCDEGHI |
| ABCDEFGHI | E | 5 | ABCDFGHI |
| ABCDEFGHI | D | 6 | ABCEFGHI |
| ABCDEFGHI | C | 7 | ABDEFGHI |
| ABCDEFGHI | B | 8 | ACDEFGHI |
| ABCDEFGHI | A | 9 | BCDEFGHI |
Ainsi entre la carte 7 et la carte 9, l’intrus sera le couple “A-C”.
D’une façon générale, avec $M$ symboles par carte, l’algortihme nécessite un alphabet de $P=M+1$ symboles et nous obtenons à la fin un jeu de $N = M+1$ cartes.
Une autre définition du Dobble dual
Une solution amusante serait de partir de la matrice de connectivité du Dobble normal et de prendre son complémentaire.
Pour rappel, il s’agit d’une matrice carrée de dimension $N= 1 + M(M-1)$, notée $A$, et dont les élément $a_{i,j}$ valent 1 si et seulement si le symbole $i$ apparaît sur la carte $j$. Dans le cas contraire, on a $a_{i,j} = 0$.
Nous définissions la matrice duale $\bar{A}$ de la façon suivante :
- si $a_{i,j} = 0$ alors $\bar{a}_{i,j} = 1$
- si $a_{i,j} = 1$ alors $\bar{a}_{i,j} = 0$
Si je note $c_i$ les élements de la carte $i$ du jeu de Dobble normal, alors on a :
- $c_i \lor c_j$ vaut 1 sur exactement $2M-1$ cartes (et 0 sinon)
- $c_i \land c_j$ vaut 1 sur exactement 1 carte (le symbole commun) et 0 sinon
On a immédiatement :
\[\neg c_i\land \neg c_j = \neg ( c_i \lor c_j )\]On en déduit donc que les cartes du jeu de Dobble dual tel qu’on l’a définit :
- posséderont chacune $\overline{M} = N - M$ symboles par carte
- posséderont toujours exactement $N - 2M + 1$ symboles communs.
Voici quelques valeurs de la taille $P$ de l’alphabet (commune avec le Dobble normal), du nombre de cartes $N$ (commun avec le jeu de Dobble normal) ainsi que le nombre de symboles commun $M_c$ (différent du cas du Dobble normal où $M_c=1$) et du nombre d’intrus $M_i$ (différent du cas du Dobble normal où $M_i=M-1$) pour les premières valeurs du nombre de symbole par carte $M$. On a bien entendu $M_c+M_i = M$.
| Symboles par carte $M$ | Symboles par carte $\bar{M}$ | Taille de l’aphabet $P$ | Nombre de cartes $N$ | Symboles en commun $M_c$ | Symboles intrus $M_i$ |
|---|---|---|---|---|---|
| 3 | 4 | 7 | 7 | 2 | 2 |
| 4 | 9 | 13 | 13 | 6 | 3 |
| 6 | 25 | 31 | 31 | 20 | 5 |
| 8 | 49 | 57 | 57 | 42 | 7 |
| 12 | 121 | 133 | 133 | 110 | 11 |
| 14 | 169 | 183 | 183 | 156 | 13 |
Ainsi, partant d’un jeu de Dobble à $M=6$ symboles par carte, j’obtiens un Dobble dual de 25 symboles par cartes. Pour deux cartes quelconques de ce jeu dual, j’aurai exactement 5 intrus à détecter (et donc 20 symboles communs).
Les matrices de connectivité $A$ et $\bar{A}$ sont données ci-dessous (un pixel noir signifie une valeur à 1).
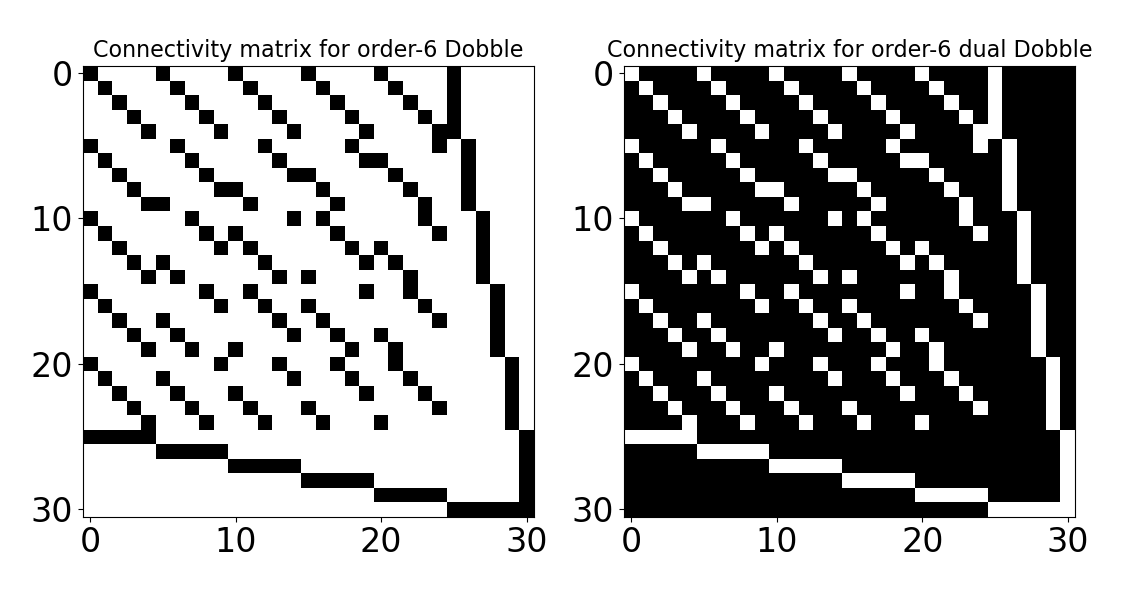
Si nous définissons l’alphabet de symboles comme étant les 26 lettres majuscules suivies des 26 lettres minuscules alors les 31 cartes de notre Dobble dual d’ordre 6 sont :
- Card 01 : ['B', 'C', 'D', 'E', 'G', 'H', 'I', 'J', 'L', 'M', 'N', 'O', 'Q', 'R', 'S', 'T', 'V', 'W', 'X', 'Y', 'a', 'b', 'c', 'd', 'e']
- Card 02 : ['A', 'C', 'D', 'E', 'F', 'H', 'I', 'J', 'K', 'M', 'N', 'O', 'P', 'R', 'S', 'T', 'U', 'W', 'X', 'Y', 'a', 'b', 'c', 'd', 'e']
- Card 03 : ['A', 'B', 'D', 'E', 'F', 'G', 'I', 'J', 'K', 'L', 'N', 'O', 'P', 'Q', 'S', 'T', 'U', 'V', 'X', 'Y', 'a', 'b', 'c', 'd', 'e']
- Card 04 : ['A', 'B', 'C', 'E', 'F', 'G', 'H', 'J', 'K', 'L', 'M', 'O', 'P', 'Q', 'R', 'T', 'U', 'V', 'W', 'Y', 'a', 'b', 'c', 'd', 'e']
- Card 05 : ['A', 'B', 'C', 'D', 'F', 'G', 'H', 'I', 'K', 'L', 'M', 'N', 'P', 'Q', 'R', 'S', 'U', 'V', 'W', 'X', 'a', 'b', 'c', 'd', 'e']
- Card 06 : ['B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'K', 'L', 'M', 'O', 'P', 'Q', 'S', 'T', 'U', 'W', 'X', 'Y', 'Z', 'b', 'c', 'd', 'e']
- Card 07 : ['A', 'C', 'D', 'E', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'P', 'Q', 'R', 'T', 'U', 'V', 'X', 'Y', 'Z', 'b', 'c', 'd', 'e']
- Card 08 : ['A', 'B', 'D', 'E', 'F', 'H', 'I', 'J', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'U', 'V', 'W', 'Y', 'Z', 'b', 'c', 'd', 'e']
- Card 09 : ['A', 'B', 'C', 'E', 'F', 'G', 'I', 'J', 'K', 'M', 'N', 'O', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Z', 'b', 'c', 'd', 'e']
- Card 10 : ['A', 'B', 'C', 'D', 'F', 'G', 'H', 'J', 'K', 'L', 'N', 'O', 'P', 'R', 'S', 'T', 'V', 'W', 'X', 'Y', 'Z', 'b', 'c', 'd', 'e']
- Card 11 : ['B', 'C', 'D', 'E', 'F', 'G', 'H', 'J', 'K', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'U', 'V', 'X', 'Y', 'Z', 'a', 'c', 'd', 'e']
- Card 12 : ['A', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'K', 'L', 'N', 'O', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'Y', 'Z', 'a', 'c', 'd', 'e']
- Card 13 : ['A', 'B', 'D', 'E', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'O', 'P', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Z', 'a', 'c', 'd', 'e']
- Card 14 : ['A', 'B', 'C', 'E', 'F', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'P', 'Q', 'S', 'T', 'V', 'W', 'X', 'Y', 'Z', 'a', 'c', 'd', 'e']
- Card 15 : ['A', 'B', 'C', 'D', 'F', 'G', 'I', 'J', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'T', 'U', 'W', 'X', 'Y', 'Z', 'a', 'c', 'd', 'e']
- Card 16 : ['B', 'C', 'D', 'E', 'F', 'G', 'I', 'J', 'K', 'L', 'M', 'N', 'P', 'R', 'S', 'T', 'U', 'V', 'W', 'Y', 'Z', 'a', 'b', 'd', 'e']
- Card 17 : ['A', 'C', 'D', 'E', 'F', 'G', 'H', 'J', 'L', 'M', 'N', 'O', 'P', 'Q', 'S', 'T', 'U', 'V', 'W', 'X', 'Z', 'a', 'b', 'd', 'e']
- Card 18 : ['A', 'B', 'D', 'E', 'F', 'G', 'H', 'I', 'K', 'M', 'N', 'O', 'P', 'Q', 'R', 'T', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'd', 'e']
- Card 19 : ['A', 'B', 'C', 'E', 'G', 'H', 'I', 'J', 'K', 'L', 'N', 'O', 'P', 'Q', 'R', 'S', 'U', 'W', 'X', 'Y', 'Z', 'a', 'b', 'd', 'e']
- Card 20 : ['A', 'B', 'C', 'D', 'F', 'H', 'I', 'J', 'K', 'L', 'M', 'O', 'Q', 'R', 'S', 'T', 'U', 'V', 'X', 'Y', 'Z', 'a', 'b', 'd', 'e']
- Card 21 : ['B', 'C', 'D', 'E', 'F', 'H', 'I', 'J', 'K', 'L', 'N', 'O', 'P', 'Q', 'R', 'T', 'U', 'V', 'W', 'X', 'Z', 'a', 'b', 'c', 'e']
- Card 22 : ['A', 'C', 'D', 'E', 'F', 'G', 'I', 'J', 'K', 'L', 'M', 'O', 'P', 'Q', 'R', 'S', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'e']
- Card 23 : ['A', 'B', 'D', 'E', 'F', 'G', 'H', 'J', 'K', 'L', 'M', 'N', 'Q', 'R', 'S', 'T', 'U', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'e']
- Card 24 : ['A', 'B', 'C', 'E', 'F', 'G', 'H', 'I', 'L', 'M', 'N', 'O', 'P', 'R', 'S', 'T', 'U', 'V', 'X', 'Y', 'Z', 'a', 'b', 'c', 'e']
- Card 25 : ['A', 'B', 'C', 'D', 'G', 'H', 'I', 'J', 'K', 'M', 'N', 'O', 'P', 'Q', 'S', 'T', 'U', 'V', 'W', 'Y', 'Z', 'a', 'b', 'c', 'e']
- Card 26 : ['F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd']
- Card 27 : ['A', 'B', 'C', 'D', 'E', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd']
- Card 28 : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd']
- Card 29 : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'U', 'V', 'W', 'X', 'Y', 'Z', 'a', 'b', 'c', 'd']
- Card 30 : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'Z', 'a', 'b', 'c', 'd']
- Card 31 : ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T', 'U', 'V', 'W', 'X', 'Y']
Les intrus entre la carte 1 et la carte 2 sont les cinq couples “A-B”, “F-G”, “K-L”, “P-Q” et “U-V”.
Ces cartes ont été obtenues à l’aide du bout de script ci-dessous.
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Thu Sep 16 22:25:07 2021
@author: DonutMan
@license: GPL
"""
import sys
from sympy import isprime
import numpy as np
from matplotlib import pyplot as plt, rc
M = 4 # Ordre du Dobble
M = 6
p = M-1 # Ordre du plan projectif sous-jacent
N = 1+M*(M-1) # Total number of symbols
# Symboles
s_lower = [chr(i) for i in range(97,97+26)]
s_upper = [chr(i) for i in range(65,65+26)]
s = s_upper.copy()
s.extend(s_lower)
# Sanity check
if not isprime(p):
sys.exit('Error : M-1 = %d is not prime !' % p)
# Sanity check
if N > len(s):
sys.exit('Error : cannot map the requested Dobble to the alphabet list')
# Construction of the connectivity matrix
# A(i,j) = True iif the ith symbol belongs to the jth card...
A = np.zeros((N,N), dtype=bool)
x = np.repeat(np.arange(0,p),p)
y = np.tile(np.arange(0,p),p)
# Y=aX+b
a = np.repeat(np.arange(0,p), p)
b = np.tile(np.arange(0,p), p)
for k in range(0, p*p):
A[k, 0:p*p] = (y == np.mod(a[k]*x+b[k], p))
# Special treatment of X=k lines
for k in range(0, p):
A[p*p+k, 0:p*p] = (x == k)
# Line at infinity
A[-1, -p-1::] = True
for k in range(0,p+1):
A[k*p:(k+1)*p, p*p+k] = True
# Dual Dobble
B = np.zeros((N,N), dtype=bool)
B = np.where(A, False, True)
rc('xtick', labelsize=24)
rc('ytick', labelsize=24)
plt.close('all')
plt.figure()
plt.subplot(1,2,1)
plt.imshow(A, cmap='binary')
plt.title('Connectivity matrix for order-%d Dobble' % M, fontsize=16)
plt.subplot(1,2,2)
plt.imshow(B, cmap='binary')
plt.title('Connectivity matrix for order-%d dual Dobble' % M, fontsize=16)
# Now we perform the classification
for iy in range(N):
print('- Card %02d : ' % (iy+1), end='')
print([s[ix] for ix in range(0, N) if A[ix,iy]==0])
Une autre piste de création de Dobble dual
Une autre piste de création de Dobble dual pourrait être l’utilisation de coniques plutôt que de droites dans le calcul de nos intersections.
Une conique est une courbe algébrique plane de degré 2, c’est-à-dire que ses points vérifient l’équation :
\[P(x,y) = a x^2 + 2bxy + c y^2 +2dx +2ey +f = 0\]Le 6-uplet $(a,b,c,d,e,f)$ est le paramètre de la conique et défini sa nature (cercle, ellipse, parabole, hyperbole).
Deux coniques quelconques auront toujours $2\times 2 = 4$ points d’intersection, comptés avec leur multiplicité et définis dans le corps des complexe. Ceci nous amène à deux points importants par rapport aux constructions du Dobble normal :
-
la multiplicité joue ici un rôle plus important qu’auparavant. Les points d’intersection étant les symboles communs entre nos cartes, ceci signifie que, en l’état, certaines cartes pourront avoir jusqu’à 4 symboles identiques en communs !
-
la construction passe désormais obligatoirement dans le corps des complexes. Il n’y a qu’à considérer les deux coniques $x^2+y^2-1 = 0$ et $x^2+y^2-2 = 0$ pour se rendre compte de la nécessité d’avoir des racines complexes, le corps $\mathbb{R}$ n’étant pas algébriquement clos. Ceci amène une difficulté nouvelle dans l’inventaire des symboles.
Mais ceci reste néanmoins une piste potentielle à creuser.