Réalisation d'un jeu de Dobble maison
Cet article est la synthèse d’un petit projet DIY que j’ai eu envie de réaliser : un jeu de Dobble personnalisé !
Ça faisait quelques temps que ça me trottait en tête mais un récent article sur le sujet dans la revue Quadrature a suffit à raviver la flamme.
Plan de l’article
Présentation du jeu
Le Dobble est un jeu de cartes inventé par Play Factory et édité par Asmodée en 2009.
Chaque carte du jeu de Dobble contient 8 symboles. La particularité de ce jeu est que, pour chaque couple de carte, il n’existe qu’un seul symbole en commun entre les deux cartes. Par la suite, on appelle cette particularité la propriété d’unicité.
Dans l’exemple ci-dessous, on remarque ainsi que seul le symbole “Araignée” est commun aux deux cartes.

Il y a plusieurs façon d’y jouer. Par exemple, il faut se débarasser de sa main le plus rapidement possible en empilant les cartes sur un tas commun en citant le symbole commun entre la carte qu’on défausse et la carte située en haut du tas commun.
Le jeu du Dobble est une variante du Problème des quinze écolières, publié en 1850 par le mathématicien britannique Thomas Kirkman dans la revue de mathématiques récréatives “The Lady’s and Gentleman’s Diary”. L’énoncé était le suivant :
« Fifteen young ladies in a school walk out three abreast for seven days in succession: it is required to arrange them daily, so that no two shall walk twice abreast. »
Soit en français :
« Quinze écolières se promènent sept jours de suite par groupes de trois ; il est requis de les grouper par jour de telle sorte que deux écolières ne se promènent jamais deux fois ensemble. »

En 1976, Jacques Cottereau s’inspire de ce problème pour développer le Jeu des insectes (et dont je n’ai hélas pas réussi à trouver trace sur le net). Dans ce jeu, chaque carte contient six images d’insectes et il faut trouver l’insecte commun. L’ancêtre du Dobble est né !
Il faudra ensuite attendre 2008 et la découverte du Jeu des insectes par Denis Blanchot. Cottereau et Blanchot s’associeront ensuite pour développer et commercialiser Dobble.
Dobble, Jeu des insectes et Problème des quinze écolières sont les différentes facettes d’un problème mathématique plus général connu sous le nom de système de Steiner.
Un peu de théorie
Nous considérons par la suite un jeu de $N$ cartes. Chaque carte possède $M$ symboles choisis dans un dictionnaire de $P$ symboles.
On peut tout de suite se poser deux questions :
- pour un triplet $(N,M,P)$ donné, existe-t-il un jeu de Dobble satisfaisant la propriété d’unicité ?
- si un tel jeu existe, comment le construire ?
Ces questions ont déjà été traitées mille fois sur le net, je ne vais pas réinventer l’eau chaude mais juste dégager les deux trois idées clefs.
Parmi la pléthore d’articles dédiés à ce sujet, trois sources remarquables :
- Dobble et la géométrie affine de Maxime Bourrigan sur images.math.cnrs.fr qui propose une belle introduction au sujet,
- Du simple au Dobble de El Jj qui prend un epsilon de hauteur par rapport à tous les autres articles que j’ai pu voir et qui propose des Dobble d’ordre $n$ quelconque. En particulier, il présente la construction d’un Dobble d’ordre (non premier) 4.
- enfin, la revue Quadrature a fait une étude complète du sujet dans son numéro 87 de février-mars 2013.
Premiers résultats
Commençons par l’énoncé de deux propriétés fondamentales du jeu de Dobble qui vont nous permettre de dégager quelques relations.
Propriété 1 Deux cartes de Dobble possèdent toujours exactement un symbole en commun
Propriété 2 Il n’existe pas de symbole qui soit commun à toutes les cartes
Sur une carte de Dobble donnée apparaît $M=8$ symboles. Prenons un symbole au hasard (mettons le Coeur) et comptons le nombre $r$ de cartes qui le contiennent. Il existe nécessairement au moins une autre carte du jeu qui ne contiennent pas le Coeur (car sinon au aurait un jeu de Dobble qui est en contradiction avec la Propriété 2 pour le symbole Coeur). Cette carte ne contient pas le Coeur mais possède néanmoins exactement un symbole en commun avec chacune des $r$ cartes qui possèdent le Coeur. Ce symbole est à chaque fois différent pour chacune des $r$ cartes car sinon cela signifierait que deux cartes auraient à la fois le Coeur et un autre symbole en commun ce qui est contradictoire (toujours en vertu de la Propriété 2).
Étant donné qu’une carte contient exactement $M=8$ symboles, on en déduit que $r$ est au maximum égal à $M$. Ceci nous amène à la formulation de la Propriété 3.
Propriété 3 Un symbole apparaît au maximum $M$ fois
Choisissons maintenant une carte $X$ au hasard. Cette carte contient $M=8$ symboles tous différents. Pour chacun de ces symboles, il existe au plus $M-1$ autres cartes qui possèdent ce symbole commun avec la carte $X$. Il ne saurait y avoir d’autres cartes que ces dernières, car alors elles ne partageraient aucun symbole commun avec la carte $X$. Donc, in fine un jeu de Dobble possède au maximum 1 (la carte X) + $M \times (M-1)$ cartes. Ceci sera notre propriété 4.
Propriété 4 Un jeu de Dobble possède au maximum $1 + M \times (M-1)$ cartes. Donc $N \leq 1 + M \times (M-1)$
Un jeu de Dobble qui contient le nombre maximum de cartes est appelé jeu de Dobble complet. Ainsi le jeu de Dobble possédant $M=8$ symboles par carte, on s’attend à trouver au plus 57 cartes différentes. Or, le jeu en contient en réalité seulement 55 ! Il semblerait que, pour des raisons techniques, les coûts de production étaient beaucoup plus élevés au-delà de $60$ cartes. L’éditeur aurait ainsi préféré sacrifier deux cartes de jeu afin de disposer de cinq “cartes” de règle. Néanmoins, amputer un jeu de Dobble complet ne change absolument pas son fonctionnement. Tout sous-ensemble d’un jeu de Dobble reste un jeu de Dobble.
Par un raisonnement analogue, on peut également quantifier le nombre total $P$ de symboles partant de $M$. Prenons un symbole au hasard (mettons la Voiture pour changer) et extrayons du paquet toutes les cartes qui contiennent ce symbole. En vertu de la Propriété 3, on obtient un ensemble $A$ d’au plus $M$ cartes. Pour chacune de ces cartes, les $M-1$ autres symboles n’apparaissent pas sur les autres cartes de l’ensemble $A$ car cela entrerait en contradiction avec la Propriété 2 (on aurait en commun la Voiture et un autre symbole). Ces symboles étant tous différents, cela nous pose une borne inférieure : il y a au minimum $1 + M \times (M-1)$ symboles différents.
Si maintenant nous faisons l’hypothèse de l’existence d’un symbole $Y$ qui n’apparaît sur aucune des cartes de l’ensemble $A$ alors on obtient également une contradiction. En effet, dans ce cas il existe une carte $X$ portant le symbole $Y$. Prenons une carte de $A$ et cherchons le symbole en commun avec la carte $X$. Par construction, ce ne saurait être ni la Voiture, ni aucun autre symbole présent dans $A$ ce qui est impossible. Nous en arrivons donc à la propriété suivante :
Propriété 5 Un jeu de Dobble possède un alphabet d’exactement $1 + M \times (M-1)$ éléments. Donc $P = 1 + M \times (M-1)$
On le voit, ce qui contraint le dimensionnement du jeu de Dobble c’est le nombre de symboles par carte. Il nous fixe un majorant sur la taille du paquet de cartes et il détermine directement la taille de l’alphabet des symboles.
\[N \leq 1 + M \times (M-1)\] \[P = 1 + M \times (M-1)\]Voici les paramètres envisageables d’un jeu de Dobble avec $M$ symboles par cartes pour les premières valeurs de $M$.
| Avec $M$ symboles par carte | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Je dispose d’au maximun $N$ cartes | 3 | 7 | 13 | 21 | 31 | 43 | 57 | 73 | 91 |
| Mon alphabet contient exactement $P$ symboles | 3 | 7 | 13 | 21 | 31 | 43 | 57 | 73 | 91 |
On appelle ordre d’un jeu de Dobble la valeur de $M$, c’est-à-dire le nombre de symboles par carte. On appelle également jeu complet tout jeu de Dobble comportant le nombre maximal possible de cartes compte tenu de son ordre.
Ensuite, remarquons que ces premiers résultats nous donnent des bornes sur les valeurs admissibles des paramètres $(N,M,P)$ mais ne nous renseignent aucunement sur l’existence de solutions ni même sur leur nombre.
Remarquons également que pour un jeu classique complet, un symbole donné à 8 chances sur 57 d’apparaître sur une carte choisie aléatoirement.
Enfin, les premiers résultats dégagés ici nous empêchent de construire un Dobble par récurrence. Avoir un jeu de Dobble complet d’ordre $M$ ne nous aide a priori pas à construire un jeu de Dobble d’ordre $M+1$.
Dobble d’ordre 2 et théorème de Bezout
Les formules établies précedemment nous indiquent qu’avec deux symboles par carte (donc $M=2$), on a un alphabet d’exactement 3 symboles et au plus 3 cartes différentes. En notant les symboles ${A,B,C}$, on obtient rapidement les trois cartes possibles : “AB”, “BC” et “AC”. Ces trois cartes sont illustrées ci-dessous.
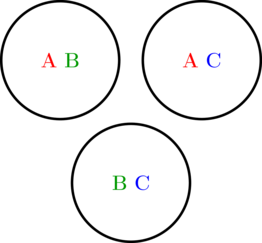
Bien que l’exemple soit assez simple, nous pouvons déjà introduire une analogie qui sera très puissante pour la construction des Dobble d’ordre plus élévé. Comparons les deux énoncés suivants :
Enoncé 1 Deux cartes quelconques possèdent toujours exactement un symbole commun
Enoncé 2 Par deux points distincts passe toujours une et une seule droite
On sent confusément qu’on parle un peu de la même chose. La géométrie planaire pourrait peut-être nous être utile ! En effet, en faisant l’analogie où les symboles sont des droites et les cartes sont des points, on peut représenter le jeu de Dobble d’ordre 2 de la façon suivante :
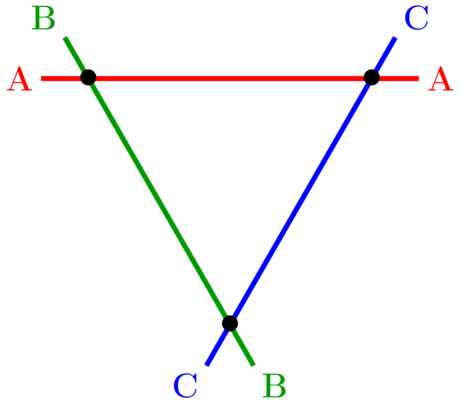
En creusant un peu, on s’aperçoit alors que la construction d’un jeu de Dobble est intimement lié au théorème de Bezout, dont l’énoncé est le suivant :
Théorème de Bezout Deux courbes algébriques projectives complexes planes, sans composante commune, respectivement de degré $n$ et de degré $p$ possèdent exactement $n\times{}p$ points d’intersection, comptés avec leur multiplicité
Dans le cas qui nous intéresse, nous considérons des courbes algébriques planes de degré 1, c’est-à-dire des droites coplanaires. Ces courbes vérifient une équation polynomiale de degré 1 à coefficients $(a,b,c)$ complexes. Cette équation sera de la forme suivante :
\[aX+bY+c = 0\]Le théorème de Bezout nous assure donc de l’existence et de l’unicité d’un point d’intersection entre deux droites distinctes pour peu que les conditions soient favorables. Ces conditions ne sont pas triviales et méritent d’être détaillées.
La coplanarité tout d’abord est nécessaire pour assurer l’existence d’une intersection. Ainsi dans un espace de dimension strictement supérieure à 2, deux droites pourraient très bien ne jamais se couper sans être parallèles pour autant.
L’expression des courbes algébriques dans le corps des complexes nous assure de l’existence des racines. Par exemple, $X^2+1$ n’admet aucune racine réelle mais deux racines complexes $+i$ et $-i$. Le corps des complexes est algébriquement clos mais le corps des réels ne l’est pas. Dans le cas du Dobble ceci dit, cela n’a pas de réelle incidence étant donné qu’un polynôme à coefficients réels de degré 1 aura toujours des racines réelles. Mais néanmoins, la nécessité de travailler sur des corps reste un point critique (nous en verrons une illustration plus loin dans le cas impossible du Dobble d’ordre 7).
Enfin, il est nécessaire de travailler dans le plan projectif pour s’assurer (en l’occurrence) que deux droites distinctes auront toujours une intersection. Ce n’est pas vrai dans le plan usuel puisque deux droites parallèles ne s’intersectent jamais (de façon axiomatique). Dans le plan projectif, deux droites parallèle s’intersecteront en un point situé à l’infini.
Notre analogie quoiqu’il en soit présente une lacune : les symboles et les cartes du jeu de Dobble existent en nombre fini alors qu’il existe une infinité de droites du plan et que chacune de ces droites possède une infinité de points ! Il nous faudra donc par la suite passer en géométrie finie, c’est à dire ne considérer qu’un ensemble fini de points. Nous allons illustrer cette dernière notion dans le cas du jeu de Dobble d’ordre 3.
Dobble d’ordre 3 et plan de Fano
Avec un Dobble d’ordre 3, on s’attend à avoir un alphabet de 7 symboles et un total de 7 cartes différentes.
Commençons par considérer 4 points du plan. Par ces quatre points discrets, nous pouvons faire passer 6 droites qui représentent nos 6 premiers symboles “A”, “B”, “C”, “D”, “E”, et “F”. Il est important de noter qu’aucun autre point n’existe pour le moment : notre géométrie est discrète et non pas continue.
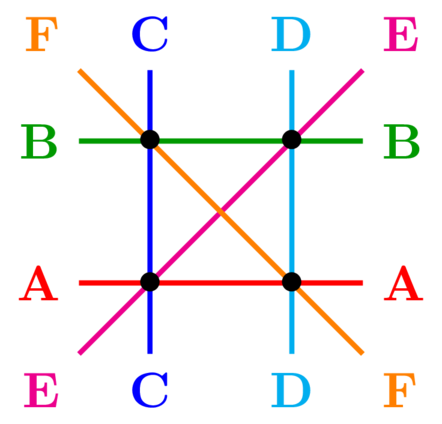
Bien que cela semble être le cas, il est en particulier important de bien réaliser que les droites (E) et (F) ne s’intersectent pas sur cette figure : elles sont parallèles. De même, les droites (A) et (B) sont parallèles ainsi que les droites (C) et (D).
Ce premier schéma nous permet néanmoins de dégager les 4 cartes suivantes : “BCF”, “BDE”, “ACE” et “ADF”. C’est un bon début et on peut vérifier que la propriété d’unicité du Dobble est bien vérifiée. Néanmoins, on sent bien que ce jeu n’est pas complet. On s’attendait à avoir un alphabet de 7 symboles dispersé sur 7 cartes mais on ne manipule que 6 symboles avec seulement 4 cartes… Que nous manque-t-il ?
Ce qu’il nous manque ce sont les points d’intersections des droites parallèles. En l’occurrence, il nous manque les 3 points d’intersections suivants :
- l’intersection entre les droites parallèles (A) et (B)
- l’intersection entre les droites parallèles (C) et (D)
- l’intersection entre les droites parallèles (E) et (F)
Ceci nous introduit 3 nouveaux points qui, selon les axiomes de la géométrie projective, sont situés à l’infini. Par ces trois nouveaux points passeront une et une seule nouvelle droite, appelée droite à l’infini, et que nous notons (G). Cette droite représente notre septième et dernier symbole.
Mettre à jour notre figure nous demande d’abandonner notre perception usuelle des droites : afin de réprésenter les intersections des droites parallèles il est autorisé en géométrie projective de les tordre. Une façon élégante de représenter la figure complète est le plan de Fano dont vous voyez un exemple ci-dessous.
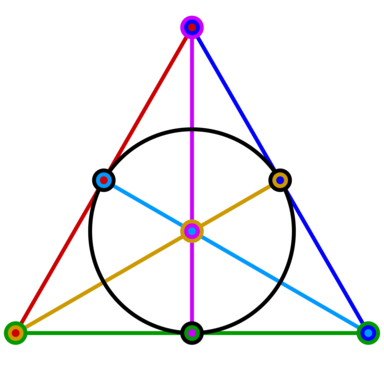
Vous constatez que ce plan contient bien 7 points et définit 7 droites distinctes. En particulier, le cercle noir qui passe par 3 points est bel et bien une droite !
Les trois cartes restantes sont ainsi : “ABG”, “CDG” et “EFG”. Notre jeu de Dobble d’ordre 3 est finalement complet !
Le plan de Fano est un objet très élégant puisqu’il s’agit du plus petit plan projectif fini. C’est le plan projectif $F_2$ basé sur le corps fini à deux éléments $\mathbb{Z}/2\mathbb{Z}$. Nous allons détailler un peu plus la définition de ce corps dans la section suivante car cela nous sera très utile par la suite.
Corps fini $\mathbb{Z}/p\mathbb{Z}$
Commençons par présenter rapidement l’ensemble $\mathbb{Z}$ des entiers relatifs. Comme son nom l’indique, cet ensemble contient tous les entiers signés c’est-dire par exemple 0, 1, 2, 3 etc… mais aussi -1, -2 et ainsi de suite. Cet ensemble est infini dénombrable. On peut le munir de toutes sortes de lois. Munissons-le de la loi additive, nous obtenons le groupe $(\mathbb{Z}, +)$. Rajoutons-lui la multiplication et on obtient l’anneau $(\mathbb{Z}, +, \times)$. Nous ne pouvons pas parler de corps des entiers relatifs car cela supposerait l’existence d’inverse pour tout élément de $\mathbb{Z}$ ce qui est faux. Par exemple, il n’existe pas d’entier relatif $n$ qui vérifie $5 \times n = 1$ donc l’entier 5 n’est pas inversible pour la loi multiplicative.
Partant du groupe $(\mathbb{Z}, +)$, il est possible de dériver le groupe quotient $(\mathbb{Z}/n\mathbb{Z}, +)$ qui est un groupe cyclique de cardinal n. Ses éléments sont $\{0,1,2,3,\dots, n-1\}$. De la même manière, on peut parler de l’anneau quotient $(\mathbb{Z}/n\mathbb{Z}, +, \times)$ qui contient les mêmes éléments que le groupe quotient mais qui définit également une multiplication.
On peut montrer qu’un élément $a$ de l’anneau $\mathbb{Z}/n\mathbb{Z}$ est inversible si et seulement si $a$ est premier avec $n$. C’est une conséquence du théorème de Bachet-Bézout. Ainsi on ne peut parler de corps fini $\mathbb{Z}/p\mathbb{Z}$ que si $p$ est premier.
C’est un peu abstrait pour le moment mais nous verrons plus loin que ce théorème a une conséquence directe sur la construction de nos jeux de Dobble.
Dobble d’ordre 4
De la même façon que le jeu de Dobble d’ordre 3 se basait sur le plan de Fano qui est d’ordre 2, nous allons construire le jeu de Dobble d’ordre 4 en nous basant sur le plan projectif $F_3$ engendré par le corps fini $\mathbb{Z}/3\mathbb{Z}$. On remarque ici que 3 étant premier, il nous est permis de parler de corps.
Les éléments de $\mathbb{Z}/3\mathbb{Z}$ sont $\{0,1,2\}$ ce qui nous permet de définir une géométrie initiale de $3 \times 3 = 9$ points.
Sur ces neuf points, nous pouvons définir 4 familles de fonctions affines (donc nos fameuses courbes algébriques de degré 1) :
- les fonctions de la forme $Y = X + k$ avec $0 \leq k < 3$
- les fonctions de la forme $Y = 2X + k$ avec $0 \leq k < 3$
- les fonctions de la forme $X = k$ avec $0 \leq k < 3$
- les fonctions de la forme $Y = k$ avec $0 \leq k < 3$
La figure ci-dessous représente les 9 points du plan ainsi que la droite d’équation $Y=2X$. Les 3 points noirs sont bien alignés !

A chaque point du plan on associe ensuite l’ensemble des droites qui passent par ce point. Si nous attribuons un symbole à chacune de nos droite, il devient alors possible de définir une carte en chaque point de notre géométrie initiale. Comme pour le plan de Fano, il nous faut également ajouter la droite à l’infini qui contiendra l’intersection de nos droites parallèles.
| Fonction | Symbole |
|---|---|
| Y=X+0 | A |
| Y=X+1 | B |
| Y=X+2 | C |
| Y=2X+0 | D |
| Y=2X+1 | E |
| Y=2X+2 | F |
| X=0 | G |
| X=1 | H |
| X=2 | I |
| Y=0 | J |
| Y=1 | K |
| Y=2 | L |
| Droite à l’infini | M |
Ceci nous permet ensuite de définir les combinaisons suivantes pour les 9 points du plan usuel :
| X | Y | Intersection |
|---|---|---|
| 0 | 0 | ADGJ |
| 1 | 0 | CEHJ |
| 2 | 0 | BEIJ |
| 0 | 1 | BEGK |
| 1 | 1 | AFHK |
| 2 | 1 | CDIK |
| 0 | 2 | CFGL |
| 1 | 2 | BDHL |
| 2 | 2 | AEIL |
Ainsi que pour les 4 points appartenant à la droite à l’infini :
| Point à l’infini | Intersection |
|---|---|
| P0 | DEFM |
| P1 | ABCM |
| P2 | DEFM |
| P3 | GHIM |
L’ensemble des $9+4 = 13$ cartes du jeu de Dobble d’ordre 4 sont bien là et ça fonctionne !
Partant de là, il semble aisé de généraliser ce procédé pour un ordre $M$ quelconque. Il suffit de considérer $\mathbb{Z}/(M-1)\mathbb{Z}$ et de lister l’ensemble des droites du plan projectif qui en découle. Mais en réalité cette méthode ne fonctionne que lorsque $(M-1)$ est un nombre premier. Ainsi :
- si $(M-1)$ est premier, alors cette méthode nous permet de construire un Dobble, donc nous assure de l’existence d’au moins une solution
- si $(M-1)$ n’est pas premier, alors cette méthode ne fonctionne pas et ne nous apporte pas d’information sur l’existence (ou non) de solutions
Afin d’illustrer ceci, nous allons tenter de construire un Dobble d’ordre 7, c’est-à-dire basé sur un (hypothétique !) plan projectif d’ordre 6.
Dobble d’ordre 7
Commençons par considérer $\mathbb{Z}/6\mathbb{Z}$, dont les éléments sont $\{0,1,2,3,4,5\}$. On sait que, 6 n’étant pas premier (puisque par exemple $6=2\times 3$) alors $\mathbb{Z}/6\mathbb{Z}$ n’est pas un corps mais un anneau. En particulier, cela signifie qu’il existe des éléments de $\mathbb{Z}/6\mathbb{Z}$ qui ne sont pas inversibles.
Voici la table de multiplication dans $\mathbb{Z}/6\mathbb{Z}$. On remarque que mis-à-part 1 et 5 qui sont leur propre inverse, les autres éléments ne sont pas inversibles.
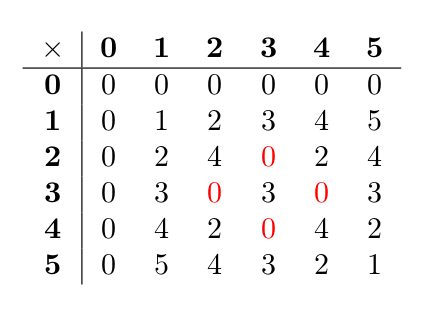
En particulier, si nous traçons les deux droites d’équation $Y=2X$ d’une part et $Y=4X$ d’autre part dans le plan on obtient la figure ci-dessous (en points noirs l’équation $X=2X$, en croix rouge l’équation $X=4X$). On s’aperçoit que ces deux courbes s’intersectent en deux points de coordonnées (0,0) et (3,0). Donc notre méthode produira a minima deux cartes ayant deux symboles communs : ça ne fonctionne plus !

Donc, je me répète, la méthode basée sur les plans projectifs dérivés des corps finis $\mathbb{Z}/p\mathbb{Z}$ ne fonctionne que lorsqu’on travaille sur des corps donc quand $p$ est premier.
Dans le cas général, existe-t-il des solutions ? Cela dépend. Il y a des cas de figures où on sait qu’une construction reste possible (bien qu’un peu plus complexe que ce qui est présenté ici), on sait aussi qu’il y a des cas de figure qui sont impossible (et le Dobble d’ordre 7 en fait partie1) et enfin des cas où la question reste ouverte. Je n’entre pas plus dans les détails mais je vous renvoie au très bon article écrit par El Jj pour plus d’informations.
Dans la suite nous allons nous restreindre au Dobble d’ordre 8. C’est donc le Dobble classique avec 8 symboles par cartes. Comme $7 = 8 -1$ est un nombre premier, l’anneau $\mathbb{Z}/7\mathbb{Z}$ est un corps et la méthode que nous avons détaillée jusqu’ici s’applique.
Un peu de pratique
Dobble d’ordre 8
Voici les combinaisons attendues pour le Dobble d’ordre 8. La construction de ce tableau ne pose pas plus de difficulté que dans le cas du Dobble d’ordre 4 que nous avons présenté dans la partie théorique. Nous manipulons 7 familles de fonctions affines de la forme $Y=aX+b$ avec $1 \leq a < 7$ et $0 \leq b < 7$. Il faut également prendre en compte la famille de fonctions affines de la forme $X=b$ avec $0 \leq b < 7$ ainsi que notre droite à l’infini.
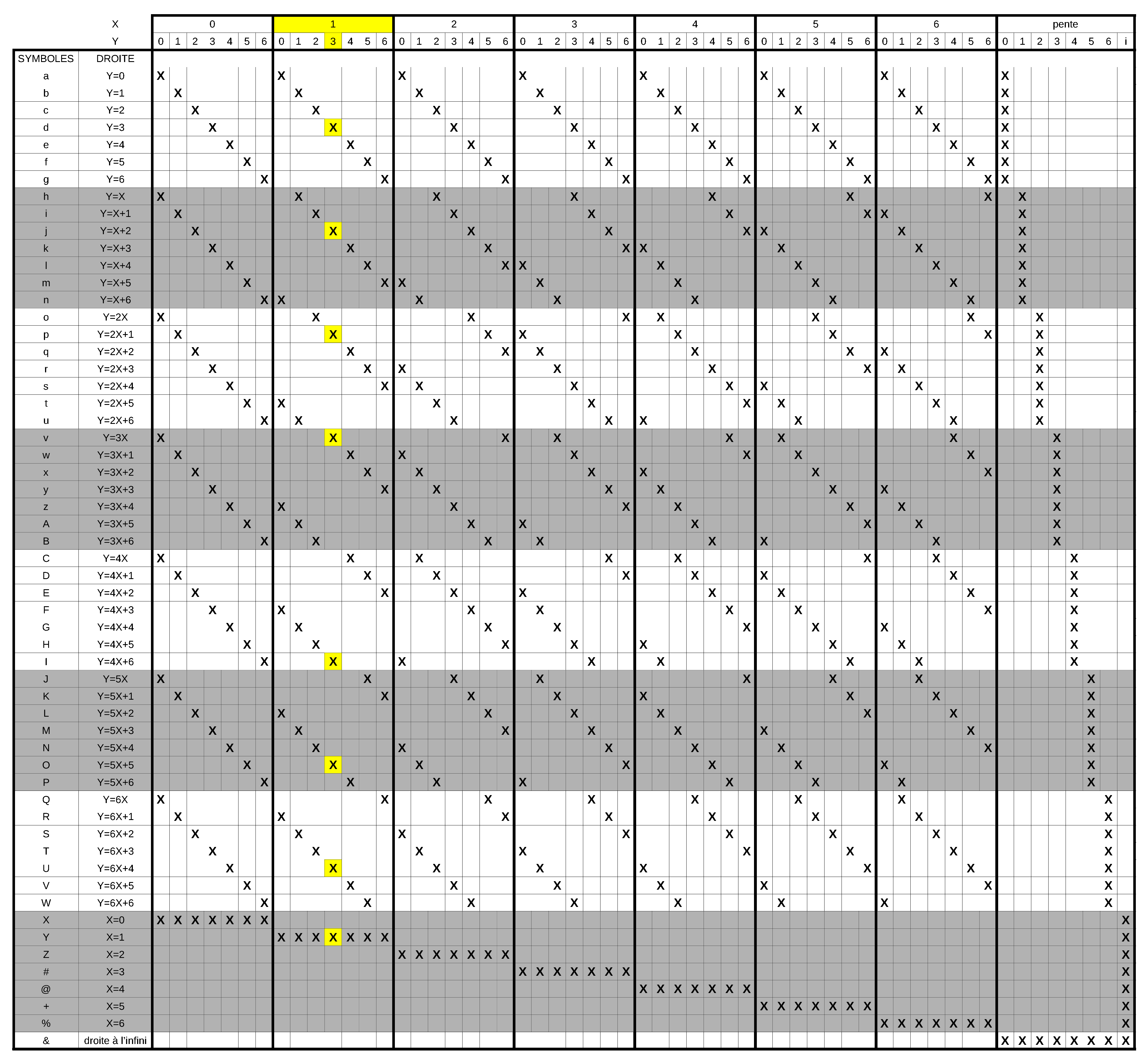
Illustrons le fonctionnement de ce tableau par un exemple (ici surligné en jaune) : notre onzième carte qui est le point de coordonnées $(\textcolor{red}{1},\textcolor{green}{3})$. En ce point s’intersectent exactement 8 droites dont les équations sont respectivement :
- la droite d’équation $Y=3$ puisque $\textcolor{green}{3}=3$,
- la droite d’équation $Y=1X+2$ puisque $\textcolor{green}{3}=1\times{}\textcolor{red}{1}+2$,
- la droite d’équation $Y=2X+1$ puisque $\textcolor{green}{3}=2\times{}\textcolor{red}{1}+1$,
- la droite d’équation $Y=3X+0$ puisque $\textcolor{green}{3}=3\times{}\textcolor{red}{1}+0$,
- la droite d’équation $Y=4X+6$ puisque $\textcolor{green}{3}=4\times{}\textcolor{red}{1}+6$,
- la droite d’équation $Y=5X+5$ puisque $\textcolor{green}{3}=5\times{}\textcolor{red}{1}+5$,
- la droite d’équation $Y=6X+4$ puisque $\textcolor{green}{3}=6\times{}\textcolor{red}{1}+4$,
- la droite d’équation $X=1$ puisque $\textcolor{red}{1}=1$.
Si à chacune des 57 droites est attribué un symbole donné (ici les lettres de l’alphabet en majuscule ou minuscule ainsi que cinq symboles additionnels pour arriver à 57), alors la onzième carte devra porter les symboles “d”, “j”, “p”, “v”, “I”, “O”, “U” et “Y”.
Evaluation de la difficulté
La grande réussite du jeu de Dobble repose sur la méticuleuse attention qui a été portée à la difficulté du jeu. Comme on va le voir par la suite, cette difficulté dépend de plusieurs paramètres :
- de façon immédiate, le nombre $M$ de symboles par carte est un paramètre certain : plus il est élevé, plus le jeu est difficile. Ce paramètre était de 6 pour le jeu des insectes; il est de 8 pour le jeu de Dobble,
- les symboles n’ont pas été choisis au hasard mais peuvent être classés en 7 grandes classes selon leur couleur dominante,
- les symboles ne sont pas régulièrement placés sur le disque mais plutôt éparpillés selon un algorithme que je ne distingue pas (il est aussi possible que cela ait été fait à la main),
- enfin les symboles ont des tailles qui varient d’une carte à l’autre.
J’avais un temps envisagé de générer automatiquement les cartes à l’aide d’un programme, néanmoins je pense que le résultat sera beaucoup plus harmonieux si je construis manuellement chaque carte.
Choix des symboles
Si on observe attentivement les cartes du jeu classique de Dobble (il y a eu plein de variantes mais je ne les connais pas), on s’aperçoit qu’on peut classer l’ensemble des 57 symboles en 7 catégories :
- les 8 symboles Noir & Blanc : zèbre, cadenas, araignée, Yin et Yang, tête de mort, bombe, lunette et cheval d’échec
- les 8 symboles à dominante verte : pomme, dinosaure, cactus, point d’interrogation, tâche de peinture, trèfle, arbre et tortue
- les 9 symboles à dominante orange : bonhomme, clef, biberon, horloge, clef de sol, voiture, marteau, carotte et ancre
- les 8 symboles à dominante bleue : goutte d’eau, dauphin, flocon, fantôme, crayon, igloo, bonhomme de neige et glaçon
- les 8 symboles à dominante jaune : ampoule, fromage, soleil, lune, fleur, chien, point d’exclamation et éclair
- les 8 symboles à dominante rouge : coccinelle, coeur, sens interdit, bouche, cible, flamme, feuille d’érable et clown
- les 8 symboles à dominante violette : toile d’araignée, dobble, oiseau, chat, ciseaux, dragon, bougie et oeil
Ce qui nous fait bien un total de $8\times6 + 9 = 57$ symboles.
Pour être assuré de créer un jeu de Dobble présentant une difficulté similaire au jeu de Dobble classique, il aurait fallu que j’eusse utilisé des symboles avec des dominantes chromatiques. (tiens ça faisait longtemps que je n’avais plus utilisé de subjonctif plus-que-parfait). C’est clairement la contrainte la plus dure à tenir étant donné que j’ai créé le quart des visuels et que je souhaite compléter le deck avec des images issues de la pop-culture. Donc, tant pis j’ai décidé de ne pas tenir compte des couleurs des symboles et de ne choisir que ce qui me plaisait !
Préparation des symboles
J’ai utilisé Gimp pour préparé chacun de mes symboles. Cela a consisté en les étapes suivantes :
- conversion au format png,
- détourage et ajout d’une couche de transparence (afin de mieux gérer la répartition des symboles sur la carte),
- redimensionnement pour avoir une résolution à l’impression d’environ 300 DPI (les symboles font de l’ordre de 2 cm à l’impression donc cela nous donne des symboles de 500 pixels de côté (avec une marge très confortable).
Placement des symboles sur un disque
En observant attentivement la disposition des symboles sur les cartes du Dobble classique, on remarque qu’il y a toujours un symbole vaguement au centre et sept autres symboles qui gravitent autour. Comme je le disais, j’avais envisagé de développer un petit algorithme pour disperser simplement les symboles sur le disque mais ce faisant, il était attendu que les répartitions ne soient guère harmonieuses (en cause : le fait que les symboles soient parfois de taille allongée et la variation d’échelle dont je vais bientôt parler). Pour avoir un résultat convaincant, il aurait fallu développer des choses plus fines et le ratio gain/investissement ne me paraissait pas très intéressant.
Par ailleurs, on remarque que les symboles du jeu de Dobble classique ont des tailles qui varient, ce qui (comme dit plus haut) augmente sensiblement la difficulté du jeu. Voici à titre d’illustration la répartition en taille pour deux symboles quelconque :
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|---|---|---|---|---|---|---|---|---|
| Fromage | 13 mm (100%) | 15 mm (115%) | 15 mm (115%) | 15 mm (115%) | 18 mm (138%) | 18 mm (138%) | 18 mm (138%) | 20 mm (154%) |
| Biberon | 11 mm (100%) | 17 mm (155%) | 18 mm (164%) | 20 mm (182%) | 21 mm (191%) | 23 mm (209%) | 25 mm (227%) | 25 mm (227%) |
Au final, je procède par composition manuelle pour chacune de 57 cartes et je fais varier les tailles au jugé.
J’ai développé un petit script Python qui va ventiler notre bibliothèque de symboles en créant des liens symboliques vers des répertoires qui représenteront nos cartes. Ainsi, pour savoir quels doivent être les symboles de la quinzième carte, il me suffira d’ouvrir le répertoire card_15. Ce dernier contiendra 8 liens symboliques vers les symboles adéquats.
Je sais que je fais beaucoup de disgressions mais je ne résiste pas à rajouter une nouvelle image (ci-dessous). Mon script étant général, je peux lui demander de tracer la matrice de connectivité (l’équivalent du gros tableau ci-dessus) dans le cas d’un Dobble d’ordre 24 (donc avec 24 symboles par carte). Comme 23 est premier, notre méthode fonctionne bien. Notons qu’il faudrait dans ce cas précis un alphabet de 553 symboles !
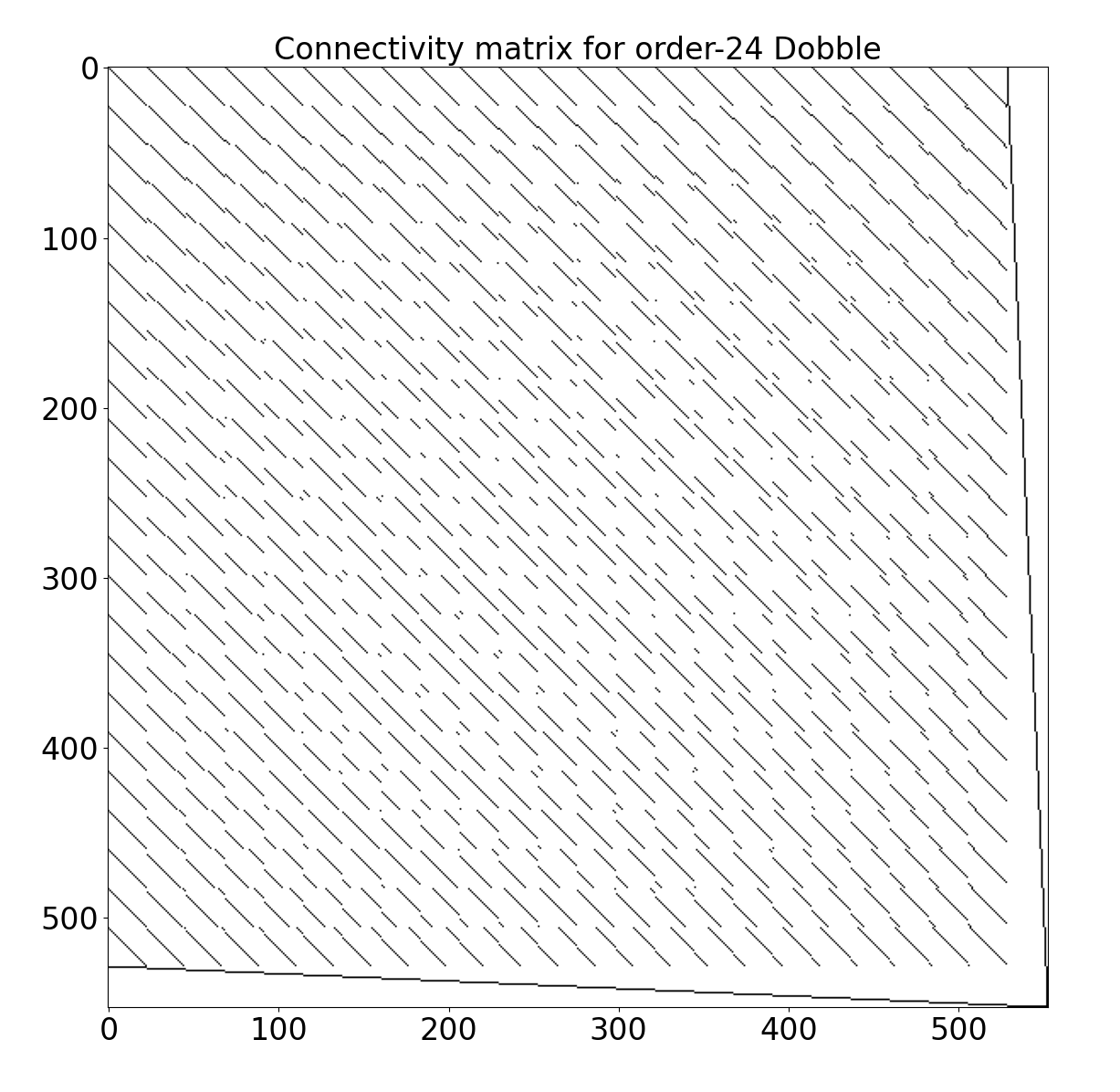
Voici quoiqu’il en soit le script de ventilation.
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Fri Jun 4 19:50:39 2021
@author: DonutMan
@license: GPL
"""
from os import symlink, mkdir
from glob import glob
import sys
from sympy import isprime
import numpy as np
from matplotlib import pyplot as plt, rc
M = 8 # Ordre du Dobble
p = M-1 # Ordre du plan projectif sous-jacent
dir_symbols = '/home/donut/project/dobble/symbols'
dir_cards = './cards/symb'
# Sanity check
if not isprime(p):
sys.exit('Error : M-1 = %d is not prime !' % p)
N = 1+M*(M-1) # Total number of symbols
symbols = glob('%s/*png' % dir_symbols)
if len(symbols) < N:
sys.exit('Error : expected at least %d symbols but got only %d' % (N, len(symbols)))
if len(symbols) > N:
print('Warning : %d symbols will be unused...' % len(symbols)-N)
# Construction of the connectivity matrix
# A(i,j) = True iif the ith symbol belongs to the jth card...
A = np.zeros((N,N), dtype=bool)
x = np.repeat(np.arange(0,p),p)
y = np.tile(np.arange(0,p),p)
# Y=aX+b
a = np.repeat(np.arange(0,p), p)
b = np.tile(np.arange(0,p), p)
for k in range(0, p*p):
A[k, 0:p*p] = (y == np.mod(a[k]*x+b[k], p))
# Special treatment of X=k lines
for k in range(0, p):
A[p*p+k, 0:p*p] = (x == k)
# Line at infinity
A[-1, -p-1::] = True
for k in range(0,p+1):
A[k*p:(k+1)*p, p*p+k] = True
rc('xtick', labelsize=24)
rc('ytick', labelsize=24)
plt.close('all')
plt.imshow(A, cmap='binary')
plt.title('Connectivity matrix for order-24 Dobble', fontsize=24)
# Now we perform the classification
for k in range(0,N):
print('- Creating card %02d/%02d...' % (k+1, N))
symb_list = np.where(A[:,k]==True)[0]
if not len(symb_list) == M: # Something went wrong...
sys.exit('Error : expected %d symbols but got %d...' % (M, len(symb_list)))
mkdir('%s/card_%02d' % (dir_cards, k+1))
for (c, symb) in enumerate(symb_list, 1):
src = symbols[symb]
dst = '%s/card_%02d/symbol_%02d.png' % (dir_cards, k+1, c)
symlink(src, dst)
Voici ce qu’on obtient après exécution de l’algorithme :
$ tree | head -n 19
.
├── card_01
│ ├── symbol_01.png -> /home/donut/symbols/51_alien.png
│ ├── symbol_02.png -> /home/donut/symbols/30_tie_fighter.png
│ ├── symbol_03.png -> /home/donut/symbols/31_lechuck.png
│ ├── symbol_04.png -> /home/donut/symbols/01_donut_man.png
│ ├── symbol_05.png -> /home/donut/symbols/17_cloud.png
│ ├── symbol_06.png -> /home/donut/symbols/07_schtroumpf_lunettes.png
│ ├── symbol_07.png -> /home/donut/symbols/27_dark_vador.png
│ └── symbol_08.png -> /home/donut/symbols/56_sonic.png
├── card_02
│ ├── symbol_01.png -> /home/donut/symbols/57_tentacle.png
│ ├── symbol_02.png -> /home/donut/symbols/20_talisman.png
│ ├── symbol_03.png -> /home/donut/symbols/46_bombe.png
│ ├── symbol_04.png -> /home/donut/symbols/28_dott.png
│ ├── symbol_05.png -> /home/donut/symbols/48_delorean.png
│ ├── symbol_06.png -> /home/donut/symbols/05_seb.png
│ ├── symbol_07.png -> /home/donut/symbols/44_jose_carioca.png
│ └── symbol_08.png -> /home/donut/symbols/56_sonic.png
$ tree | tail -n 20
├── card_56
│ ├── symbol_01.png -> /home/donut/symbols/27_dark_vador.png
│ ├── symbol_02.png -> /home/donut/symbols/44_jose_carioca.png
│ ├── symbol_03.png -> /home/donut/symbols/19_cataseb.png
│ ├── symbol_04.png -> /home/donut/symbols/10_pistolaser.png
│ ├── symbol_05.png -> /home/donut/symbols/40_ice_cream.png
│ ├── symbol_06.png -> /home/donut/symbols/49_cthulhu.png
│ ├── symbol_07.png -> /home/donut/symbols/22_hydralisk.png
│ └── symbol_08.png -> /home/donut/symbols/33_bouyou.png
└── card_57
├── symbol_01.png -> /home/donut/symbols/56_sonic.png
├── symbol_02.png -> /home/donut/symbols/54_rick.png
├── symbol_03.png -> /home/donut/symbols/16_samandmax.png
├── symbol_04.png -> /home/donut/symbols/32_bo.png
├── symbol_05.png -> /home/donut/symbols/15_arbre.png
├── symbol_06.png -> /home/donut/symbols/04_seb_3d.png
├── symbol_07.png -> /home/donut/symbols/03_fire_seb.png
└── symbol_08.png -> /home/donut/symbols/33_bouyou.png
On remarque donc que les cartes 1 et 2 partageront le symbole du fichier 56_sonic.png tandis que les cartes 56 et 57 partageront 33_bouyou.png.
Allez, il ne nous reste plus qu’à réaliser les cartes ! J’ai utilisé cette fois-ci Inkscape et j’ai créé des cartes circulaires de 75 mm de diamètre, identiques au jeu original. Pour le verso, j’ai ajouté un fond perdu de 10 mm de chaque côté, en espérant que ce soit suffisant.
Voici un exemple de carte que j’ai pu obtenir (et qui n’utilise que des dessins de mon cru, mis-à-part pour l’arbre qui vient de openclipart.com) :

Impression et découpe
Une fois les pdf créés, direction l’imprimeur de mon quartier ! Je suis parti sur du papier 300g Digital Silk, dont l’épaisseur et le touché me paraissent très proches du jeu original.
Ensuite, vient la découpe. Plusieurs solutions envisageables :
- aux ciseaux mais je risque d’avoir des découpages polygonaux un peu moches
- au cutter mais j’ai un peu peur d’érafler le papier
- en utlisant un compas à lame mais je laisserai la marque du compas au centre de la carte (centre qu’il faudra par ailleurs identifier…)
- en utilisant une perforatrice circulaire (merci les sites de Scrapbooking…) mais ça ne me paraît pas très précis
Au final, j’ai opté pour les ciseaux qui ont donné un résultat très satisfaisant.
Pour le rangement, j’ai opté pour des boîtes métalliques à visser vues sur le site tinware Direct.
Voici le rendu avant découpe pour mon jeu perosnnalisé à 8 symboles par carte :
Et voici un deuxième jeu, que j’ai réalisé pour ma fille, et qui contient 4 symboles par carte :
Les deux jeux sont parfaitement fonctionnels et, contrairement au jeu de Dobble officiel qui ne contient que 55 cartes pour des raisons de coûts d’impression, ces deux jeux sont complets.
A l’usage, le jeu avec 8 symboles par carte se révèle un peu plus simple que le Dobble officiel. Comme je m’y attendais, ceci est du au fait que les symboles sont très différents les uns des autres rendant le répérage du symbole commun plus simple.
Références
-
Dobble et la géométrie affine de Maxime Bourrigan
-
Du simple au Dobble de El Jj
-
“Jouons un peu… à Dobble !”, Marie et David Hézard dans Quadrature, n°87
-
“Sur des théorèmes de géométrie projective”, Bertand Hauchecorne dans Quadrature n°120
-
“Plans infinis et carrés latins”, Olivier Méjane dans Quadrature n°120
-
Lydie, une orthophoniste plutôt geek a réalisé un Dobble au format texte. C’est notamment en parcourant son tutoriel que je me suis décidé à utiliser Inkscape pour la réalisation des cartes !
-
Marc Deléglise, maître de conférence à l’institut Camille Jordan, a également écrit un billet assez complet sur la question
-
il est bien sûr possible de créer des jeux de Dobble d’ordre 7 mais en aucun cas ces derniers ne pourront être complets. Donc plus précisément : il n’existe aucun jeu de Dobble d’ordre 7 de 43 cartes. ↩

