Etude et simulation de l'effet stenopé
Récemment, en parcourant les réseaux sociaux, je suis tombé sur une énigme de physique amusante. Un homme possède des stores à mailles rectangulaires (grossiérement 2 cm de long et 2 mm de large). Lorsque le Soleil tape directement sur le store, des taches lumineuses se créent dans la pièce.
Si on place une feuille de papier à proximité d’un des trous du store, on voit apparaître une tâche lumineuse de la forme de la maille. Mais si on éloigne suffisamment la feuille, on voit la tâche se déformer pour devenir progressivement circulaire. Pourquoi ?
Il ne s’agit nullement d’un éventuel effet de diffraction. Il suffit, pour s’en convaincre, de remarquer que la dimension du trou (de l’ordre du mm) est très supérieure à la longueur d’onde du faisceau lumineux (de l’ordre de la centaine de nm comme chacun le sait). L’optique géométrique parvient tout à fait à expliquer ce phénomène, qui intervient dans les sténopés et les chambres noires. La tache lumineuse loin de l’écran est circulaire parce que le Soleil (la source) est lui-même circulaire. Ainsi, si le Soleil avait été triangulaire, nous verrions des taches triangulaires.
Je me suis dit que ça pouvait faire un petit billet de blog et ça m’a donné le pretexte d’enfin utiliser la bibliothèque p5.js pour faire des expériences interactives.
Je n’ai plus trop eu le temps de développer ce blog dernièrement et j’ai toujours plusieurs projets dans un coin de ma tête. J’essaie de travailler ici à volume constant : pas plus de quatre soirées en cumulé, rédaction du billet de blog comprise. Le code présenté ici n’est pas parfait et je sais comment l’améliorer…
Plan de l’article
- Plan de l’article
- Cas d’un trou circulaire
- Cas d’un trou rectangulaire
- Calcul intégral
- Calcul géométrique
- Calcul discret
- Améliorations du programme de déformation de tache
Cas d’un trou circulaire
Dans la figure ci-dessous, le Soleil est représenté par un gros trait orange (à gauche). Le sténopé est tracé en trait épais au milieu. En déplaçant la souris sur la figure, nous pouvons modifier la position de l’écran par rapport au petit trou. La portion de l’extérieur accessible est représentée par deux traits verts pointillés. Si le Soleil est en vue, la portion visible apparaît en orange foncé. Tout à droite, vous avez la courbe de luminosité en fonction de la position sur l’écran.
Plus on éloigne l’écran, plus l’ouverture pourra être considérée comme ponctuelle. On se retrouve alors à appliquer une symétrie centrale de centre le milieu de l’ouverture. L’image du Soleil sera donc inversée et parfaitement circulaire. Sa dimension sera proportionnelle au rapport des distances entre source et image. Plus on s’éloigne est plus l’image sera parfaite, en terme de netteté et de stigmatisme. En revanche, la luminosité diminue, ce qui est le compromis classique des stenopés : une image nette nécessitera un écran placé loin du trou (distance trou/écran grande devant la taille du trou) et donc un long temps de pose.
A contrario, en se rapprochant de l’écran, on obtient juste l’image du trou.
Il est amusant de remarquer qu’à une distance donnée, le centre de la tache sera de luminosité constante dont l’intensité sera proportionnelle au carré du rapport entre la portion d’angle capturée par le store et l’angle d’ouverture maximal du Soleil.
Notons que le shéma n’est absolument pas à l’échelle et permet simplement de sentir de quelle façon la tache lumineuse se déforme avec la position de l’écran. En effet, gardons à l’esprit que le Soleil n’est visible de la Terre qu’avec une ouverture angulaire d’environ 0.5°, ce qui est assez petit (environ le quart de l’ouverture d’un pouce placé bras tendu).
Les mathématiques qui sont derrière sont triviales et nécessitent juste d’appliquer le théorème de Thalès. Si nous notons :
- $D$ la distance Soleil-Store
- $d$ la distance Store-Ecran
- $\varepsilon$ le rayon du trou
- $R$ le rayon du Soleil
- $h$ la hauteur du point de l’écran dont on cherche à calculer la luminosité
- $h_1$ et $h_2$ les deux hauteurs limites vues au niveau du plan normal à l’axe optique contenant le Soleil
Alors, nous pouvons avoir une expression de $h_1$ et $h_2$ fonction de tous les autres paramètres du problème :
\[\left\{ \begin{align} h_1 &= -(h+\varepsilon)\cdot{}\frac{D}{d} - \varepsilon \\ h_2 &= -(h-\varepsilon)\cdot{}\frac{D}{d} + \varepsilon \end{align}\right.\]Les valeurs prises par $h_1$ et $h_2$, rapportées au rayon solaire $R$ permettent de remonter à la fraction de flux lumineux transmise par le trou. Cette intensité sera en première approximation1 proportionelle au carré de l’ouverture angulaire maximale rapportée à l’ouverture angulaire de la source.
Chose amusante, si nous connaissons tous les paramètres du problème SAUF la géométrie du trou, alors l’étude du flou de la tâche lumineuse nous permet de reconstruire le profil du trou. On étudie par exemple le profil de luminosité le long d’un axe incliné d’un angle $\theta$ par rapport à l’horizontale. Plus la tache est floue selon cet axe (donc plus le profil de luminosité est étalé) et plus l’ouverture selon cet axe est importante. En faisant varier $\theta$, on explore l’ouverture du trou selon plusieurs axes ce qui nous permettra in fine de reconstruire la géométrie de l’ouverture.
Ci-dessous est tracé le cône de lumière, d’ombre et de pénombre du sténopé. La seconde image ajoute les lignes de niveau de luminosité : on voit apparaître les palliers de luminosité constante que nous avons évoqués.
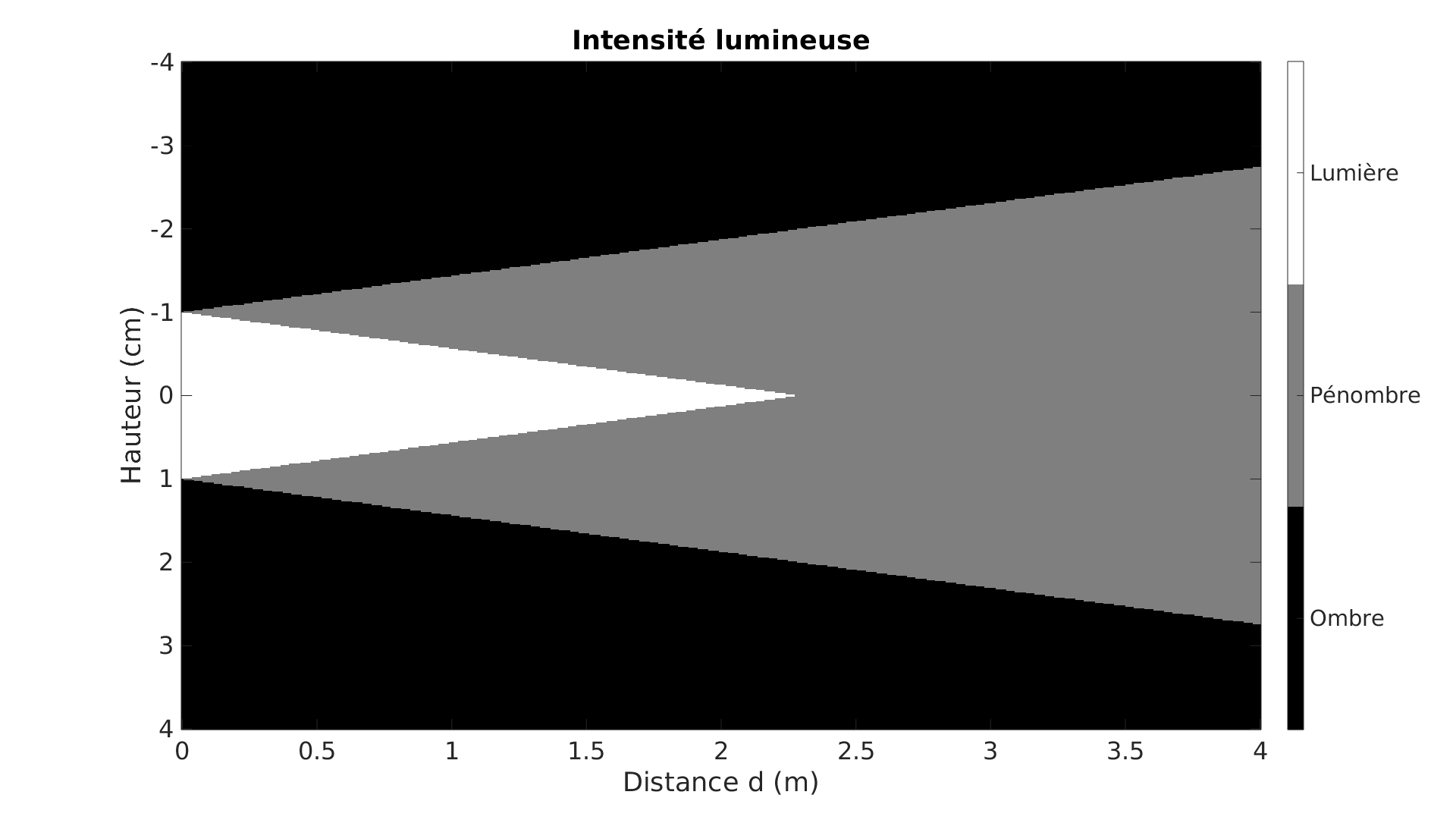
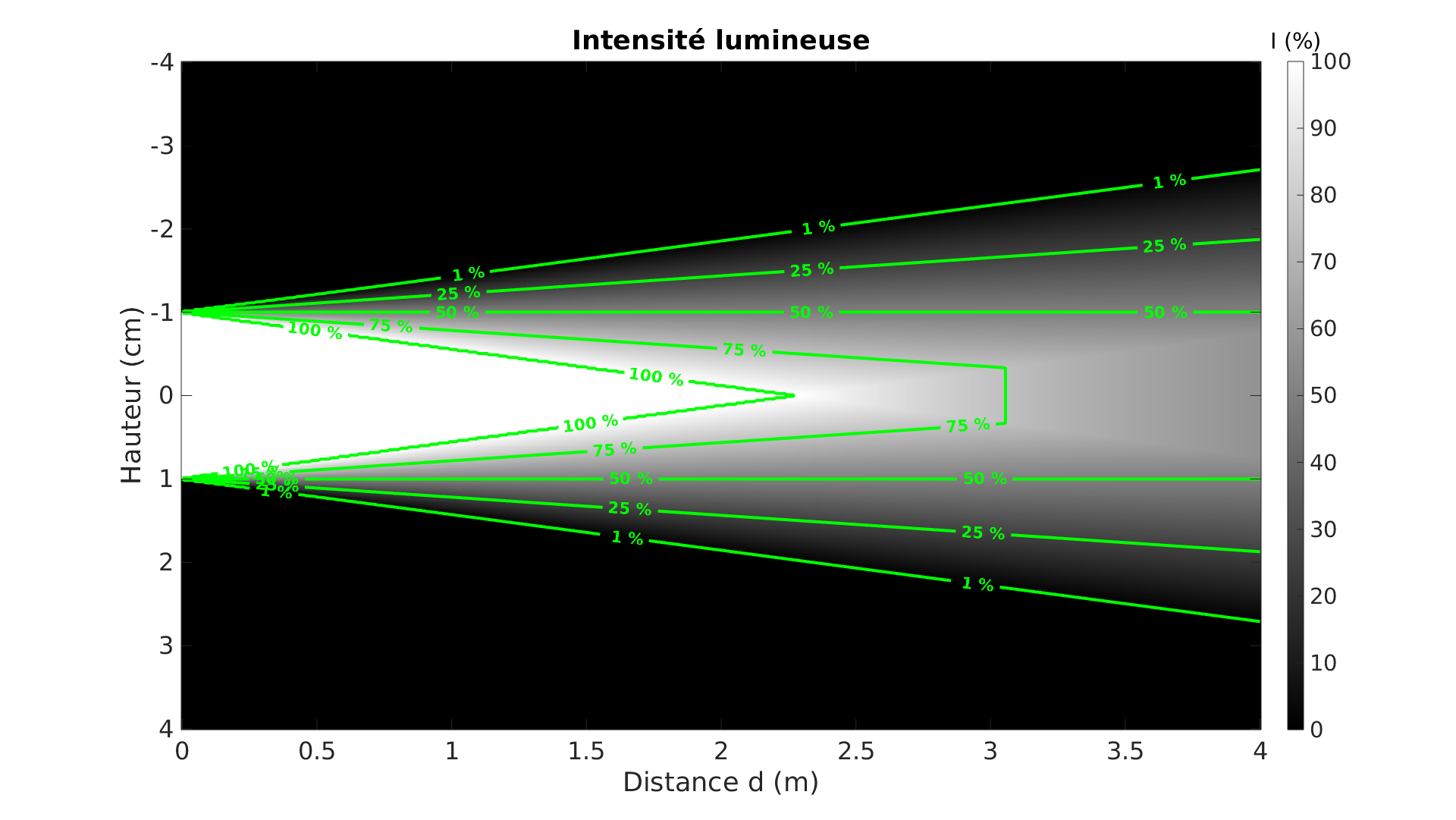
L’hypothèse forte que nous avons faite ici est de considérér un trou circulaire. Comment ce profil de luminosité se modifie-t’il avec des trous de géométrie quelconque ? C’est l’enjeu de la section suivante.
Cas d’un trou rectangulaire
Jusqu’à présent, nous avons considéré une ouverture symétrique et circulaire. Que se passe-t’il si ce n’est pas le cas ?
L’expérience interactive ci-dessous permet de sentir de quelle façon l’ombre se déforme dans le cas d’une ouverture qui ressemblerait à un petit trou de store. Le rectangle rouge c’est le trou du store, le rond vert c’est l’image du Soleil (i.e. l’image qu’on obtiendrait si le trou était ponctuel).
On remarque bien que la tache est plus floue dans la direction horizontale que dans la direction verticale.
Maintenant, parlons un peu du fonctionnement de ce petit programme.
Toute la problématique ici est de calculer la surface de recouvrement entre deux objets du plan du trou :
- un rectangle de côtés $2 e_1$ et $2 e_2$, centré en 0 et représentant l’ouverture du sténopé,
- un disque de centre $(X_c,Y_c)$ et de rayon $R = d \cdot{}tan(\alpha/2)$ représentant l’intersection du cône de lumière avec le plan du trou.
Plusieurs approches sont possibles :
- calcul analytique intégral
- calcul analytique géométrique
- calcul discret
Dans l’expérience interactive ci-dessus, c’est la troisième solution qui a été retenue. Je donne néanmoins ci-dessous quelques éléments de réflexion pour chacune de ces trois solutions.
Calcul intégral
Nous introduisons les fonctions $f_1$ et $f_2$ qui représentent, respectivement l’appartenance au rectangle et au disque :
\[f_1(x,y) = \left\{ \begin{align} 1 &\;\;\textrm{si } |x| < e_1\;\textrm{et}\; |y| < e_2\\ 0 &\;\;\textrm{sinon} \end{align}\right.\] \[f_2(x,y) = \left\{ \begin{align} 1 &\;\;\textrm{si } (x-X_c)^2+(y-Y_c)^2 \leq R\\ 0 &\;\;\textrm{sinon} \end{align}\right.\]Surface du rectangle
Le calcul de la surface du rectangle partant de $f_1$ est assez directe :
\[\mathcal{A} = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f_1(x,y)\,\textrm{d}x\textrm{d}y\]En nous restreignant uniquement sur la zone où $f_1$ est non-nulle, il vient :
\[\mathcal{A} = \int_{-e_1}^{+e_1}\int_{-e_2}^{+e_2} {\color{red}1}\,\textrm{d}x\textrm{d}y\]Ceci nous donne directement la surface attendue, à savoir :
\[\mathcal{A} = 4 e_1 e_2\]Surface du disque
Regardons si nous pouvons également retrouver l’aire du disque :
\[\mathcal{A} = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f_2(x,y)\,\textrm{d}x\textrm{d}y\]En prenant en compte uniquement les zones d’espace où $f_2$ est non-nulle, ceci se réécrit :
\[\mathcal{A} = \int_{x=-R}^{+R}\int_{-R\sin \arccos x/R}^{+R\sin \arccos x/R} {\color{red}1}\,\textrm{d}x\textrm{d}y\]L’intégration sur $y$ est triviale et nous donne :
\[\mathcal{A} = 2 R \int_{-R}^{+R} \sin\left( \arccos \frac{x}{R} \right)\,\textrm{d}x\]Sachant que $\sin \arccos (x) = \sqrt{1-x^2}$, il vient :
\[\mathcal{A} = 2 R \int_{-R}^{+R} \sqrt{1-\left(\frac{x}{R}\right)^2}\,\textrm{d}x\]On introduit le changement de variable $x/R = \sin \theta$, ce qui donne $\textrm{d}x = R \cos \theta \textrm{d}\theta$. On obtient alors l’intégrale suivante, en n’oubliant pas bien sûr d’évaluer les nouvelles bornes d’intégration :
\[\mathcal{A} = 2 R^2 \int_{-\pi/2}^{+\pi/2} \cos^2 \theta\,\textrm{d}\theta = 4 R^2 \int_{0}^{+\pi/2} \cos^2 \theta\,\textrm{d}\theta\]On sait que $2\cos^2(x) = 1 + \cos(2x)$, ce qui donne :
\[\mathcal{A} = 4 R^2 \int_{0}^{+\pi/2} \frac{1}{2} \big[1 + \cos(2\theta)\big]\,\textrm{d}\theta\]Cette intégrale est triviale et nous donne la formule attendue de la surface d’un disque :
\[\mathcal{A} = \pi R^2\]Surface d’intersection d’un disque et d’un rectangle
Après cet échauffement, on attaque le problème central : calculer la surface d’intersection d’un disque et d’un rectangle. Rappelons que ceci nous permettra ensuite de calculer la luminosité en tout point de l’écran.
La surface de recouvrement s’écrit simplement comme étant la double intégrale du produit des deux fonctions $f_1$ et $f_2$ :
\[\mathcal{A} = \int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty} f_1(x,y)\cdot{}f_2(x,y) \,\textrm{d}x\,\textrm{d}y\]On s’en doute, la difficulté proviendra de la prise en compte correcte des bornes d’intégrations en $x$ et en $y$.
Plusieurs cas de figure sont ainsi à considérer selon le nombre de sommets du rectangle inclus dans le disque de lumière. Notons que le disque est une surface convexe : si deux points appartiennent au disque, alors le segment qui relie ces deux points appartiendra également au disque. Ceci a deux conséquences :
- Si l’ensemble des quatres coins du rectangle appartient au disque, alors l’intégralité du rectangle sera contenue dans le disque. L’aire de recouvrement sera alors trivialement l’aire du rectangle.
- En revanche, si aucun des quatres coins du rectangle n’appartient au disque, alors tous les cas de figure sont envisageables, ainsi que l’illustre la figure ci-dessous. Nous pouvons avoir une intersection de surface nulle (cas A), partielle (cas B) ou égale à la surface du disque (cas C).
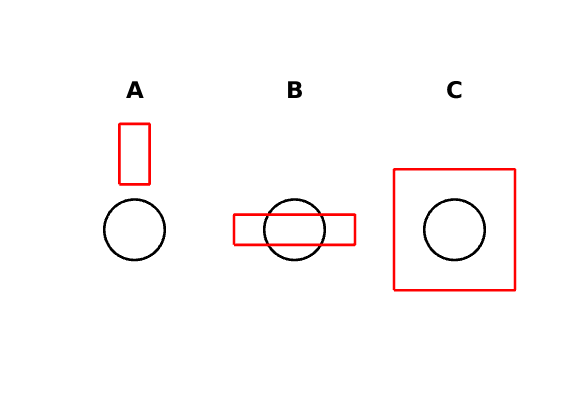
Pour résumer :
- si les 4 sommets sont dans le disque, alors le problème est trivial : l’intensité est proportionnelle au rapport de surface entre rectangle et disque
- si un, deux ou trois sommets appartiennent au disque, alors le calcul est sensiblement identique il faudra juste veiller à convenablement positionner les bornes d’intégration
- si aucun des sommets n’appartient au disque, il faut regarder dans quel cas de figure nous nous trouvons
Je ne vais pas tout détailler mais simplement donner le calcul de la surface de recouvrement dans le cas où exactement un sommet du rectangle appartient au disque.
Soit donc un disque centré en 0 et de rayon $R$ d’une part et soit un point $M$ de coordonnées $(u,v)$ appartenant à ce disque. Nous notons $x_m$ l’abscisse du point appartenant à la fois au bord du rectangle et au disque et ayant même ordonnée que $M$ (voir figure ci-dessous).
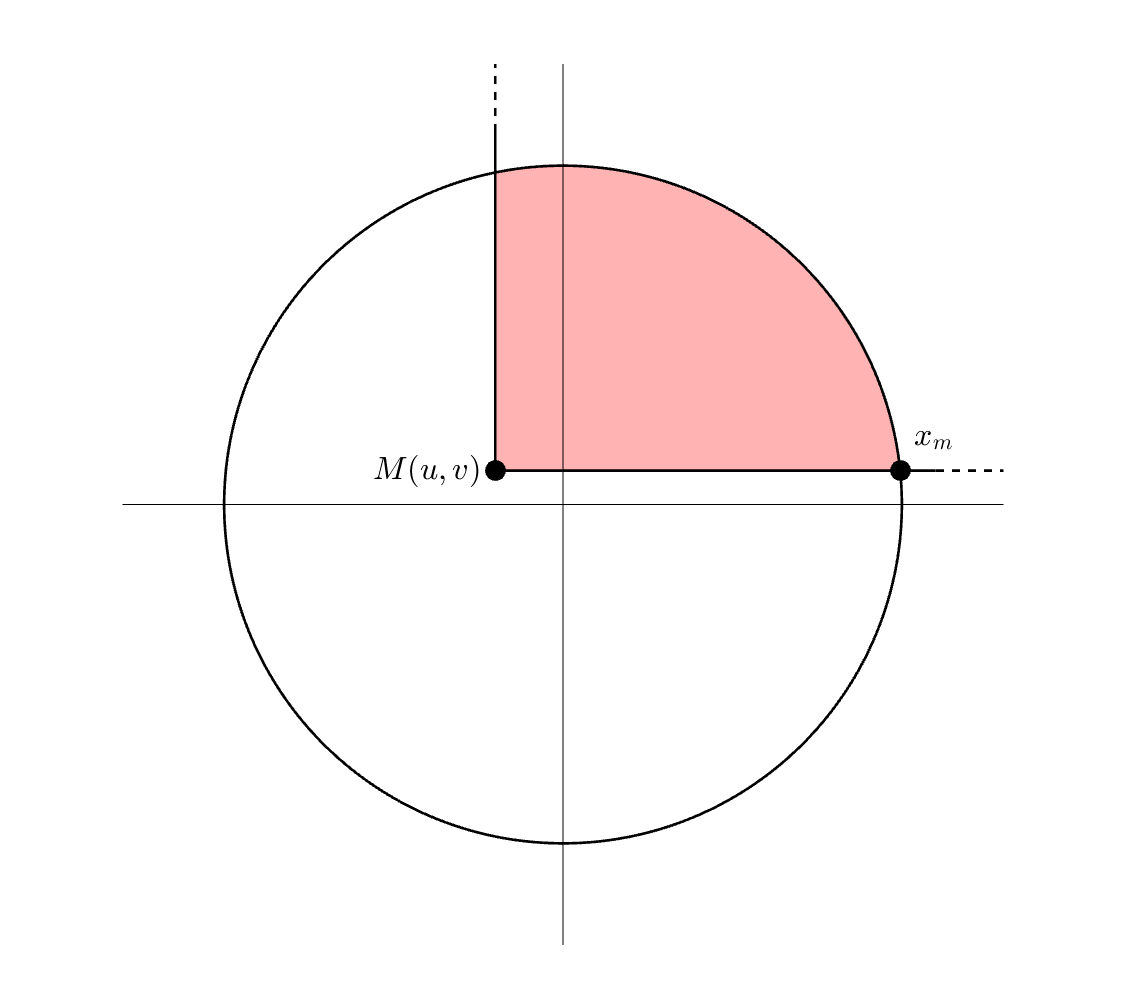
Nous avons :
\[x_m = R \cos \left( \arcsin \frac{v}{R}\right) = R \sqrt{1-\left(\frac{v}{R}\right)^2}\]L’intégrale se réécrit alors :
\[\mathcal{A} = \int_{x = \color{red}u}^{\color{red}x_m}\int_{y=\color{red}v}^{\color{red}R \sin \arccos x/R} 1 \,\textrm{d}x\,\textrm{d}y\]Le reste du calcul est similaire au cas précédent, notons juste qu’au moment de faire le changement de variable $x \to \theta$, les bornes ne sont plus $\pm \pi/2$ mais $\theta_1$ et $\theta_2$ avec :
\[\theta_1 = \arcsin \frac{u}{R} \qquad \theta_2 = \arcsin \frac{x_m}{R}\]On arrive au final à l’expression suivante :
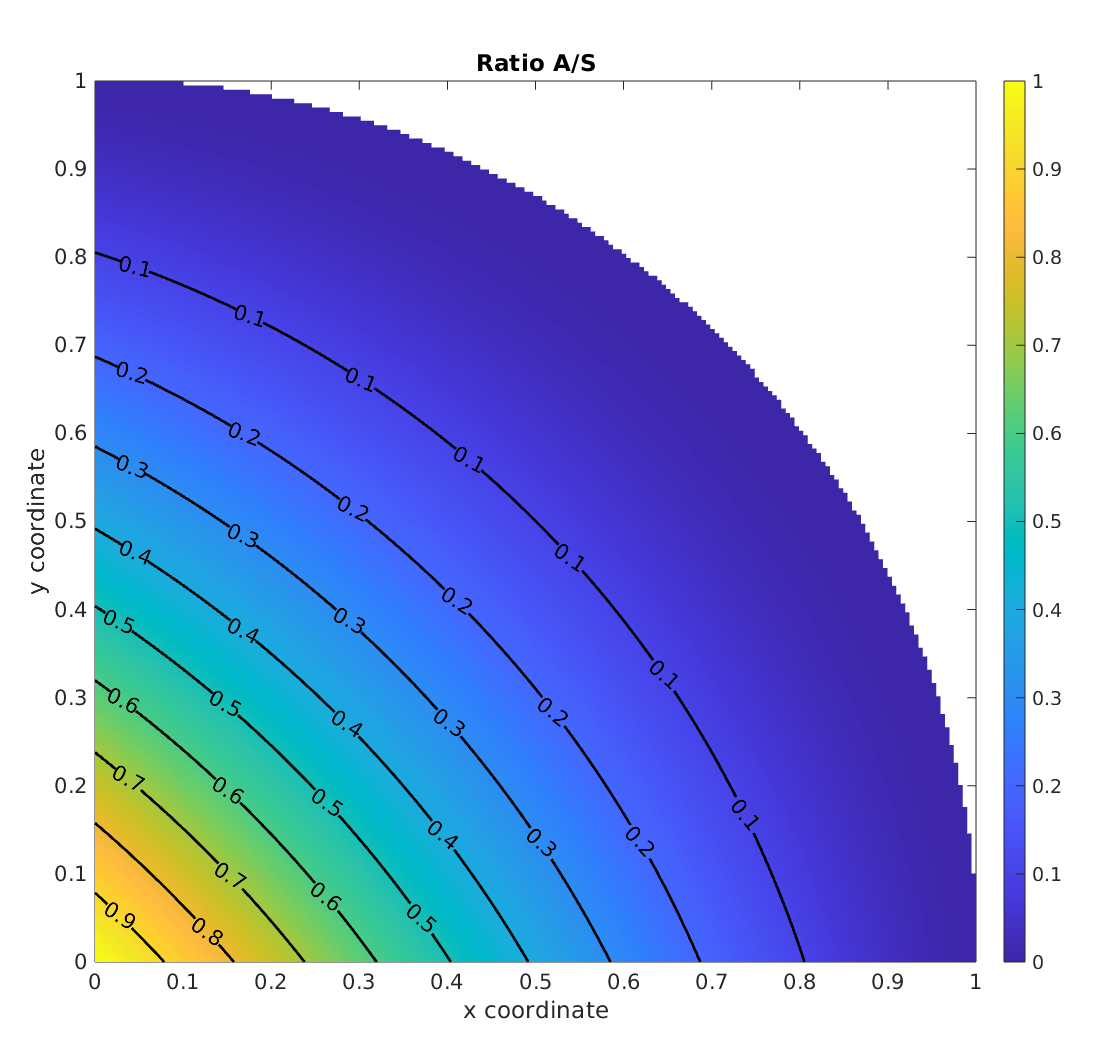
\[\mathcal{A} = \frac{R^2}{2} (\theta_2 - \theta_1) + \frac{R^2}{4} \Big[sin(2\theta_2) - sin(2\theta_1)\Big] - v(x_m-u)\]La figure ci-dessous illustre comment varie la surface $\mathcal{A}$ ramenée à la surface du quart de disque pour différents couples de valeur $(u,v)$ à l’intérieur du quart de disque. Sans surprise, ce ratio est égal à $1$ lorsque $x=y=0$ (autrement dit, le rectangle intersecte intégralement le quart de disque) et tend ensuite vers 0 à mesure qu’on se rapproche du bord du disque.
Calcul géométrique
Nous aurions également pu passer par une approche géométrique pour déterminer la surface d’intersection entre un rectange et un disque.
Nous nous plaçons toujours dans l’hypothèse simplificatrice où un seul sommet du rectangle appartient au disque. Nous supposons par ailleurs que le rectangle n’empiète que sur un seul quadrant du disque.
La figure ci-dessous fait apparaître le quart de disque de rayon $R$ en question ainsi que le point $M(x,y)$ qui est l’unique sommet du rectangle contenu dans le disque. Les points $A$ et $B$ sont les intersections du rectangle avec le cercle. Nous souhaitons au final mesurer la surface $AMB$. Nous découpons alors la surface du quart de disque afin de faire apparaître des relations algébriques entre les surfaces.
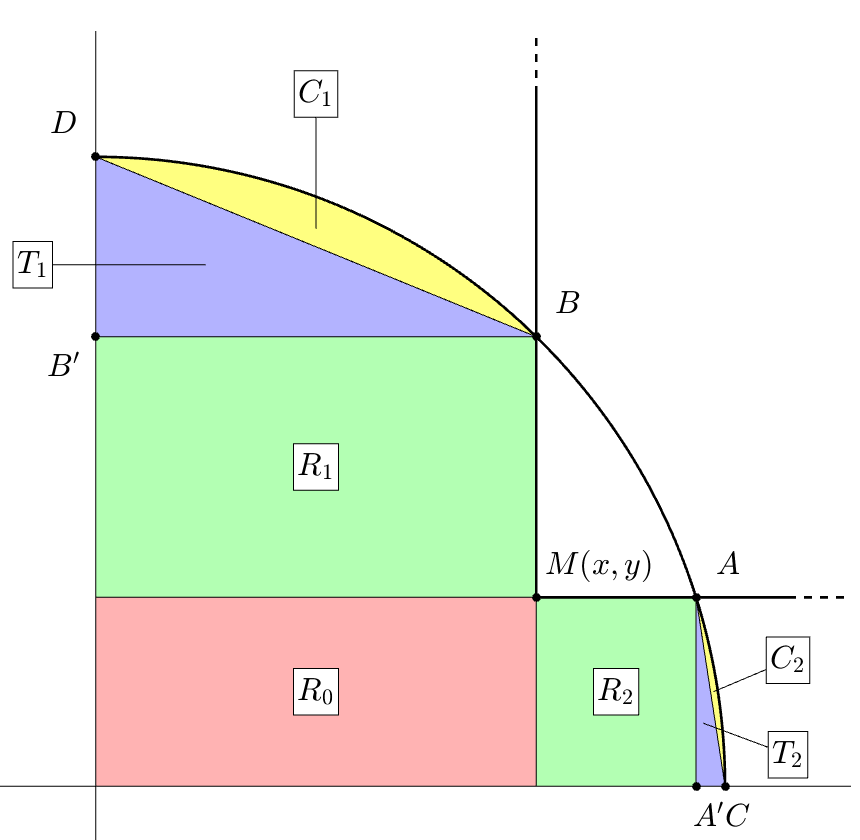
Ce faisant, nous introduisons :
- trois rectangles $R_0$, $R_1$ et $R_2$
- deux triangles $T_1$ et $T_2$
- deux segments circulaires $C_1$ et $C_2$ tendus respectivement par les cordes $BD$ et $AC$
En notant $\mathcal{A}$ l’aire que nous souhaitons mesurer et $S$ l’aire total du quart de disque, nous avons la relation :
\[\mathcal{A} = S - (R_0 + R_1 +R_2 + T_1 + T_2 +C_1 + C_2)\]La principale (petite) difficulté ici est de calculer les coordonnées des points $A$ et $B$. Un peu de trigonométrie nous permet d’établir :
\[A = \left(\begin{matrix}R \sqrt{1 - \left( \frac{y}{R} \right)^2}\\y\end{matrix}\right)\qquad B = \left(\begin{matrix}x\\R \sqrt{1 - \left( \frac{x}{R} \right)^2}\end{matrix}\right)\]Notons que les points $A$ et $B$ forment chacun un angle direct avec l’horizontale, noté respectivement $\theta_A$ et $\theta_B$ :
\[\theta_A = \arctan{y_A/x_A}\qquad \theta_B = \arctan{y_B/x_B}\]Les formules de $R_0$, $R_1$ et $R_2$ sont alors immédiates :
\[\left\{ \begin{align} R_0 &= x\cdot y\\ R_1 &= (y_B - y)\cdot x\\ R_2 &= (x_A - x) \cdot y \end{align} \right.\]Celles de $T_1$ et $T_2$ ne sont guère plus compliquées :
\[\left\{ \begin{align} T_1 &= \frac{1}{2} (1-y_B)\cdot x\\ T_2 &= \frac{1}{2} (1-x_A)\cdot y \end{align} \right.\]Les expressions de $C_1$ et $C_2$ font intervenir l’angle d’ouverture des segments circulaires qui vaut $\alpha_1 = pi/2 - \theta_A$ dans le premier cas et $\alpha_2 = \theta_B$ dans le second cas.
\[\left\{ \begin{align} C_1 &= \frac{r^2}{2}(\alpha_1 - \sin \alpha_1)\\ C_2 &= \frac{r^2}{2}(\alpha_2 - \sin \alpha_2) \end{align} \right.\]Nous avons donc in fine toutes les expressions nous permettant de remonter à la valeur de $\mathcal{A}$ (rappelons juste que l’aire du quart de disque $S$ est égal à $\pi R^2/4$).
Cette formule est strictement équivalente à celle obtenue par calcul intégral. En revanche, son domaine de validité est ici limité au quart de disque.
Calcul discret
Nous venons donc de présenter deux approches pour déterminer analytiquement la valeur d’une intégrale. Nous nous sommes placés dans un premier cas de figure où seul un sommet du rectangle appartient au disque. On pourrait généraliser cela et avoir une formule qui fonctionne en toute généralité. Mais ceci est long et fastidieux.
Une autre solution simple mais approximative consiste à découper l’une des deux formes en éléments de surface élémentaires (par exemple des carrés) et de tester si le centre de chacun de ces éléments appartient à l’autre forme. En sommant les surfaces élémentaires en question, on aboutit à une estimation de la surface de recouvrement. C’est une approche classique d’estimer la valeur numérique de l’intégrale d’une fonction (ici le produit $f_1\cdot{}f_2$).
On peut se demander s’il est plus pertinent de découper le rectangle ou le disque. La réponse, à mon avis, est que cela dépend de la distance de l’écran. Si ce dernier est très proche du store, alors le cercle de lumière est très petit. Pour bien capturer sa surface, il faudrait un maillage du rectangle extrémement fin, ce qui sera coûteux en temps de calcul. On aurait donc plutôt tendance à mailler le disque, et un maillage grossier sera amplement suffisant.
En revanche, lorsqu’on éloigne l’écran, le disque s’agrandit et on se retrouve dans le cas de figure inverse : il sera nécessaire d’avoir un maillage de disque extrémément fin pour bien capturer la surface du rectangle.
La solution la plus élégante serait d’avoir un maillage conditionnel : lorsque l’écran est plutôt proche du mur, on maille le disque; lorsque l’écran est loin du mur, on maille le rectangle. C’est la solution que j’ai retenue ici.
Par ailleurs, on peut également ajouter des tests pour déterminer rapidement si nous sommes dans l’ombre (intensité nulle) ou en pleine lumière (intensité maximale), afin d’éviter le calcul numérique de l’intégrale dans les cas les plus triviaux.
Notons également qu’il existe plusieurs façon de découper nos formes en surfaces élémentaires. Voici par exemple deux découpages du disque envisageables :
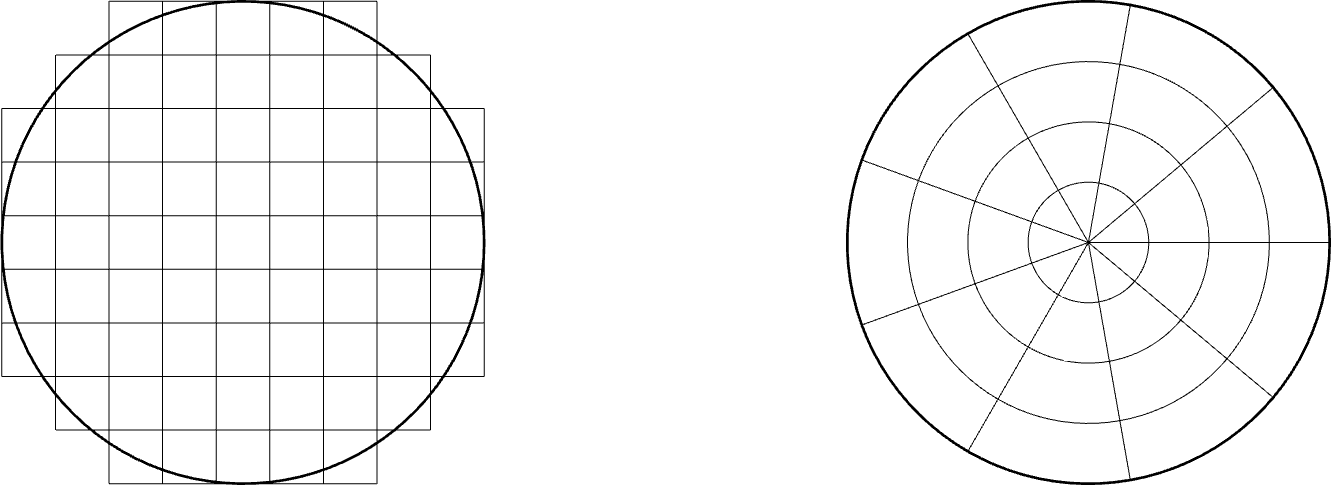
Le découpage sectoriel (à droite) semble plus naturel pour le disque. En particulier, la somme des éléments de surface sera égal à la surface du disque, ce qui n’est pas le cas du découpage en carrés (à gauche). Néanmoins, les surfaces élémentaires n’ont pas toutes la même aire et cela devra être pris en compte dans la sommation.
Plus grave en revanche, avec un découpage sectoriel nous ne serons pas en mesure de convenablement capturer le recouvrement du rectangle, à moins d’avoir un maillage très fin. Ceci est illustré dans la figure ci-dessous.
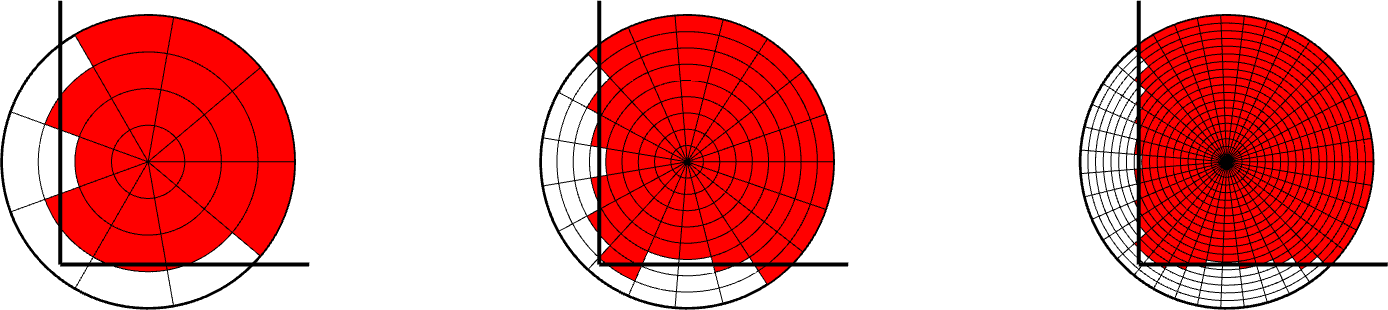
Dans l’expérience interactive présentée en début d’article, j’ai opté pour un maillage carré. J’ai également choisi de travailler à nombre de mailles constant, ce qui était plus simple à programmer et assure un temps de calcul indépendant de la position de l’écran. En revanche, on aura un maillage inutilement fin lorsque le disque est tout petit (i.e. lorsque l’écran est proche du store).
Je n’ai pas non plus pris en compte tous les cas triviaux où le calcul numérique est inutile.
Enfin, ce qui est calculé ici c’est une intensité relative rapportée à l’intensité que nous aurions perçue sans store. En particulier, plus on s’éloigne de l’écran et plus la luminosité baisse (c’est le compromis classique de la chambre noire : on gagne en netteté ce qu’on perd en luminosité). Pour compenser cela, j’ai introduit un facteur qui varie avec le carré de $d$ (le terme au carré s’explique aisément puisque la surface du cercle de lumière évolue lui-même avec $d^2$). Idéalement, il aurait fallu normaliser cela proprement.
Améliorations du programme de déformation de tache
Plusieurs pistes sont envisageables :
- passer à un traitement purement analytique: c’est possible mais fastidieux. Les avantages seront un calcul d’intensité plus juste et plus rapide
- utiliser un maillage dynamique pour travailler à surface élémentaire constante ?
- avoir le choix entre une luminosité relative ou normalisée (et normaliser convenablement le flux lumineux)
-
En toute rigueur, l’intersection de deux disques n’est pas lui-même un disque mais aura une forme de lentille asymétrique, ce qui rend le calcul de la surface réelle plus complexe que ce qui est présenté ici. Néanmoins, cette première modélisation permet, je l’espère, de saisir la dynamique de déformation de la tache lumineuse avec la distance de l’écran. ↩