Etude d'un télescope de Newton

Voici un petit billet rapide pour faire le point sur les différents éléments dimensionnant d’un télescope de Newton. Cette étude ne se veut pas exhaustive (loin de là). Néanmoins je me suis fixé comme objectif de retrouver les principales caractéristiques d’un télescope (grossissement, champ réel, éclairement etc.) en partant de considérations géométriques simples et rigoureuses. Je veux éviter également les formules ad-hoc non justifiées. En fin d’article, je présente également un petit outil que j’ai développé afin de simuler ce qu’on peut espèrer observer dans un télescope.

• Le télescope de Newton
• Etude de chaque élément
  • Le miroir principal
    • Etude du stigmatisme
    • Relation de conjugaison
  • Le miroir secondaire
  • L’oculaire de sortie
• Fonctionnement nominal du télescope
  • Grossissement
  • Champ réel
  • Disque oculaire
  • Photométrie énergétique
• Un petit simulateur de télescope
• Ressources

Le télescope de Newton

Le télescope de Newton est un instrument catadioptrique constitué :

1. d’un miroir primaire généralement parabolique et qui constitue l’objectif
2. d’un miroir secondaire plan dont le but est de déporter l’axe optique sur le côté du tube
3. d’un oculaire qui permet l’observation

Voici comme ces éléments sont disposés au sein de l’intrument (la photo est tirée du site moulin des étoiles).

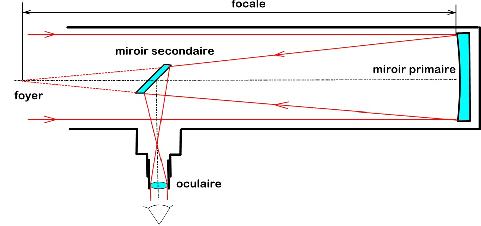
Généralement, le télescope est utilisé en mode afocal c’est à dire que les foyers équivalents sont rejettés à l’infini. Autrement dit, l’oeil observera la cible sans accomodation. Néanmoins, il peut arriver qu’on décide de placer la cible à distance finie (typiquement au punctum proximum). On peut également placer un appareil photo au foyer du miroir primaire ce qui nous permer de bénéficier des capacités d’intégration de l’appareil.

Etude de chaque élément

Le miroir principal

Le miroir principal d’un télescope de Newton est un miroir parabolique.

Une parabole est l’ensemble des points du plan à équidistance entre une droite (la directrice, notée ici $(\Delta)$) et un point (le foyer, noté ici $F$). Pour tout point $M$ de la parabole, en notant $H$ son projeté orthogonal sur $(\Delta)$, nous avons donc :

\[||HM|| = ||FM||\]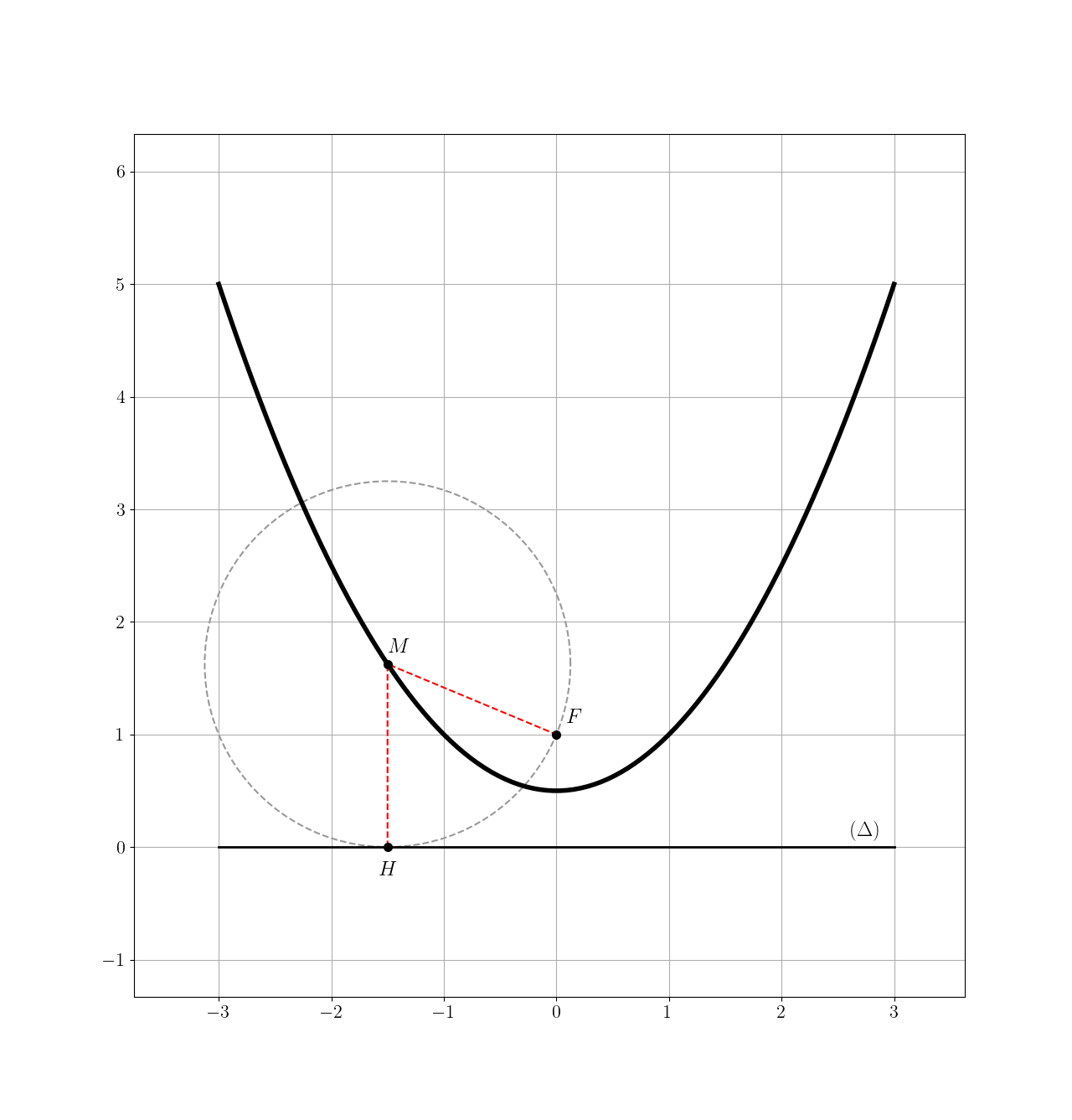

Etude du stigmatisme

En traçant quelques rayons d’une source placée à l’infini sur l’axe optique (que nous noterons $A$ par la suite), on observe que tous les rayons sont renvoyés vers le foyer : il y a stigmatisme. L’image du point $A$ est exactement le point $F$.

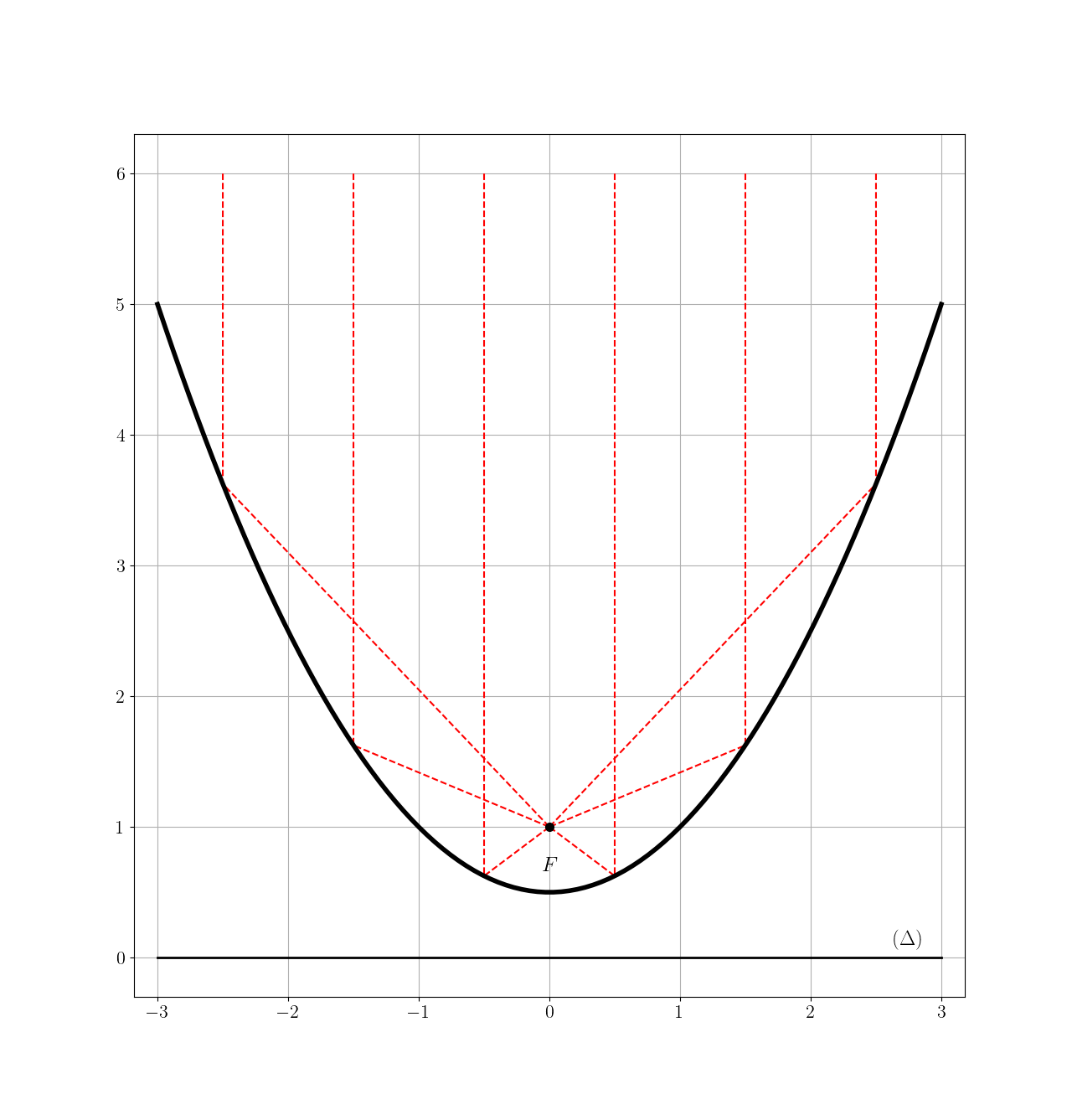
En revanche, cette condition n’est plus vérifiée dès lors que la source à l’infini n’est plus située sur l’axe optique mais arrive au télescope avec une incidence non-nulle, ainsi que l’illustre la petite animation ci-dessous.

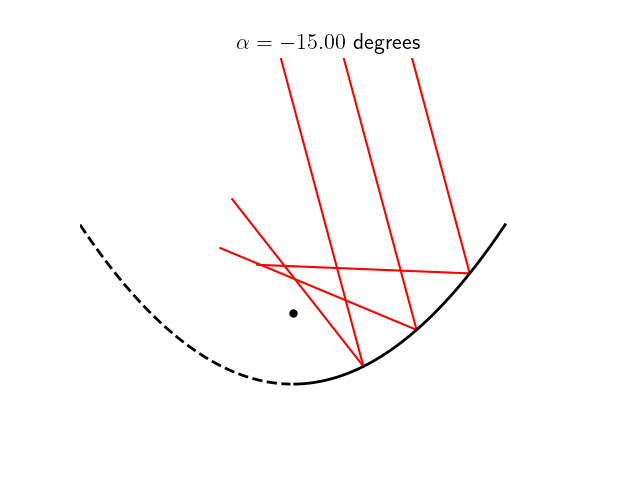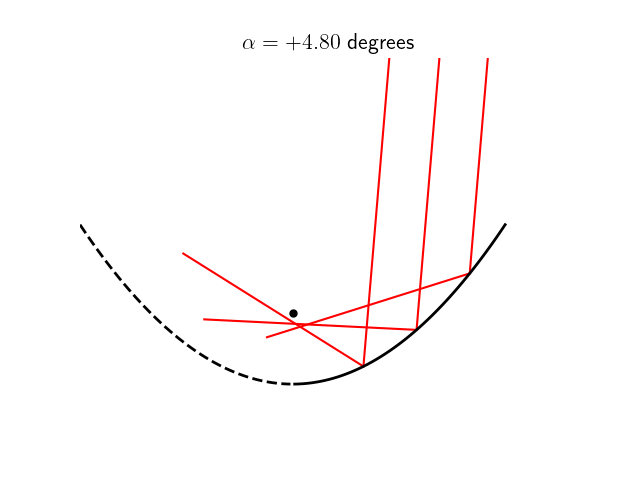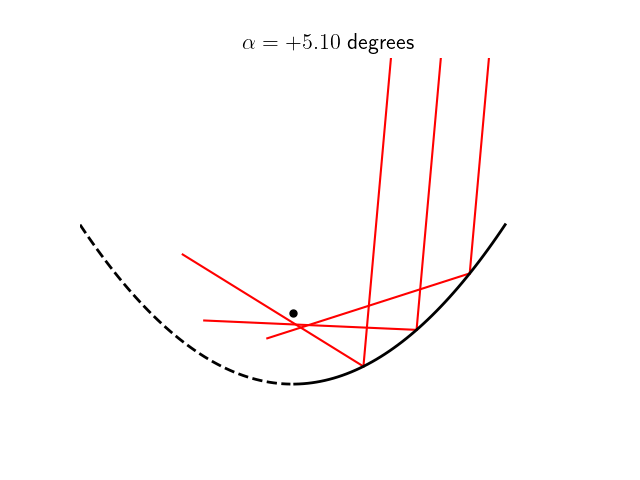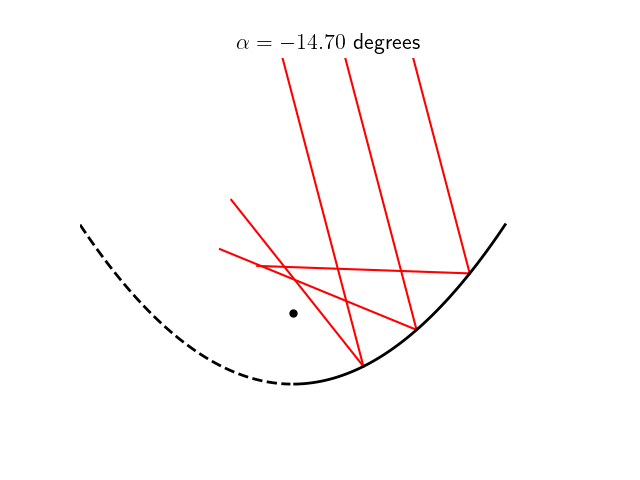
Dans les conditions de Gauss, on peut approximer la surface parabolique par une sphère de rayon $r=2f$. Certains télescopes de mauvaise qualité utilisent à ce propos de véritable miroir sphérique, moins chers à produire mais produisant une aberration sphérique. Dans ce cas, les rayons d’une source à l’infini sur l’axe optique qui arriveraient sur le bord du miroir ne seront pas exactement renvoyés vers le foyer, comme on peut le constater sur cette animation ci-dessous. Plus la distance $d$ avec laquelle le rayon incident arrive sur le miroir est grande, plus le point $P$ image de $A$ sera éloigné de $F$.

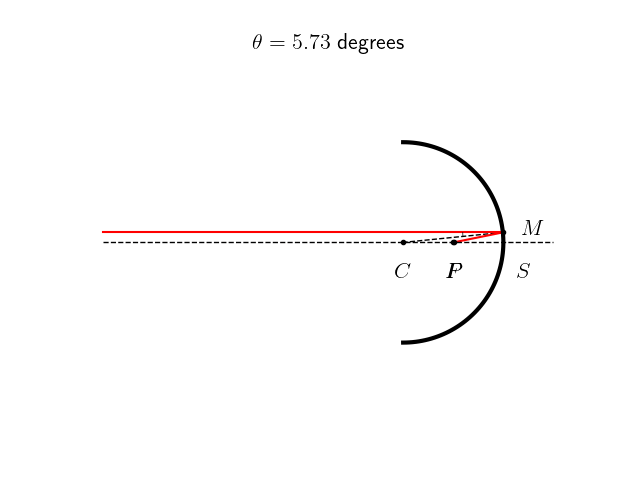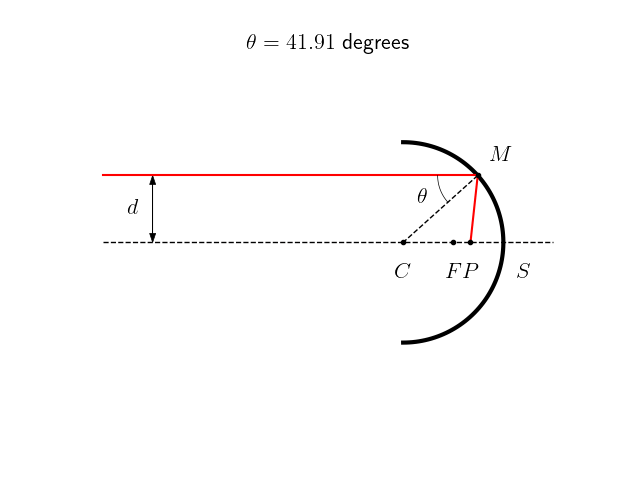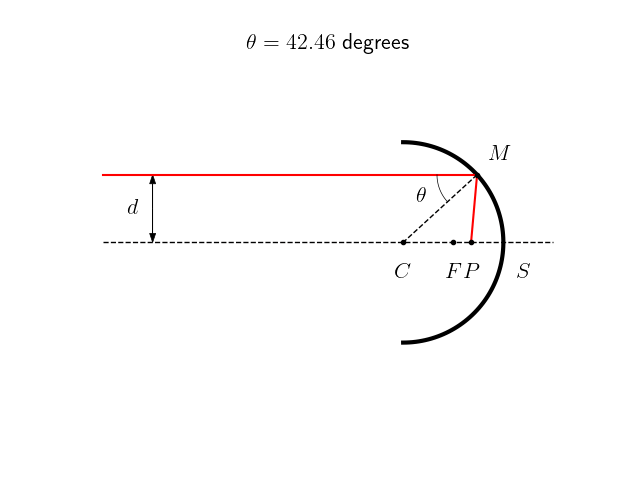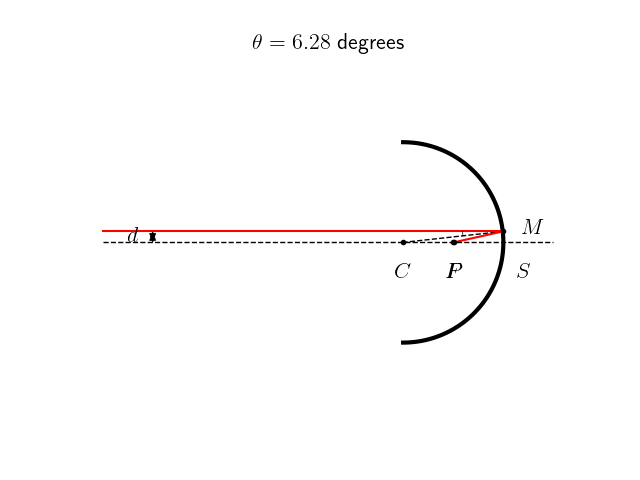
Si on note $S$ le sommet du miroir de rayon de courbure $r$, $P$ l’image de la source $A$ et $\theta$ l’angle de réflexion sur le miroir, alors le rapport $SP/r$ s’écrit formellement :

\[\frac{SP}{r} = \frac{1}{2 \cos \theta} -1\]

Ce défaut peut être corrigé grâce à une lame de Schmidt placée en amont du miroir.

Donc pour résumer les aberrations optiques des sources à l’infini:

• un miroir parabolique est rigoureusement stigmatique pour une source située sur l’axe optique à l’infini (incidence nulle)
• un miroir parabolique n’est pas stigmatique pour une source située à l’infini et arrivant avec une incidence non nulle
• un miroir sphérique n’est jamais rigoureusement stigmatique

Dans la suite, on se place dans l’approximation d’un miroir sphérique pour les équations de conjugaison. On supposera en outre que les sources observées seront toujours dans les conditions de Gauss, à savoir :

• les angles d’incidence sont petits devant le rayon de courbure du miroir
• les points d’incidence sont proches de l’axe optique, autrement dit la distance $d$ est petite devant le rayon de courbure du miroir : nous ne considérons que des rayons paraxiaux

Relation de conjugaison

La relation de conjugaison d’un miroir sphérique de rayon de courbure $r$ relie la position $p_2$ de l’image d’un point $p_1$ situé sur l’axe principal. Les distances sont algébriques et mesurées par rapport au sommet $S$ du miroir. Les calculs font apparaître deux points remarquables : le centre $C$ du miroir (situé à une distance algébrique de $r$ pour un miroir concave) et son foyer $F$ (située à une distance algébrique $f$ de $r/2$). Les quantités $p_1$ et $p_2$ sont reliées par l’équation de conjugaison suivante :

\[\frac{1}{p_2} + \frac{1}{p_1} = \frac{2}{r}\]

Soit en remarquant que $f=r/2$ :

\[\frac{1}{p_2} + \frac{1}{p_1} = \frac{1}{f}\]

Le grandissement transversal $\gamma$ du miroir sphérique s’écrit :

\[\gamma = \frac{-p_2}{\phantom{-}p_1}\]

Ce qui donne au final :

\[\gamma = \frac{r}{r-2 p_1}\]

L’animation ci-dessous représente l’évolution de l’image (en vert) pour un objet réel (en rouge) situé dans l’espace des $p$ négatifs (voir l’image en grand). La relation de conjugaison ($p_2$ en fonction de $p_1$) est tracée en bas à gauche et le grandissement $\gamma$ est tracé en bas à droite.

On remarque en particulier que l’image d’un objet placé dans le plan focal se retrouve projeté à l’infini. Ainsi lorsqu’on regarde sans oculaire et sans accomodation, on observe dans le télescope l’image de l’araignée et du miroir secondaire : c’est ainsi que se fait la collimation.

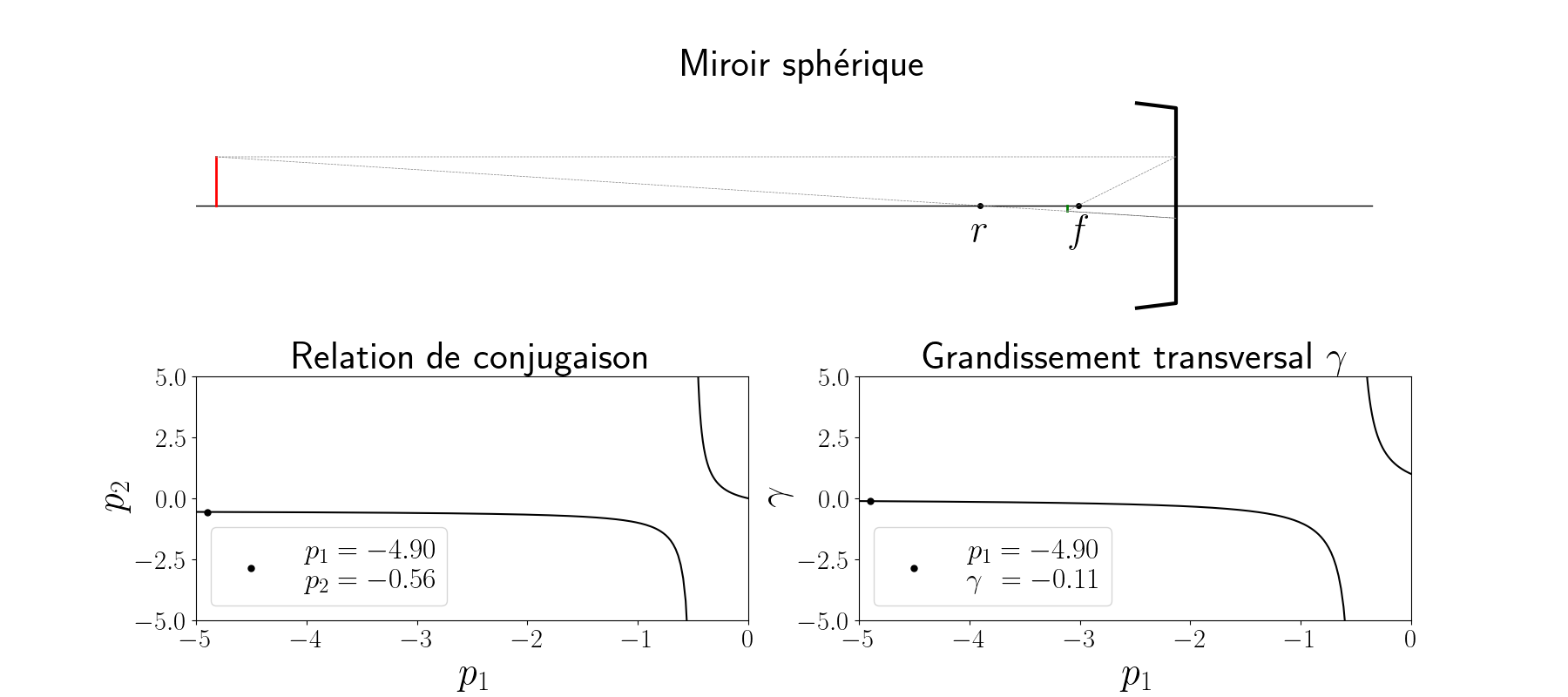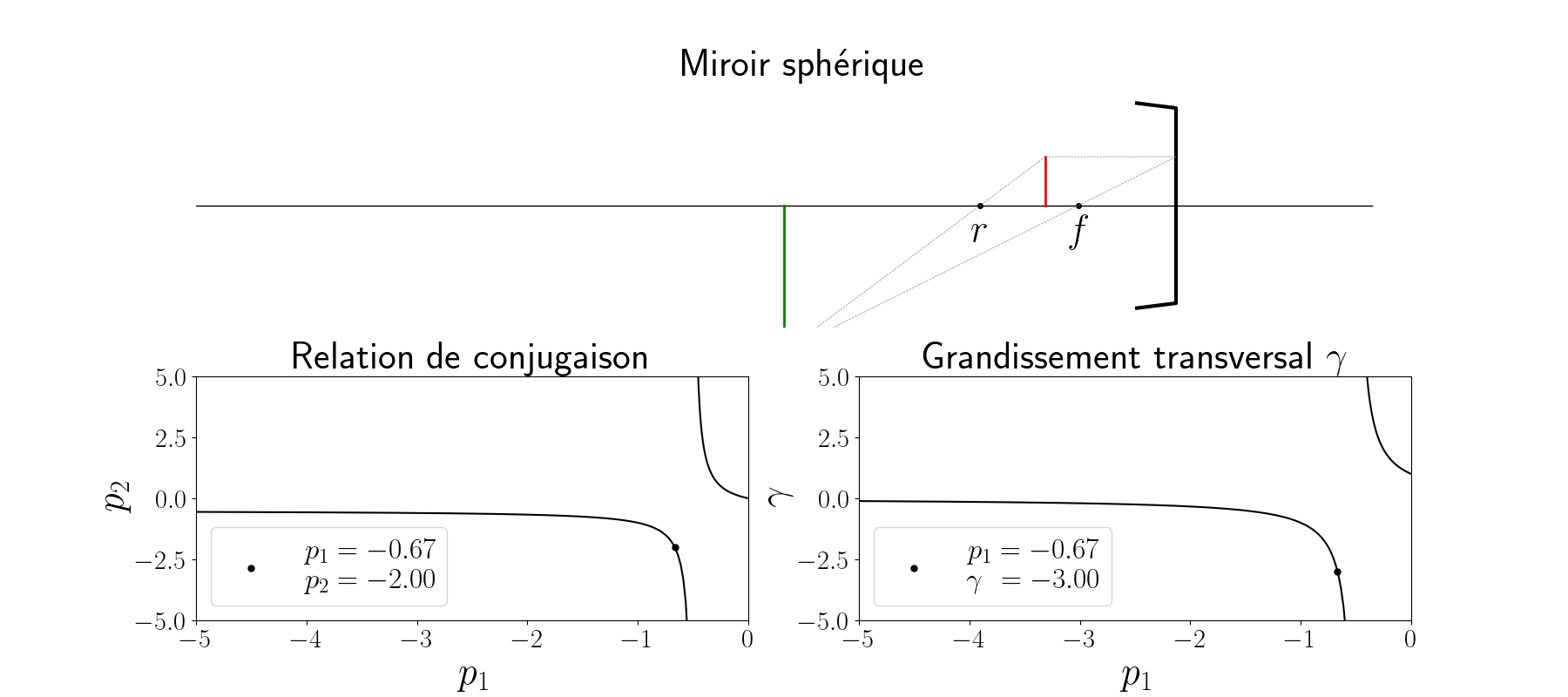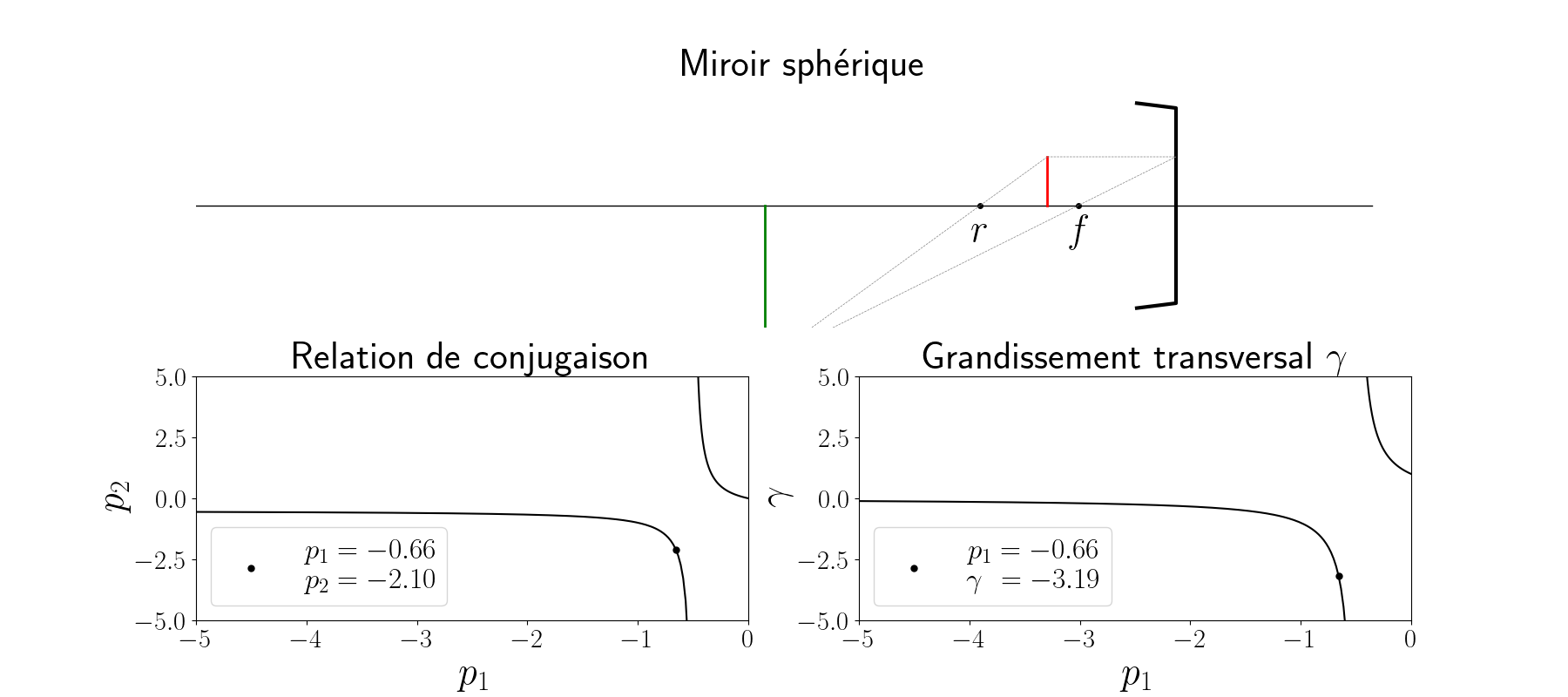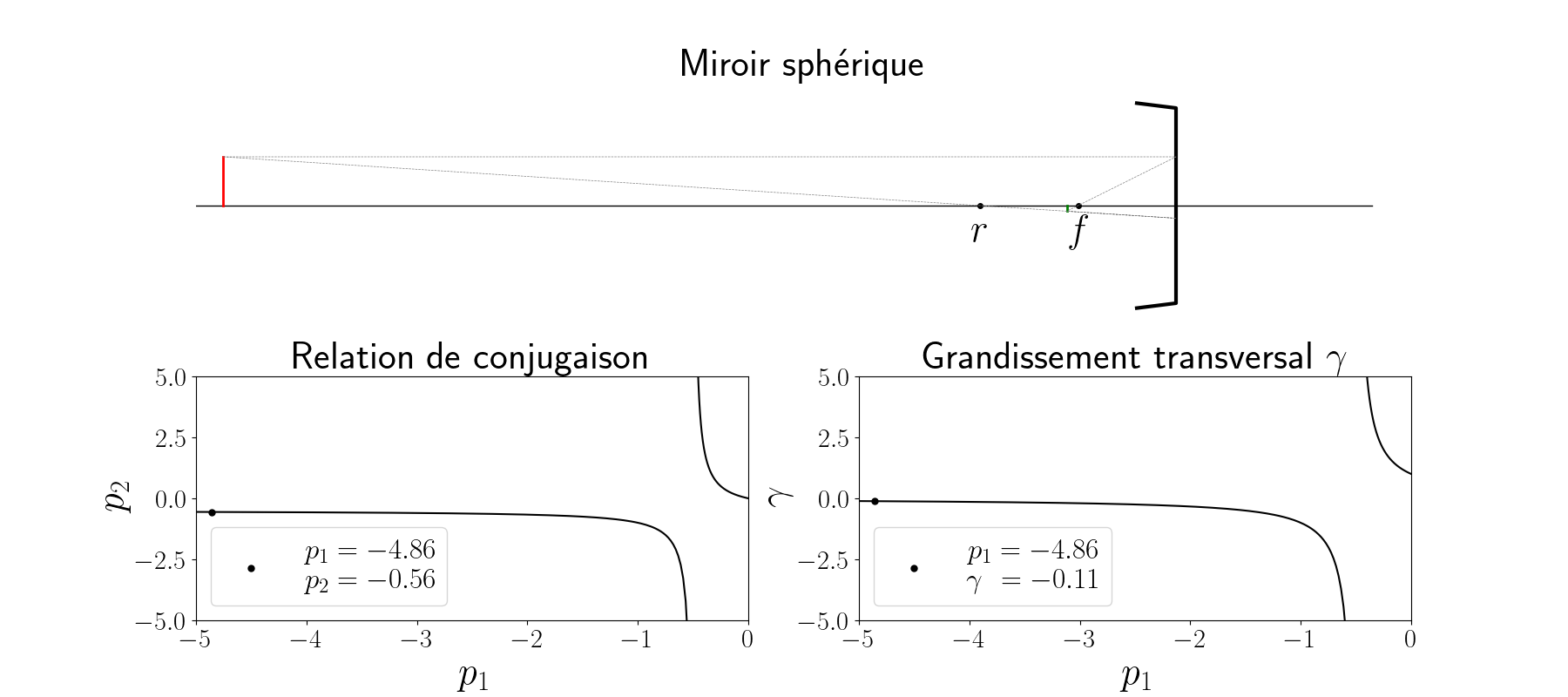
Dans la suite de l’étude, on se restreindra à l’étude de sources situées sur l’axe optique à une très grande distance $p_1$, c’est à dire $p_1 \to -\infty$. Dans ce cas, nous avons immédiatement $p_2 = r/2 = f$ : l’image d’un objet situé à l’infini sera bien dans le plan focal image du miroir.

Lorsqu’on traite d’objets situés à grande distance, on entend par là que $|p_1| \gg |r|$. Dans ce cas, on introduit le diamètre apparent $\alpha$. Cette quantité s’exprime en fonction de la taille $D$ de l’objet et de sa distance $p$ par rapport à l’observateur. On a ainsi :

\[\tan \frac{\alpha}{2} = \frac{D}{2p}\]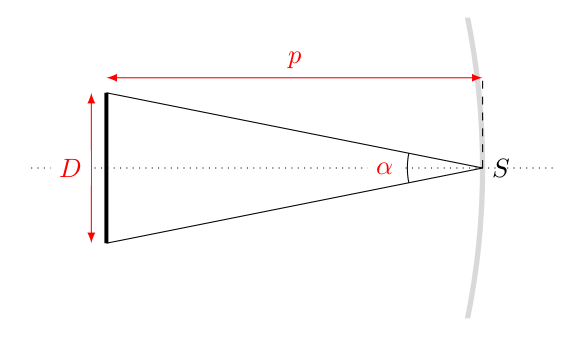

Lorsque l’ouverture angulaire est petite, on peut écrire :

\[\alpha \approx \frac{D}{p}\]

La taille algébrique $D’$ de l’image dans le plan foyer image s’écrira alors :

\[D' = -f \alpha\]

Le signe a son importance : l’image, dans un télescope de Newton, sera renversée. Plus précisement, cette image subit une symétrie centrale dont le centre est le foyer du miroir (on rappelle que l’image s’inscrit dans le plan focal).

Voici ci-dessous quelques ordres de grandeur pour différents objets du ciel. Concernant le diamètre $D’$, nous avons choisi une longueur focale de 1 mètre. Dans le cas des planètes, les distances avec la Terre sont données dans le cas le plus favorable (min) ou le cas le pire (max). On indique également la magnitude apparente dans le cas le plus favorable.

Nom	Type	Distance $p$	Diamètre $D$	Angle apparent $\alpha$	Diamètre $D’$	Magnitude apparente
Lune	planétaire	384 400 km	3478.8 km	0.5°	1 cm	-12.6
Mars	planétaire	0.3 ua ~ 2.7 ua	6779.0 km	25” ~ 3”	0.1 mm ~ 16 μm	-2.9
Jupiter	planétaire	3.9 ua ~ 6.5 ua	139 822 km	49” ~ 29”	0.24 mm ~ 0.14 mm	-2.9
Saturne	planétaire	8.0 ua ~ 11 ua	116 464 km	20.1” ~ 14.5”	100 μm ~ 70 μm	0.4
Galaxie d’Andromède	ciel profond	778 kpc	140 000 al	3°	5 cm	3.4

C’est en étudiant ce tableau qu’on se rend compte que le choix d’un télescope est un compromis :

• les objets planétaires ont une luminosité importante mais un angle apparent petit : il faut les grossir au maximum pour pouvoir les observer dans de bonnes conditions,
• les objets du ciel profond sont peu lumineux et étendu : trop les grossir les rendra flous et tronqués

Le miroir secondaire

Le miroir secondaire permet simplement de déporter la position de l’oculaire sur le côté du télescope. On le supposera plan, ce qui est je crois le cas dans tous les télescopes de Newton¹.

Compte-tenu de sa planarité, ce miroir n’interviendra donc pas dans le bilan des relations de conjugaison. En revanche, il pourra avoir son influence si on considère son éventuelle contribution dans le calcul de la pupille de sortie. Dans ce cas il est nécessaire de calculer quel est l’élément limitant du montage optique et ce calcul fait intervenir les dimensions de chaque élément. J’ai l’impression que le rayon du miroir secondaire est d’environ 10% de celui du miroir primaire.

Afin de déporter l’axe optique à 90° sur le côté du télescope, il est nécessaire d’incliner le miroir secondaire à 45° par rapport à l’axe optique initial. Afin de ne pas introduire d’anisotropie dans la collecte de la lumière, ce miroir doit présenter une section efficace parfaitement circulaire. On montre facilement que sa forme sera nécessairement une ellipse d’excentricité $1/\sqrt{2}$. La longueur de son demi-grand axe $a$ sera judicieusement choisie selon le compromis suivant :

1. d’une part, on souhaite conserver le maximum d’information des objets quasi-situés à l’infini et qui auront une étendu spatiale donnée dans le plan focal image du miroir primaire : ceci nous incite à choisir le miroir secondaire le plus grand possible
2. d’autre part, on souhaite minimiser la perte de luminosité introduite par l’obturation du miroir primaire par le secondaire : ceci nous incite à choisir le miroir secondaire le plus petit possible

L’oculaire de sortie

L’oculaire de sortie est généralement une association de lentilles qu’on peut réduire à une unique lentille mince convergente. Les propriétés importantes sont les suivantes :

1. sa vergence $\Phi$ qui est inversement proportionnelle à la distance focale image,
2. son champ de vision, exprimé en degrés,
3. son coulant, c’est-à-dire le diamètre de l’oculaire exprimé en pouces ou en mm, ce dernier pourra intervenir dans le calcul de la pupille de sortie et pourra limiter le champ apparent,
4. les éventuelles corrections d’aberration, que permet une association de lentilles judicieusement choisies (on pensera par exemple à l’oculaire achromatique de Huygens qui compense l’aberration chromatique d’une lunette)

Dans le cas d’une lentille mince, la vergence $\Phi$ est directement liée à l’indice de réfraction $n$ et aux rayons de courbure algébrique entrant et sortant $r_1$ et $r_2$, selon la relation suivante :

\[\Phi = (n-1) \left( \frac{1}{r_1} - \frac{1}{r_2}\right)\]

De façon analogue au miroir sphérique, les positions de l’objet $p_1$ et de l’image $p_2$ sont liés par la relation de conjugaison suivante :

\[\frac{1}{p_2} - \frac{1}{p_1} = \Phi\]

Ond définit également le grandissement transversal $\gamma$ de la lentille en fonction de $p_1$. Il s’exprime simplement comme le rapport $p_2/p_1$ et vaut donc :

\[\gamma = \frac{1}{1+p_1 \Phi}\]

Cette fois-ci la lentille va observer des objets situés dans son plan focal objet, il n’est dont pas pertinent de définir le grossissement de l’oculaire.

La figure animée ci-dessous illustre le principe de la lentille convergente (voir l’image en grand). Un mobile de hauteur fixe (en rouge), perpendiculaire à l’axe optique, se déplace selon ce dernier de la gauche vers la droite. On construit son image (en vert) par une lentille convergente de vergence $\Phi$, de foyer objet $f_1$ et de foyer image $f_2 = -f_1$. En bas à gauche est représenté la relation de conjugaison $p2(p_1)$ tandis qu’en bas à droite est tracé l’évolution du grandissement $\gamma(p_1)$

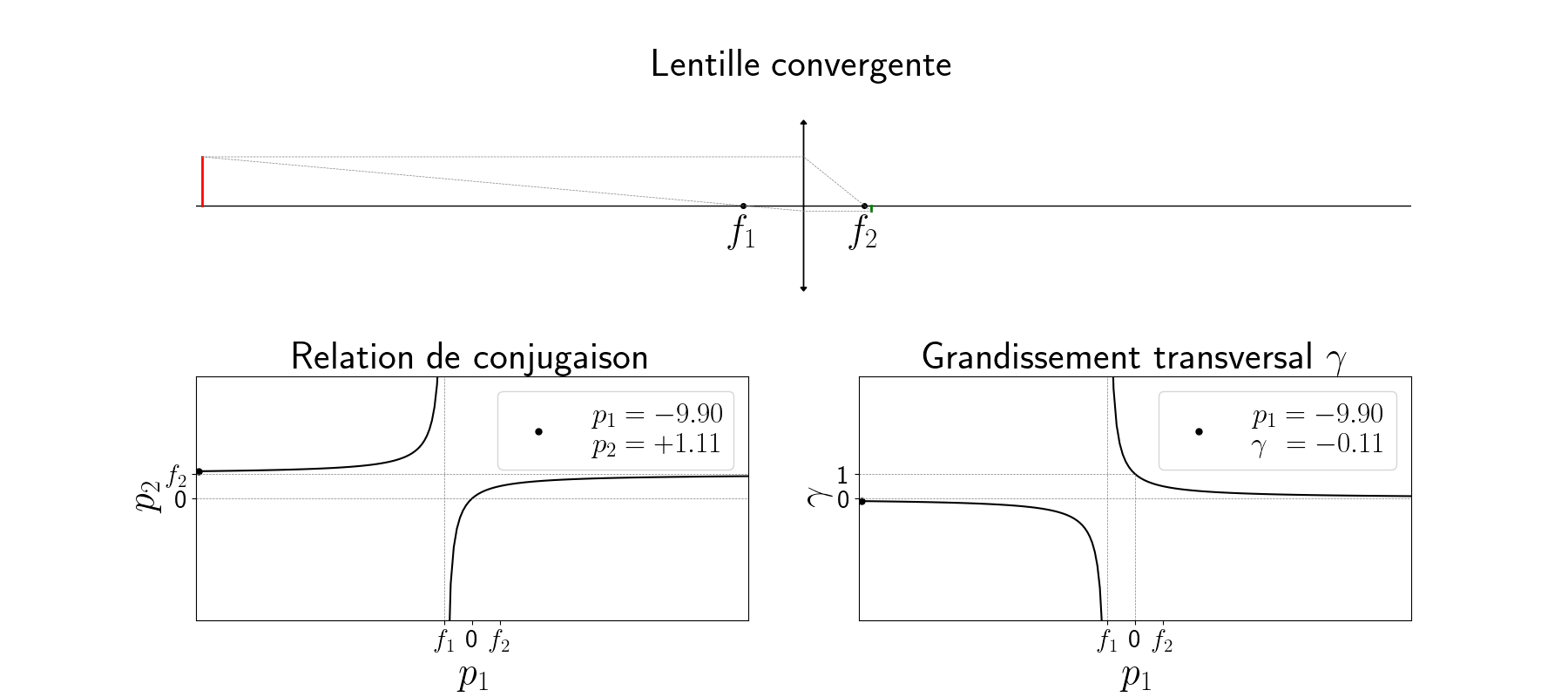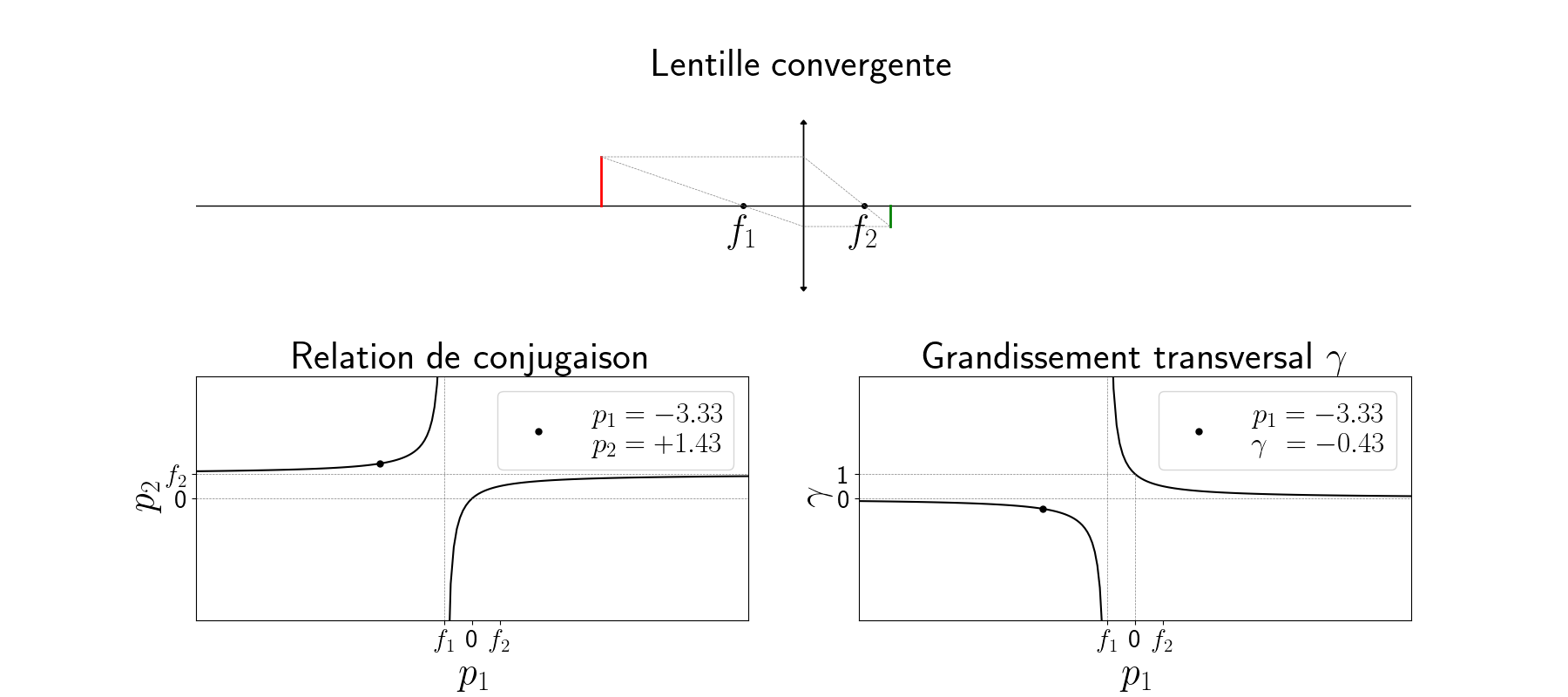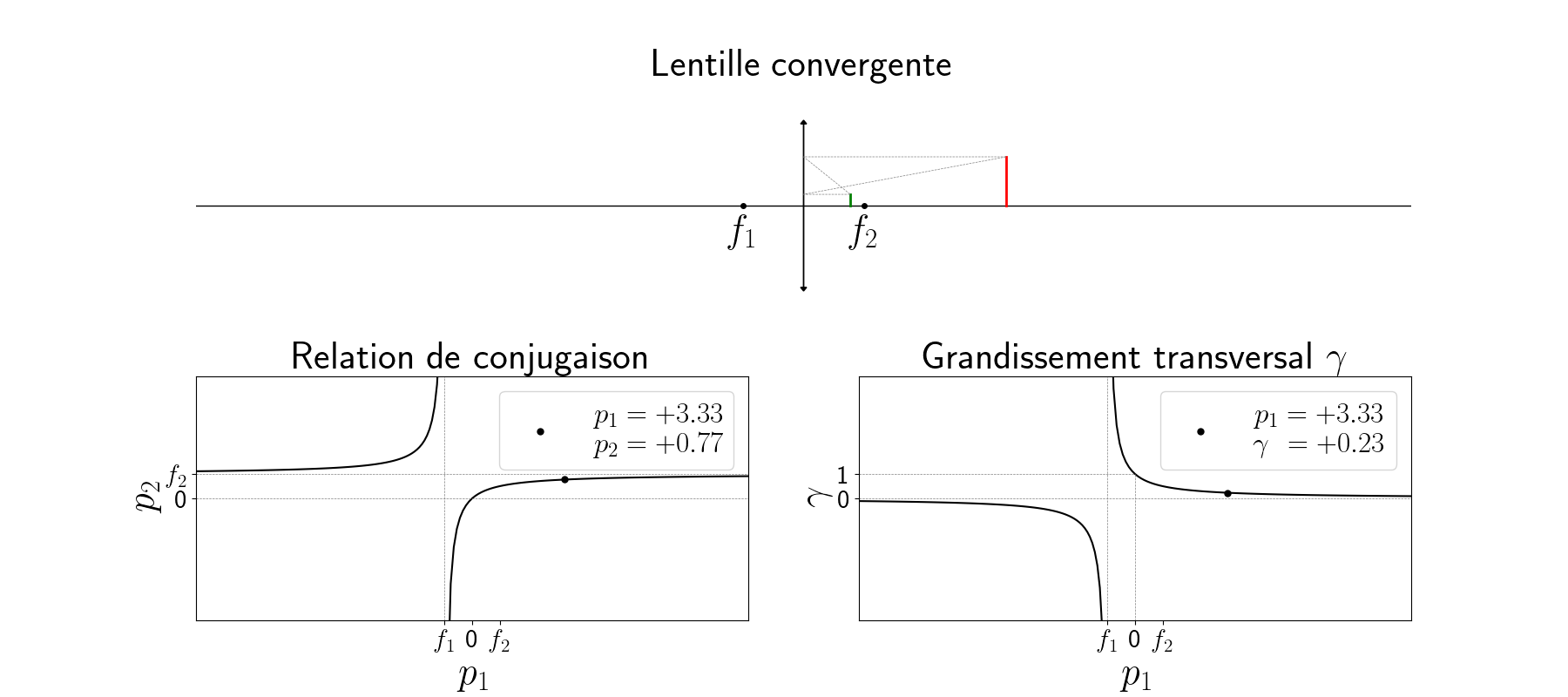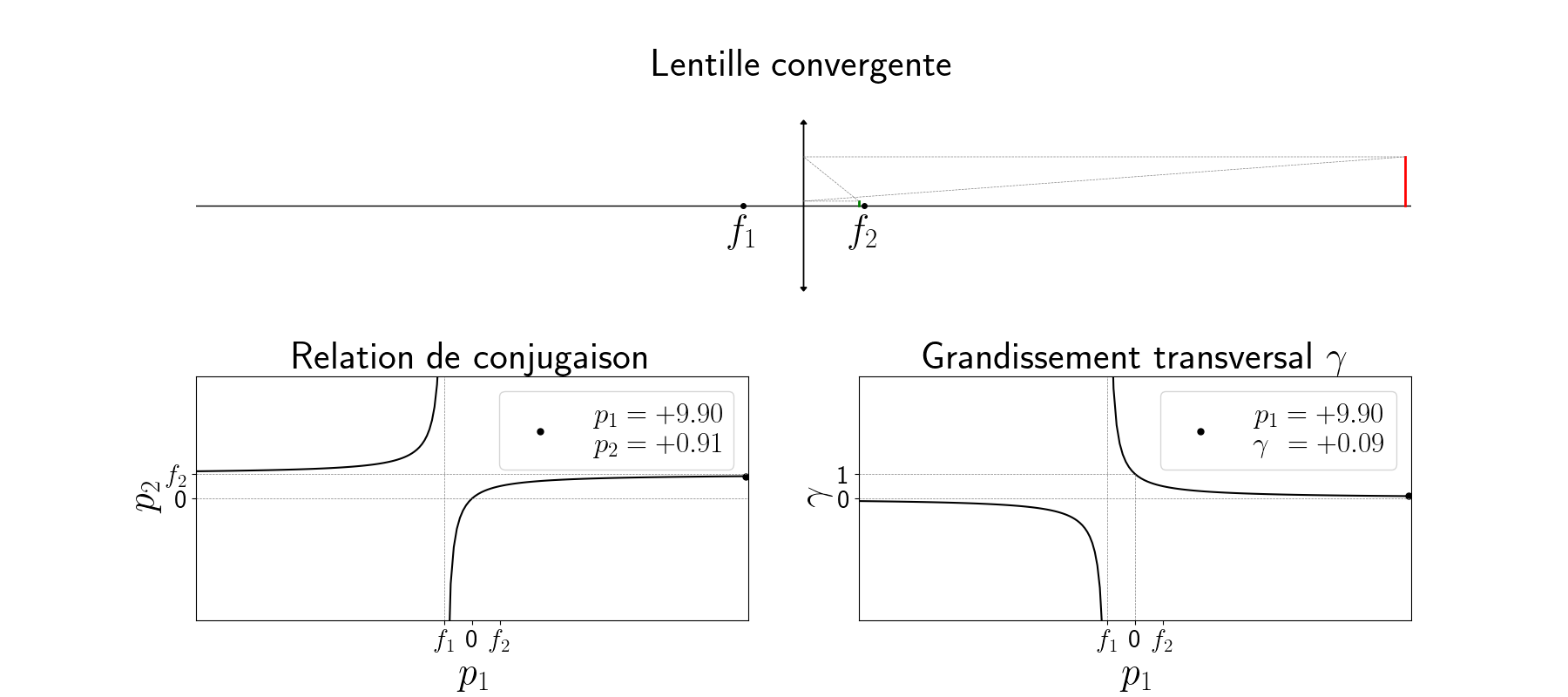
Fonctionnement nominal du télescope

On suppose qu’on fonctionne uniquement en mode afocal : c’est-à-dire que les foyers du système optique total sont rejetés à l’infini. Ainsi l’image d’une source lointaine sera elle aussi rejetée à l’infini : l’oeil pourra l’observer sans accomodation.

Ceci s’effectue simplement en réglant la mise au point de l’oculaire pour faire coïncinder le plan focal image du miroir principal avec le plan focal objet de l’oculaire.

Grossissement

Dans ces conditions d’observation, la première chose à calculer est le grossissement du télescope. Comme nous l’avons vu précedemment, un objet de dimension $D$ et situé à grande distance $p$ du miroir principal sera vu avec un angle apparent $\alpha \approx D/p$

L’image de cet objet sera dans le plan focal image du miroir principal et occupera une taille de $D’ = -f_1 \alpha$.

Dans l’hypothèse du montage afocal, ce nouvel objet sera vu en sortie d’oculaire avec un angle apparent $\alpha’ \approx D’/f_2 = -f_1 / f_2 \cdot \alpha$

Nous définissons le grossissement $G$ par la relation suivante :

\[G = \frac{\alpha'}{\alpha} = -\frac{f_1}{f_2}\]

Exemple : avec un miroir principal de focale 1000 mm et un oculaire de 10 mm, nous obtenons un grossisement $G=-100$. Le signe indique que l’image sera renversée.

Champ réel

Le champ est la portion d’espace dont l’instrument forme l’image. En général le champ de vision $\alpha_0$ de l’oculaire va limiter les valeurs pouvant être prises par l’angle $\alpha’$. En remontant la relation établie ci-dessus et liant $\alpha$ à $\alpha’$, nous obtenons l’équation du champ réel qu’on observera à travers l’oculaire :

\[\alpha \leq \frac{\alpha_0}{|G|}\]

Ainsi avec un télescope dont le grossissement est égal à 100 et avec un oculaire de 30° de champ, on observe un champ réel de 18 minutes d’arc. La Lune, qui occupe rappelons-le, un champ de un demi-degré, ne sera pas visible en entier dans ces conditions.

Disque oculaire

Le disque oculaire est l’image du miroir sphérique par l’oculaire. Placé généralement un peu en sortie de l’oculaire, ce disque représente la zone où le faisceau lumineux est le plus concentré : c’est idéalement à cet endroit là qu’il faudra placer son oeil.

Calculons la distance $p_2$ de ce disque ainsi que son diamètre $D_2$, dans le cas d’un objectif de diamètre $D_1$. Le système étant afocal, on sait que le miroir sphérique est situé à une distance $p_1 = f1+f_2$ du centre $S_2$ de l’oculaire. Notez bien que la quantité $p_1$ est ici négative puisque objectif et oculaire étant convergents, leur distance focale objet sont négatives. La relation de conjugaison de l’oculaire étudié ci-dessus nous donne immédiatement :

\[p_2 = \frac{p_1 f'_2}{p_1+f'_2}\] \[D_2 = |\gamma| D_1 = \left|\frac{p_2}{p_1}\right| D_1 = \left|\frac{f'_2}{p_1+f'_2}\right| D_1\]

La figure ci-dessous illustre l’évolution des caractéristiques du disque oculaire en fonction de la focale de l’oculaire pour un télescope de diamètre 200 mm et de distance focale primaire de 1 m. N’oublions pas que plus la focale est courte, plus la vergence est élevée.

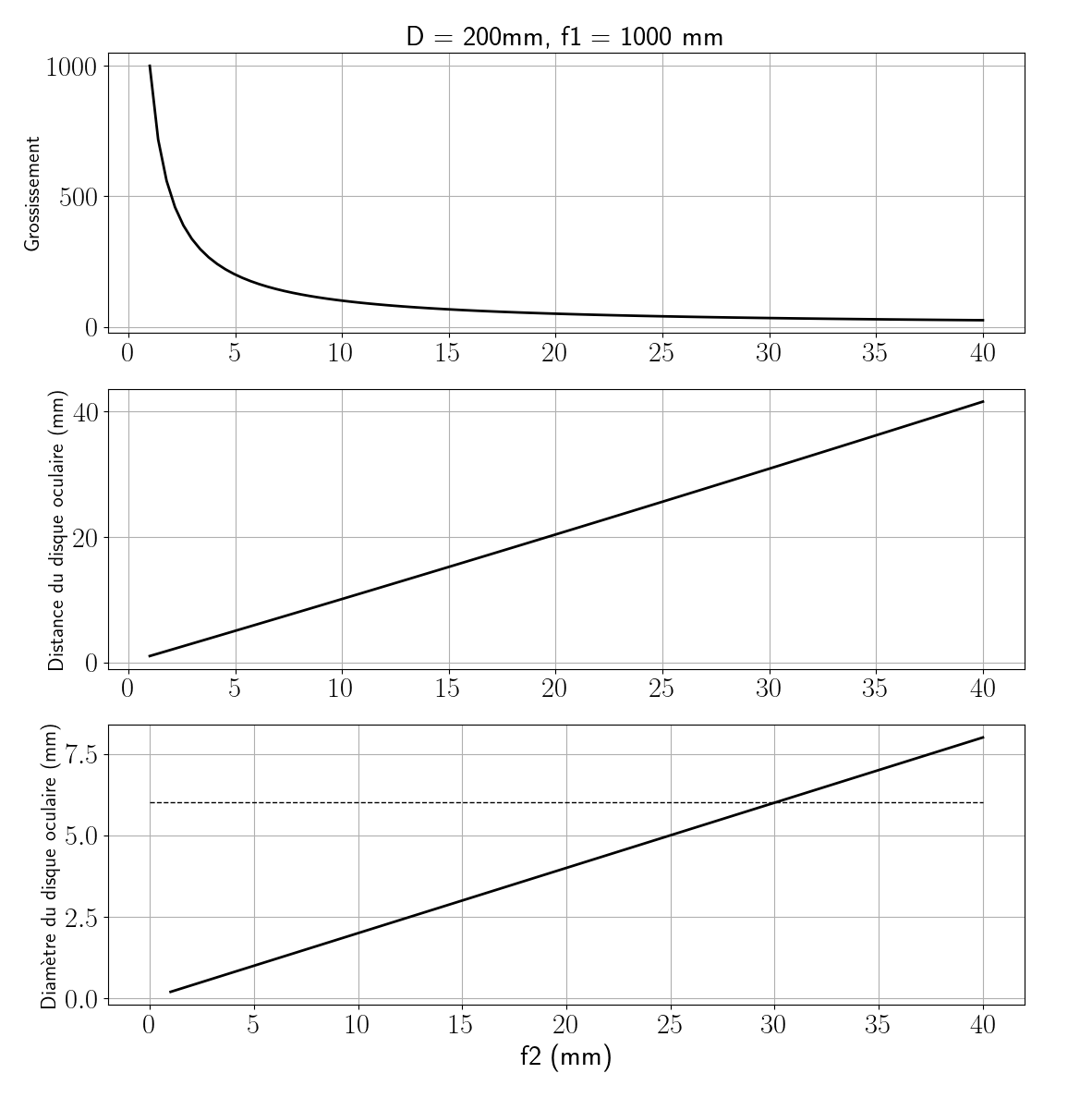
La courbe du haut représente la valeur absolue du grossissement en fonction de $f_2$. On remarque que les plus courtes focales d’oculaire conduiront aux plus forts grossissement.

La courbe du milieu représente l’évolution en fonction de $f_2$ de la distance $p_2$. Cette distance est mesurée algébriquement par rapport au centre $S_2$ de la lentille équivalent de l’oculaire et n’a de sens que si l’on sait précisément situer ce dernier. On constate que plus la focale de l’oculaire est courte, plus l’oeil devra être proche de l’oculaire.

Plus intéressant, la courbe du bas représente l’évolution du diamètre du disque oculaire $D_2$. Idéalement, on souhaite que ce dernier fasse exactement la taille de la pupille (typiquement environ 6 mm). Lorsque cette condition est exactement réalisée, on dit que nous sommes dans les conditions de grossissement équipupillaire. Il est representé sur la figure par un trait en pointillé et correspond ici à une focale d’oculaire de $f_e = 30 mm$, le grossissement est alors $G_e = - f_1/f_e$.

D’une façon générale, nous avons :

\[f_e = \frac{6 \textrm{mm}}{D_1} f_1\] \[G_e = \frac{-D_1}{6 \textrm{mm}}\]

Si nous utilisons un oculaire de focale plus élevée que $f_e$ alors simultanément :

1. notre grossissement diminue,
2. notre champ réel augmente,
3. la luminosité globale de l’image diminue (puisque une partie de la lumière du cercle oculaire n’entrera plus dans la pupille).

De la même façon, si nous utilisons un oculaire de focale plus faible que $f_e$ alors dans ce cas :

1. notre grossissement augmente,
2. notre champ réel diminue.

Il est d’usage de ne pas descendre en-deça du grossissement équipupillaire car alors les performances de l’instrument chutent. Réciproquement, et de façon empirique, il est généralement convenu que le grossissement maximal d’un télescope ne doit pas dépasser $2 D_1$ (avec $D_1$ exprimé en mm). Pour un miroir de 200 mm, le grossissement maximal ne devrait ainsi pas dépasser 400.

Photométrie énergétique

Soit un objet lumineux du ciel rayonnant avec une puissance lumineuse $\Phi$² qui s’exprime en Watt. A une distance $d$ de cet objet et dans l’hypothèse d’un rayonnement isotrope, cette énergie se trouve uniformément répartie sur une sphère de rayon $d$. Nous définissons l’éclairement $E$, exprimé en $W/m^2$, par :

\[E = \frac{\Phi}{4 \pi d^2}\]

On l’a vu, si cet objet a un diamètre $\delta$, son image dans le plan focal image du miroir primaire du télescope de diamètre $D_1$ et de focale $f_1$ aura un diamètre $\delta’$ qui s’écrira :

\[\delta' = \frac{-f_1}{d} \cdot \delta\]

Cette image possède également un éclairement $E’$ dont l’expression fait intervenir l’éclairement initial $E$, la surface $S_1$ du miroir primaire et la surface $S$ de l’image. Nous avons :

\[E' = E \frac{S_1}{S}\]

En remplaçant les expressions, il vient rapidement :

\[E' = \frac{\Phi}{4 \pi} \left( \frac{D}{f_1 \delta} \right)^2\]

Illustrons ce dernier résultat par le cas de la Lune. Cette dernière émet une puissance lumineuse $\Phi = 2.7 \cdot 10^{15} \textrm{W}$. Son diamètre $\delta$ vaut 3300 km et la distance Terre-Lune moyenne $d$ vaut 384 000 km. Avec un télescope possédant un miroir primaire de 200 mm, voici comment évoluent en fonction de la focale du primaire la taille de l’image (en cm, en haut) et l’éclairement de l’image (en $\textrm{W}/\textrm{m}^2$, en bas).

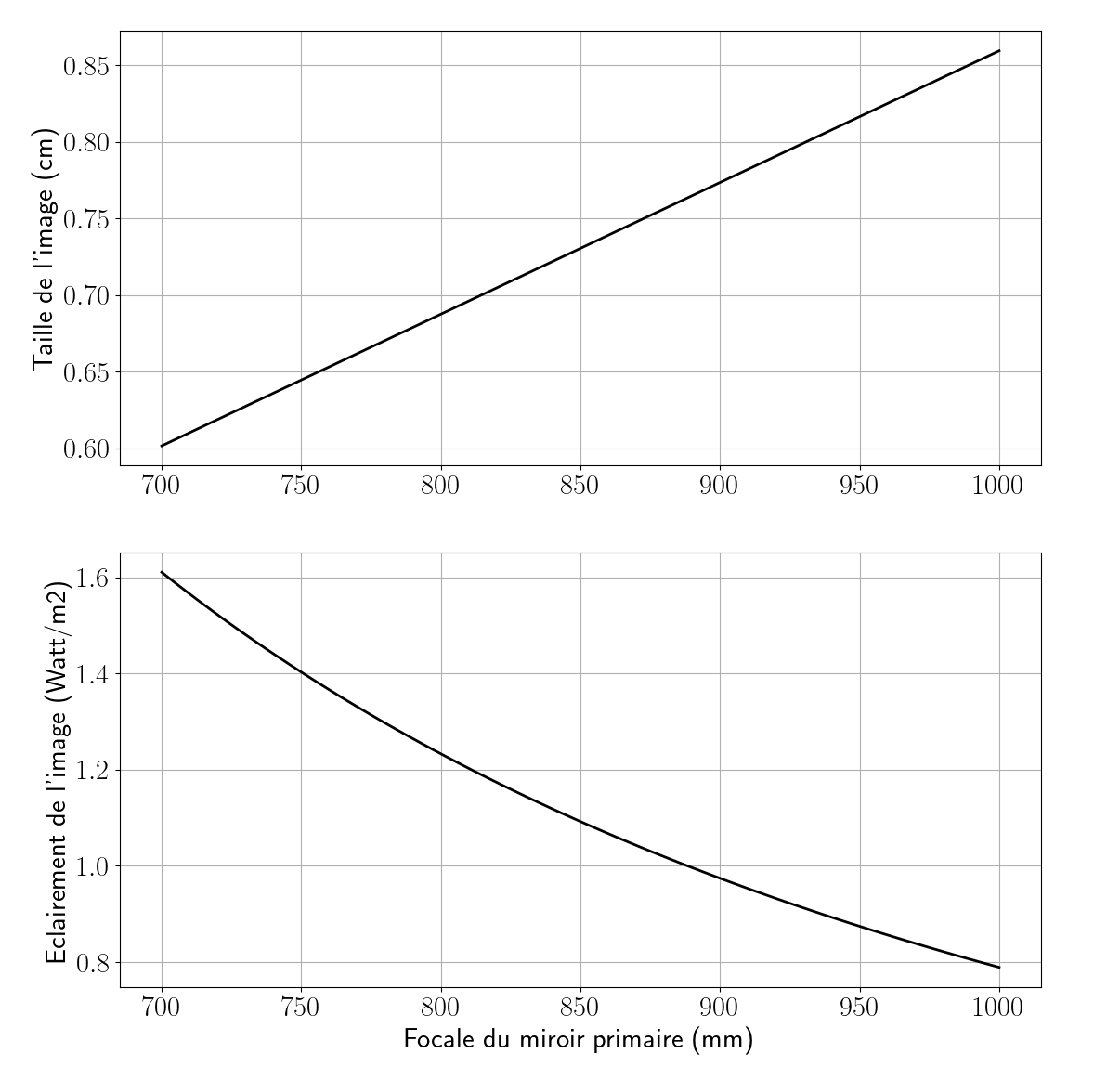
On observe immédiatement que plus la focale du primaire augmente, plus l’objet sera étendu et moins il sera lumineux. C’est un point clef de l’astrophotographie puisque les photosites de l’appareil seront placés, il me semble, dans le plan focal du miroir primaire. Le couple télescope / appareil photo ne fonctionne plus en afocal et ce sont les caractéristiques de l’image par le primaire qui seront importantes.

Pour la photographie planétaire, les objets étant très lumineux, il n’est pas grave de perdre en luminosité. En revanche on veut pouvoir accéder facilement à de forts rapports $f_1/f_2$ (le grossissement). C’est pourquoi on a tendance à privilégier les instruments dont le miroir principal possède une longue focale.

Pour la photographie du ciel profond, c’est l’inverse : on veut à tout prix avoir l’instrument le plus lumineux possible. La quête du plus fort grossissement est moins critique (on préfère avoir un grand champ). On se rabattra alors de préférence vers des instruments à courte focale. Bien entendu, l’image sera alors d’autant plus petite et occupera une toute petite zone de la surface sensible de l’appareil photo : on perdra alors un peu en résolution.

Les raisonnements présentés ici ont accordé une très grande importance aux caractéristiques de l’image par le miroir primaire (taille et éclairement). Ceci est critique en astrophotographie mais n’intervient pas dans le cas d’une observation directe puisqu’on fonctionne de nouveau en afocal.

Un petit simulateur de télescope

J’ai mis sur mon GitHub une première ébauche de simulateur de télescope, toujours sous license GPL.

On renseigne dans un premier temps l’objet céleste qu’on souhaite observer. Pour le moment, seuls Mars, Jupiter, Saturne et la Lune sont accessibles, mais la liste peut facilement être étoffée car tout est défini dans un fichier JSON. On peut influer sur la distance entre l’astre et la Terre qui peut varier entre deux extrema. Pour simplifier, j’ai fait ici l’hypothèse d’orbites circulaires co-planaires car seul l’ordre de grandeur m’intéresse; mais on peut toujours envisager un raffinement de l’algorithme ici…

On définit ensuite les caractéristiques du télescope de Newton (diamètre du miroir primaire, longueurs focales primaire et secondaire, champ apparent).

Le programme met ensuite à jour tout un tas d’information dont on a donné la définition dans le corps de cet article. Seules les magnitudes apparentes me donnent encore un peu de soucis car il y a une constante ad-hoc à calculer et une simple règle de trois ne semble pas suffisante. Cela nécessite un peu de travail supplémentaire mais je n’ai plus trop de temps à y consacrer dans l’immédiat.

Voici par exemple, les paramètres associés à l’observation de la planète Mars par un télescope de 200 mm de diamètre.

Si l’utilisateur clique sur le bouton Plot, il obtient un visuel de ce qu’il pourrait s’attendre à voir dans un vrai télescope. Pour bien interpréter l’image, il est important de comprendre que le disque noir doit correspondre au champ apparent choisi par l’utilisateur (ici 52°). C’est donc à l’utilisateur de se placer correctement par rapport à cette image pour que le disque noir occupe environ 52° de son champ de vision.

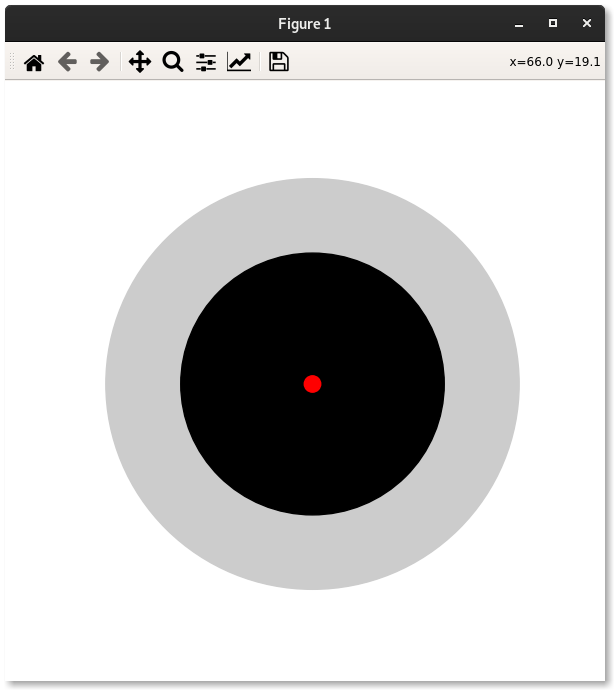
Je retrouve les mêmes résultats que le simulateur (simplifié) de Stelvision, ce qui est une bonne nouvelle. Il me reste toutefois à régler un certain nombre de problèmes mineurs et d’optimisation dont je donne le détail sur mon GitHub, mais je reste content de cette première version même si elle est imparfaite.

Ressources

Pas beaucoup de ressources ici. L’intégralité des formules présentées ici dérivent des lois de base de l’optique mises bout-à-bout.

“Cours de Physique, Optique”, de Jean-Paul Parisot, Patricia Segonds et Sylvie Le Boiteux, aux éditions Dunod. ISBN 978-2-10-081086-4.

1. ce ne sera en revanche pas le cas pour d’autres types de télescope. Les Schmidt-Cassegrain par exemple utilisent des miroirs secondaires convexes (généralement sphériques). Les Ritchey-Chrétien quant à eux utilisent des miroirs secondaires convexes hyperboliques. ↩

2. à ne pas confondre avec la vergence ! Mais le contexte ne le permet pas. ↩