Mon premier verger

J’ai récemment joué quelques partie du jeu de société “Mon Premier Verger” avec mes enfants (Marie 5 ans et Alice 2 ans). Nous avons gagné toutes les parties et je me suis demandé dans quelle mesure nous avons eu de la chance.

Rien ne semble plus simple que de dresser une liste, en fait c’est beaucoup plus compliqué que ça n’en a l’air : on oublie toujours quelque chose, on est tenté d’écrire etc., mais justement, un inventaire, c’est quand on n’écrit pas etc.

Georges Perec, Penser/Classer

• TL;DR
• Description du jeu
• Modélisation
  • Défaite en N coups
  • Victoire en N coups
  • Cas général
• Simulation de Monte-Carlo

TL;DR

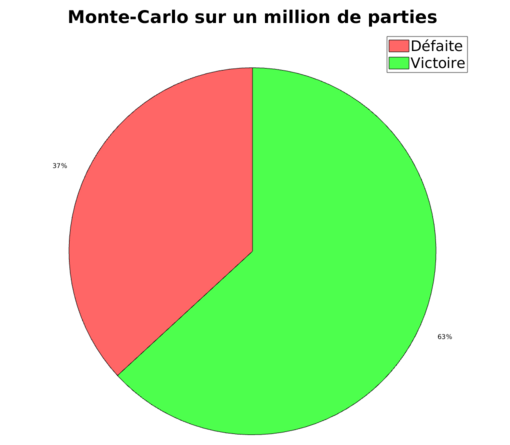
Une simulation de Monte-Carlo sur un million de partie montre que les joueurs gagnent dans 63% des cas.

Description du jeu

Ce jeu de société, édité par Haba, est un jeu collaboratif où le but est de cueillir tous les fruits du verger avant que le corbeau ne les mange.

Voici le descriptif donné par le dos de la boîte de jeu :

Dans le verger, les arbres fruitiers croulent sous les fruits. Attention à l’effronté corbeau Théo qui aimerait tous les dérober ! Suivant le symbole du dé, ramassez un fruit et placez-le dans votre panier ou faites avancer Théo sur le chemin vers le verger. Vous gagnerez tous ensemble si vous cueillez tous les fruits dans que Théo n’arrive dans le verge.

Il est indiqué que le jeu est dimensionné pour 1 à 4 joueurs à partir de deux ans et qu’une partie dure environ 10 minutes.

Le jeu se compose de :

• 4 tuiles arbres sur lesquels sont initialement posés 4 fruits en bois (4 pommes rouge sur le premier, 4 pommes vertes sur le deuxième, 4 poires jaune sur le troisième et enfin 4 prunes bleues sur le quatrième)
• un pion corbeau placé devant une piste de cinq cases
• un dé
• un panier

Le dé présente les six faces suivantes : Rouge, Vert, Jaune, Bleu, Panier et Corbeau.

Chacun à tour de rôle, les joueurs lancent le dé :

• si le résultat est Rouge, Vert, Jaune ou Bleu, le joueur doit retirer un fruit de la couleur du dé et le déposer dans le panier. S’il n’y a plus de fruit dans l’arbre, il ne se passe rien.
• si le résultat est Panier, le joueur choisit un fruit dans n’importe quel arbre et le dépose dans son panier
• si le résultat est Corbeau, le corbeau avance d’une case sur sa piste

Si les joueurs arrivent à cueillir tous les fruits avant que le corbeau n’atteigne la dernière case de sa piste, ils gagnent la partie tous ensemble.

Si le Corbeau arrive sur la dernière case de sa piste avant que tous les fruits n’aient pu être cueillis alors les joueurs perdent la partie tous ensemble.

Modélisation

Alors déjà, commençons par remarquer que ce jeu de société n’est pas un jeu normal au sens de Raymond Smullyan.

Dans son livre Satan, Cantor and Infinity¹, ce dernier considérait en effet comme normal tout jeu à deux joueurs se terminant en un nombre fini de coups. Ce concept fut introduit par le mathématicien William Zwicker pour pouvoir ensuite parler d’hyperjeu. Les réflexions autour de l’hyperjeu ont pu conduire à une démonstration inédite du théorème de Cantor qui stipule que le cardinal d’un ensemble $E$ est toujours strictement inférieur au cardinal de l’ensemble de ses parties $\mathcal{P}(E)$.

Dans le cas qui nous intéresse, les joueurs peuvent entrer dans un jeu sans fin où, comble de malchance, le dé tombe systématiquement sur la face bleue. La probabilité associée à cet événement est certes nulle mais la possibilité existe.

Alors, je tords un peu la définition originale car Raymond Smullyan ne parle aucunement de hasard. Par ailleurs, cela n’a aucune incidence sur la suite de nos développements. Alors je ferme là cette petite parenthèse mais je suis bien content d’avoir parlé de ce logicien dont j’avais dévoré les ouvrages étant lycéen.

Concernant la modélisation du jeu, on constate déjà que le nombre de joueurs importe peu puisqu’ils ont tous le même objectif et que leur marge de manoeuvre est très faible. Le seul degré de liberté dont ils disposent est de choisir la couleur du fruit lorsque le dé tombe sur la face Panier. La solution la plus rationnelle est alors de dépeupler l’arbre le plus fourni, et de choisir aléatoirement en cas d’égalité.

Nous supposons le dé parfaitement équilibré. A chaque tour, une des six faces est susceptible de sortir avec une probabilité de $1/6$. Voyons déjà ce que nous pouvons en tirer

Défaite en N coups

Dans un premier temps, nous ne prenons pas en compte les mécanismes susceptibles de faire gagner les joueurs et nous nous concentrons sur le Corbeau.

Soit $F(N)$ la probabilité que le Corbeau gagne en exactement $N$ coups.

Comme il faut que la face Corbeau sorte cinq fois pour gagner, nous avons déjà trivialement $F(1) = F(2) = F(3) = F(4) = 0$.

Pour gagner en exactement 5 coups, il faut que le Corbeau soit sorti systématiquement lors des 5 premiers coups. Les lancés étant indépendant, nous avons donc :

\[F(5) = \frac{1}{6^5}\]

De façon générale, la probabilité que le Corbeau gagne en $N$ coups s’écrit :

\[F(N) = \frac{\Omega_F (N)}{\Omega}\]

Ici $\Omega$ représente l’ensemble des configurations accessibles après $N$ lancés de dé. Nous avons donc $\Omega = 6^N$.

$\Omega_F (N)$ représente l’ensemble des configurations pour lesquelles le Corbeau gagne en exactement $N$ coups. Un peu de combinatoire nous donne :

\[\Omega_F (N) = {N-1 \choose 4} \cdot 5^{N-5}\]

Dans cette équation le terme $n \choose k$ représente le coefficient binomial classique, il correspond ici au nombre de façons différentes d’avoir tiré $5-1=4$ Corbeaux lors des $N-1$ tours précédents. C’est trivialement un cas d’application de loi binomiale de paramètres $p=1/6$ et $n = N-1$ avec la condition supplémentaire que le Nème lancé soit exactement un Corbeau.

La probabilité que le Corbeau gagne en exactement $N$ coups s’écrit finalement :

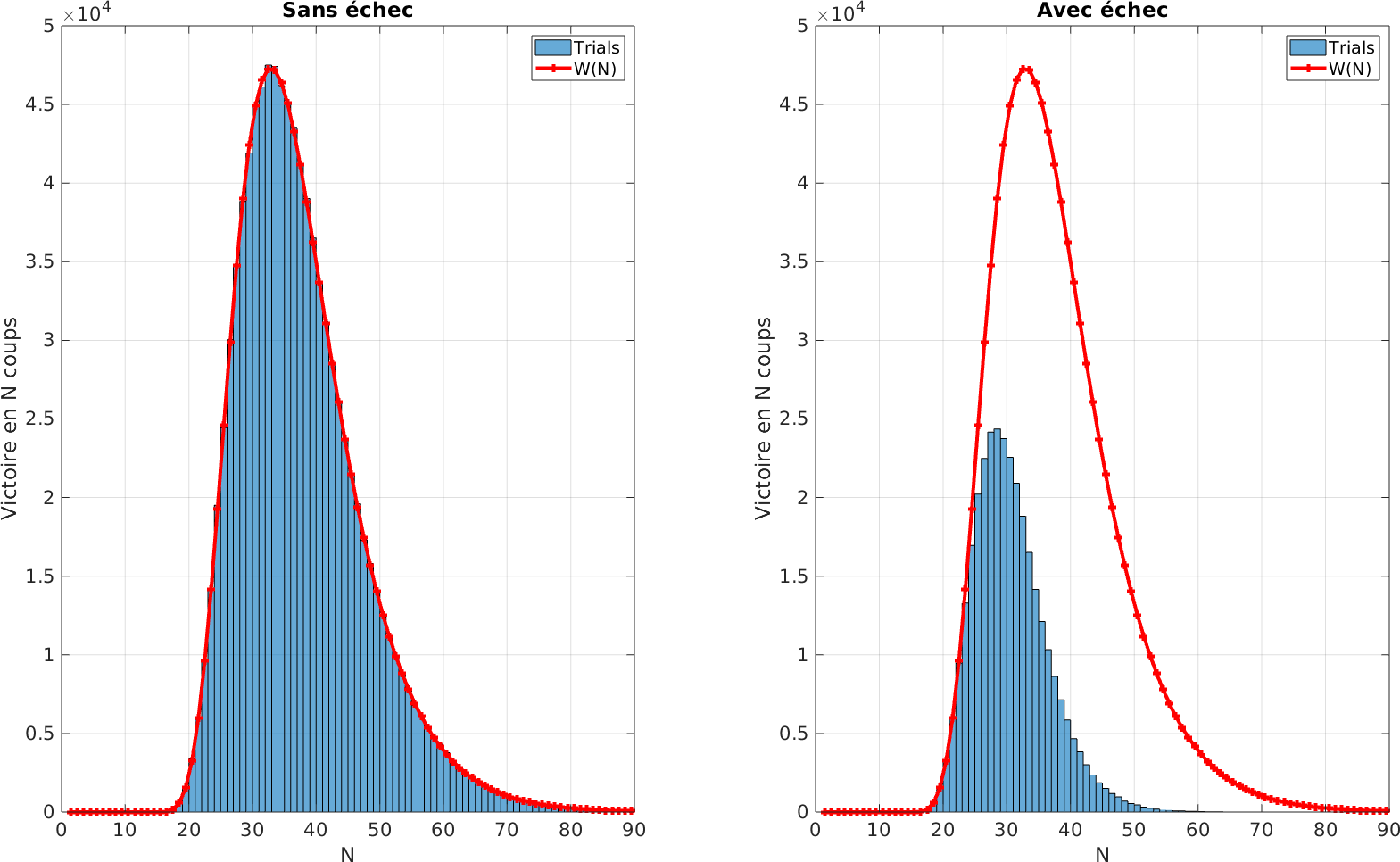
\[F(N) = {N-1 \choose 4} \cdot \frac{5^{N-5}}{6^N}\]

En pratique, si nous simulons la mécanique du Corbeau sur un million de parties successives, nous avons une parfaite adéquation entre notre fonction $F(N)$ et l’histrogramme des victoires du Corbeau, ainsi que l’illustre la figure ci-dessous.

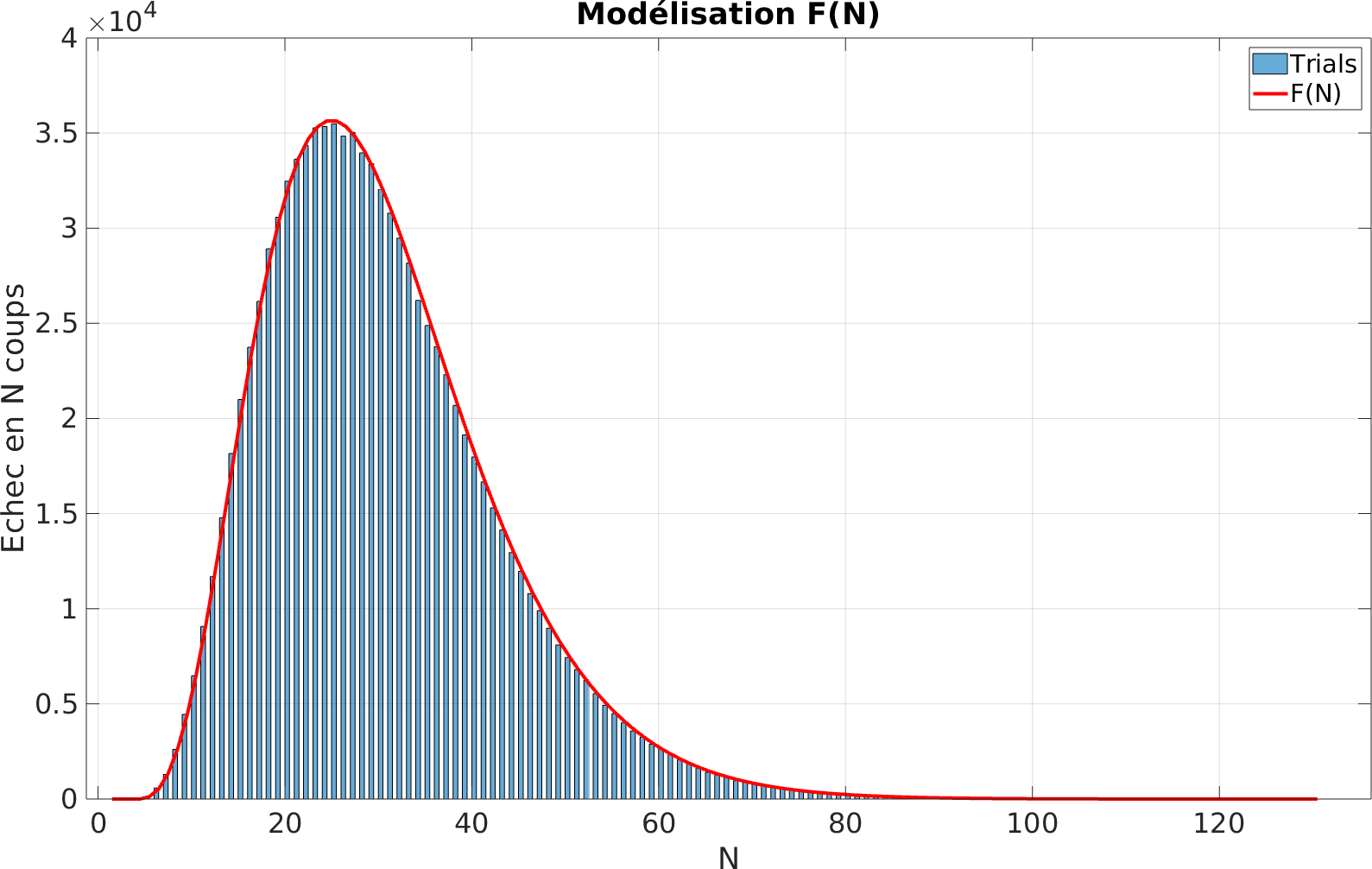
Sans cueillette des fruits, nous voyons que le Corbeau peut ainsi espérer gagner en moyenne en environ une trentaine de coups.

Il s’agit là pour lui d’une solution idyllique : il est quasi-certain (au sens des probabilités) de gagner en un nombre fini de coups. Dans les conditions de jeu réelles, les joueurs vont gagner cetaines parties ce qui va réduire drastiquement l’arbre des possibles pour notre pauvre corbeau. La figure ci-dessous illustre la modification de notre histogramme lorsqu’on introduit la possibilité de gagner pour les joueurs.

La surface d’histogramme manquante sur la figure de droite correspond exactement aux cas où les joueurs ont gagné.

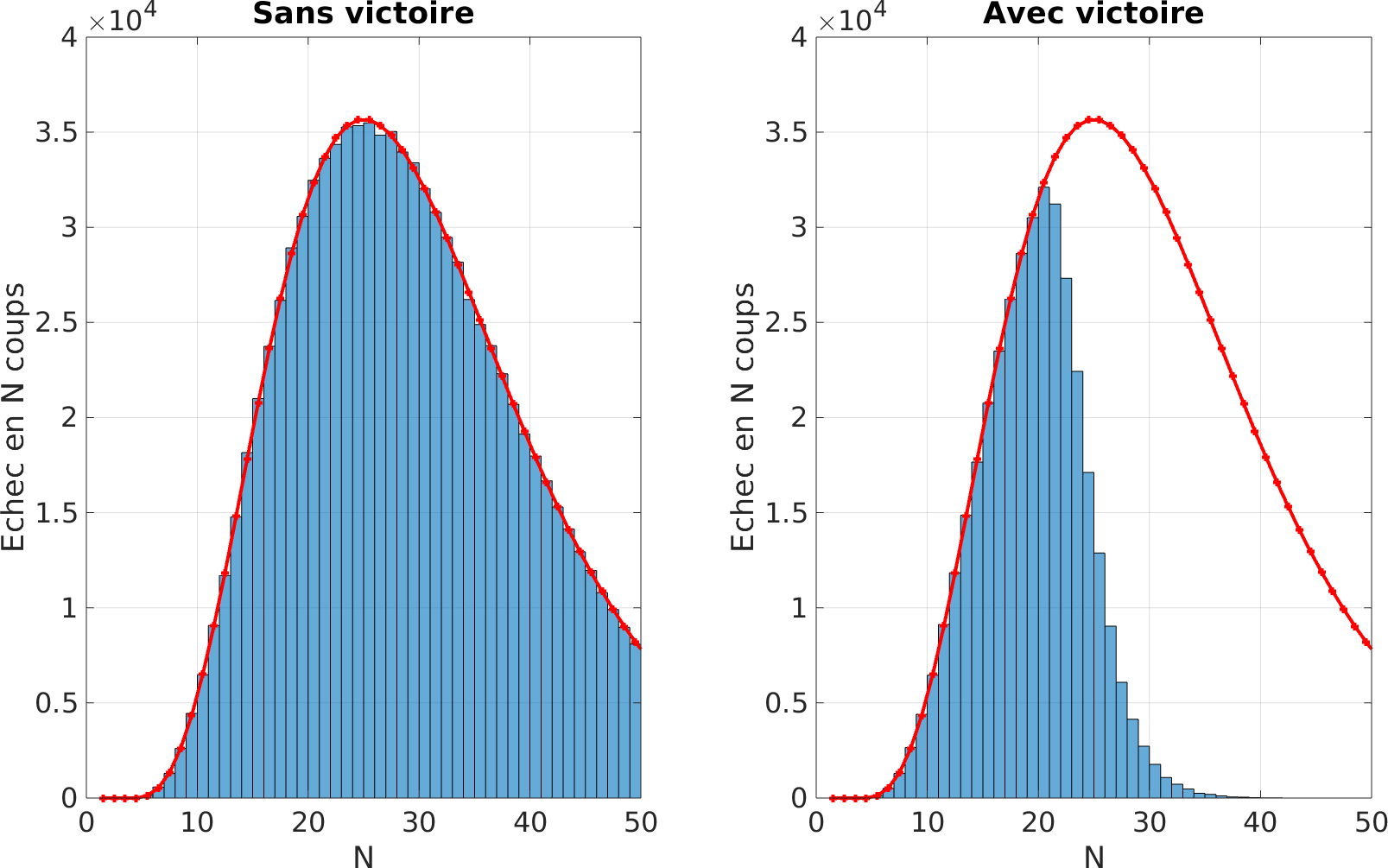
Il nous faut donc affiner notre modèle. Mais avant cela, nous allons étudier de la même façon la possibilité de victoire pour les joueurs.

Victoire en N coups

Ici nous faisons l’hypothèse inverse : le Corbeau ne peut jamais gagner.

Par soucis de simplification, je désactive également l’effet de la face Panier : lorsqu’on tombe dessus, il ne se passe rien de particulier (mais le tour est tout de même consommé). On peut assimiler cela à une face dont l’effet est simplement “Passez votre tour”.

Soit $W(N)$ la probabilité que les joueurs gagnent en exactement $N$ coups.

L’estimation de $W(N)$ est cette fois-ci un peu plus complexe dans le calcul des différents dénombrements. Je note les différents évenements R (Rouge), G (Vert), B (Bleu), Y (Jaune), P (Panier) et C (Corbeau). Comme on l’a dit, les faces P et C sont sans effet.

Déjà, une partie victorieuse en exactement $N$ coups se terminera nécessairement avec R, G, B ou Y. Supposons que ce soit R. Parmi les N-1 tirages précédents, on sait qu’il y a :

• Exactement 3 R
• Au moins 4 G
• Au moins 4 B
• Au moins 4 Y

J’introduis le nombre $S(n_r, n_g, n_b, n_y, N)$ qui représente le nombre de façons différentes d’avoir exactement $n_r$ faces R, $n_g$ faces G, $n_b$ faces B et $n_y$ faces Y parmi $N$ tirages successifs. On suppose bien entendu que $(n_r+n_g+n_b+n_y)<=N$. Un peu de combinatoire me donne directement :

\[S = {N \choose n_r}\cdot{N-n_r \choose n_g}\cdot{N-(n_r+n_g) \choose n_b}\cdot{N-(n_r+n_g+n_b) \choose n_y}\cdot2^{N-(n_r+n_g+n_b+n_y)}\]

Le nombre $\Omega_W (N)$ de façons différentes de gagner en exactement $N$ coups s’écrit alors :

\[\Omega_W (N) = 4\cdot \sum_{k_g=4}^{N-12} \quad \sum_{k_b=4}^{N-8-k_g} \quad \sum_{k_y=4}^{N-4-(k_g+k_b)} S(3, k_g, k_b, k_y, N-1)\]

Ce qui peut éventuellement se réécrire :

\[\Omega_W (N) = 4\cdot \sum_{k_g=0}^{N-16} \quad \sum_{k_b=0}^{N-12-k_g} \quad \sum_{k_y=0}^{N-8-(k_g+k_b)} S(3, 4+k_g, 4+k_b, 4+k_y, N-1)\]

La probabilité $W(N)$ s’écrit finalement :

\[W(N) = \frac{\Omega_W (N)}{\Omega} = \frac{\Omega_W (N)}{6^N}\]

La formule est un peu complexe (d’aucuns diraient imbitable) mais est en adéquation avec la simulation (comme nous allons le voir). J’aurais aimé obtenir quelque chose de plus simple. Le point délicat qui survient systématiquement concerne le calcul du nombre de permutations. Ainsi, dans le cas particulier d’une suite victorieuse d’exactement 16 coups, nous avons 4 possibilités de base, selon la couleur du 16ème et dernier lancé. Les 15 tirages précédents comportent exactement : 3 R, 4 B, 4G et 4 Y. Combien de suites de 15 tirages contiennent ces quantités exactes de couleurs ? Il faut passer par les permutations et ce nombre est :

\[\frac{15!}{(4!)^3\cdot3!}\]

La probabilité de victoire en 16 coups est alors :

\[W(16) = 4\cdot \frac{15!}{(4!)^3\cdot3!\cdot 6^{16}} \approx 2.24\cdot 10^{-5}\]

On obtient exactement le même résultat avec la formule de la triple somme (qui dans ce cas se limite à un simple terme où, nous n’avons pas le choix, $k_g=k_b=k_y=4$).

Mais si nous considérons maintenant le calcul de $W(17)$, et en supposant (pour simplifier) que le 17eme lancé soit un R, alors nous devons envisager pour les nombres $[n_r, n_g, n_b, n_y]$ des 16 premiers lancés les cas suivants :

• $[3, 4, 4, 4]$ : nous avons obtenu exactement un dé neutre (P ou C)
• $[3, 5, 4, 4]$ : nous aurons tiré un G de trop et aucun dé neutre
• $[3, 4, 5, 4]$ : nous aurons tiré un B de trop et aucun dé neutre
• $[3, 4, 4, 5]$ : nous aurons tiré un Y de trop et aucun dé neutre

Pour chacun de ces 4 cas, le dénombrement des permutations possibles sera sensiblement différent, d’où la tronche de l’équation de $W(N)$. Peut-être qu’il y a une astuce (par exemple, compter plutôt le complémentaire, à savoir aucune victoire en exactement $N$ coups; ou encore compter dénombrer différemment). Il est également possible que la formule se simplifie, en se rappelant que :

\[{n \choose k} = \frac{n!}{k!\cdot(c-k)!}\]

En y regardant de plus près, il est possible que les termes de la sommation se regroupent en utilisant la formule de Pascal :

\[{n \choose k} +{n \choose k+1} = {n+1 \choose k+1}\]

par exemple, voici à quoi ressemble, sans simplification, la distribution des coefficients $n \choose k$ qui interviennent dans le calcul de $W(N)$ pour différentes valeurs de $N$ (entre 16 et 30).

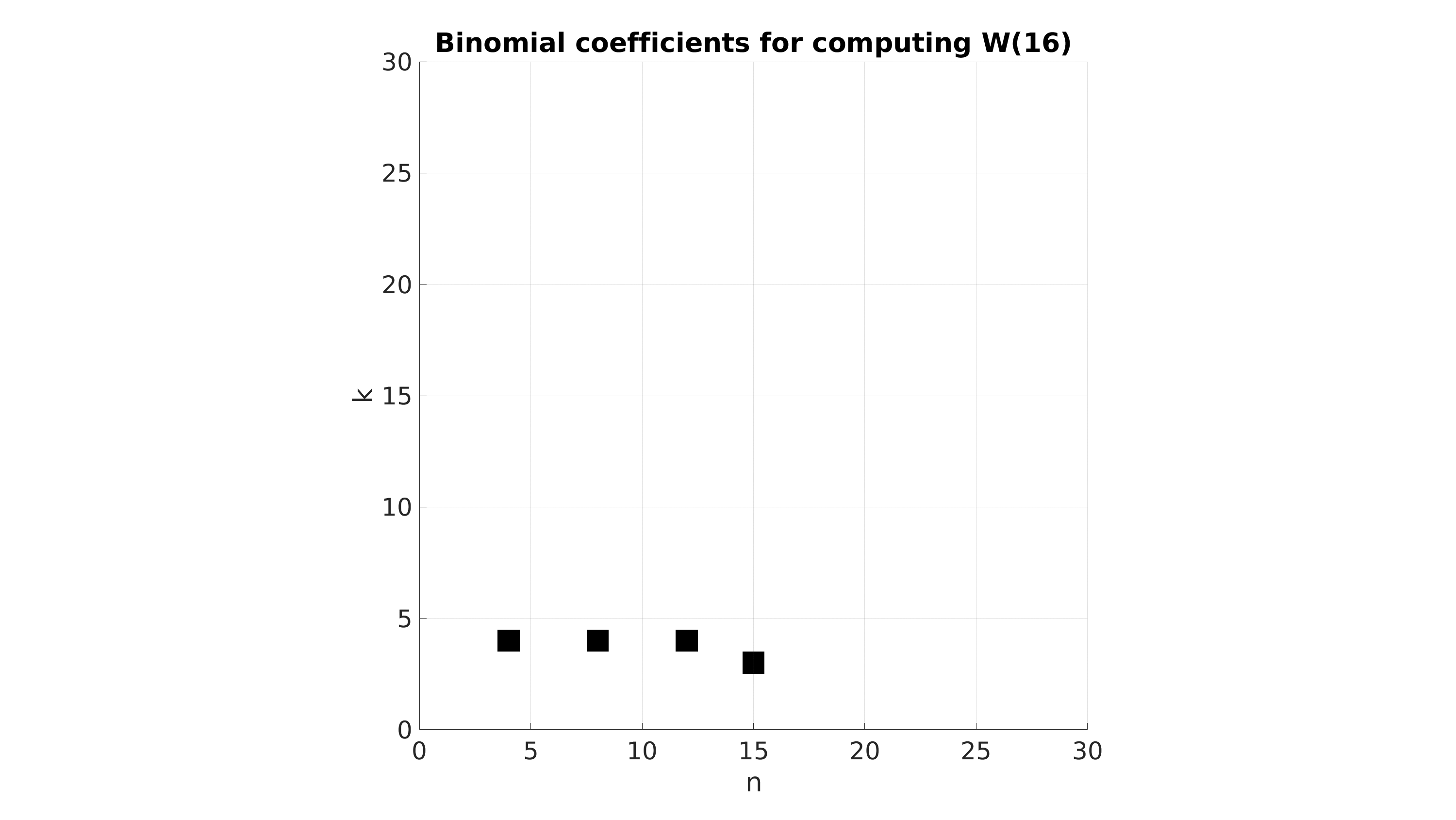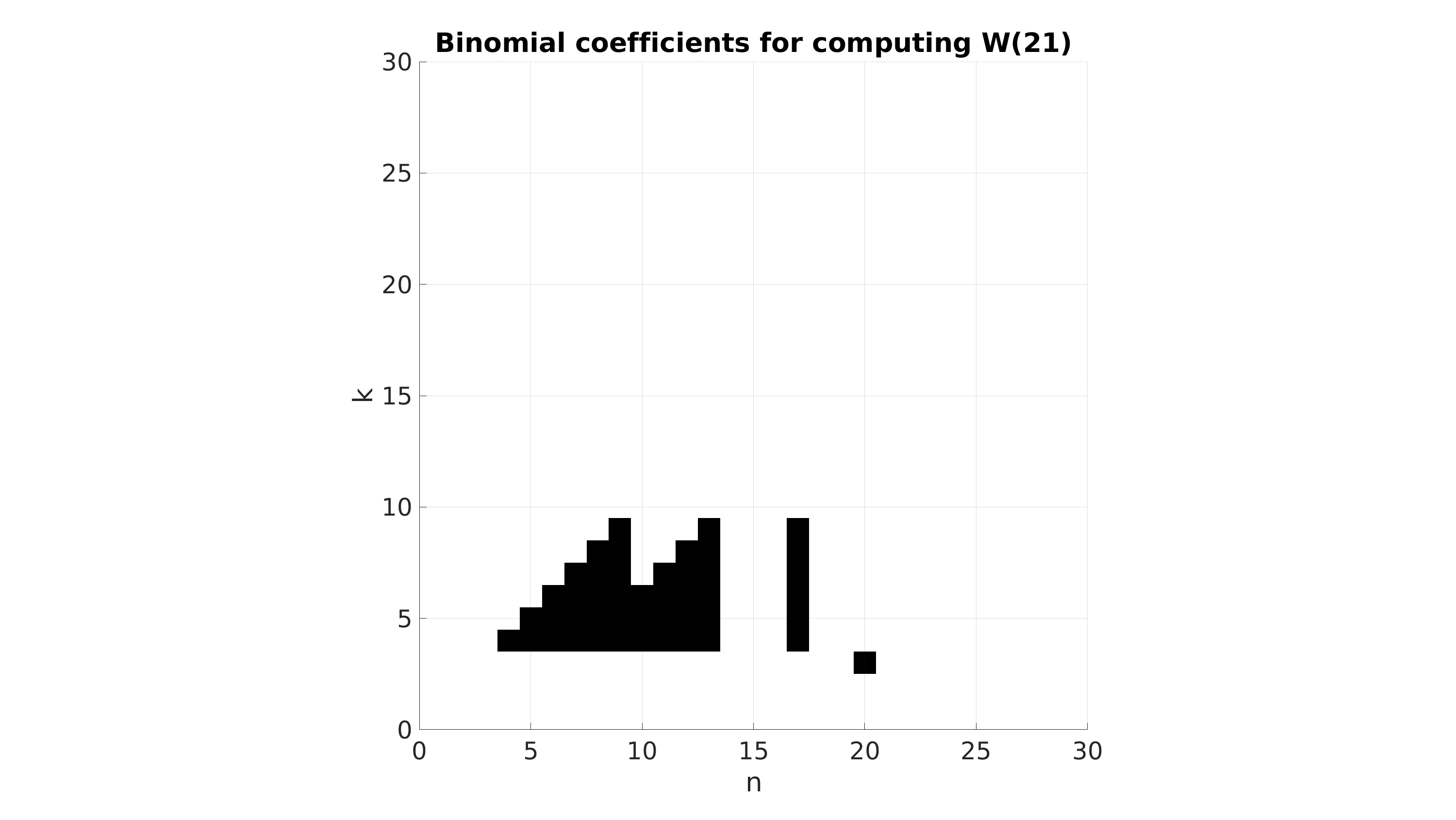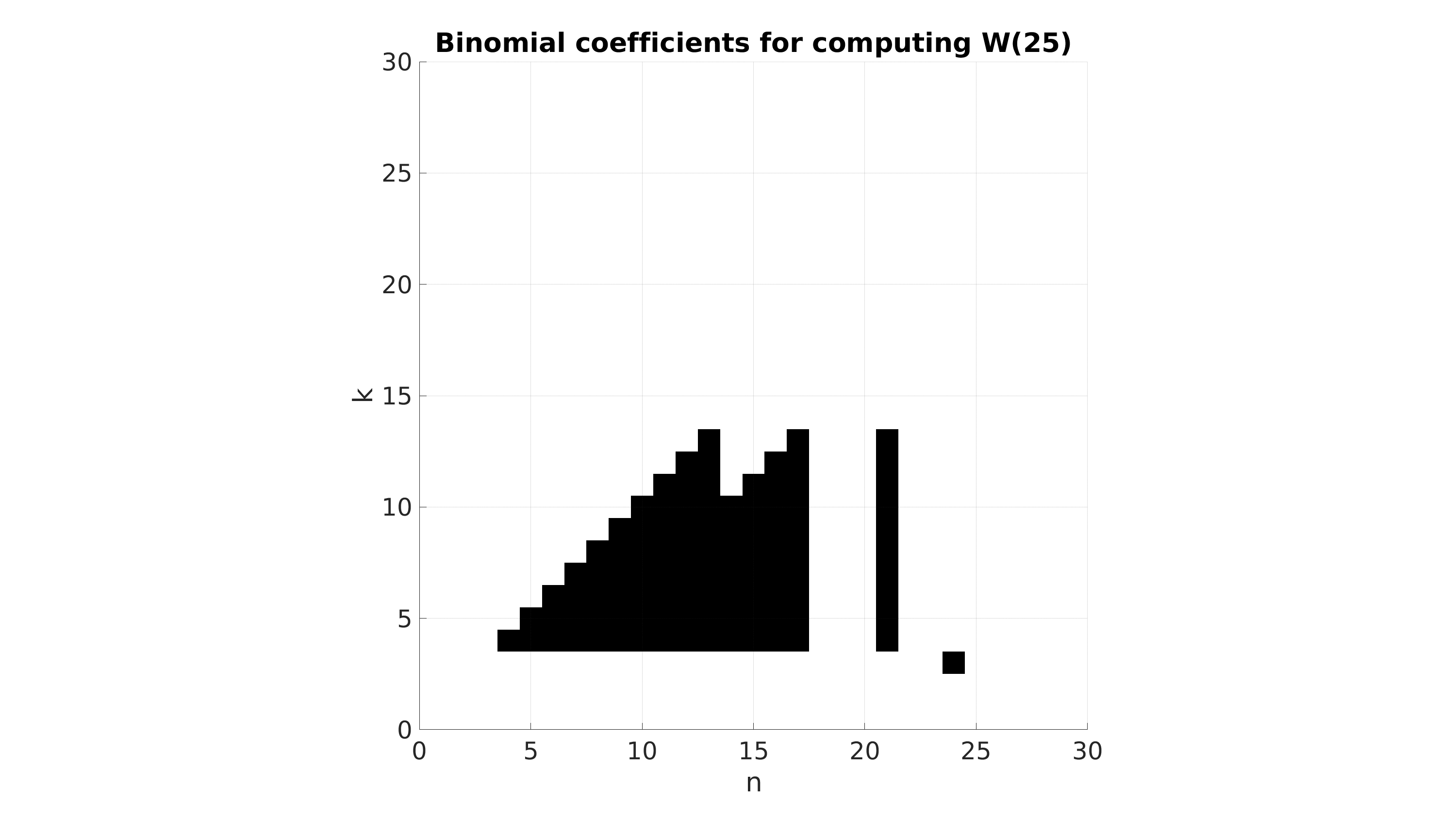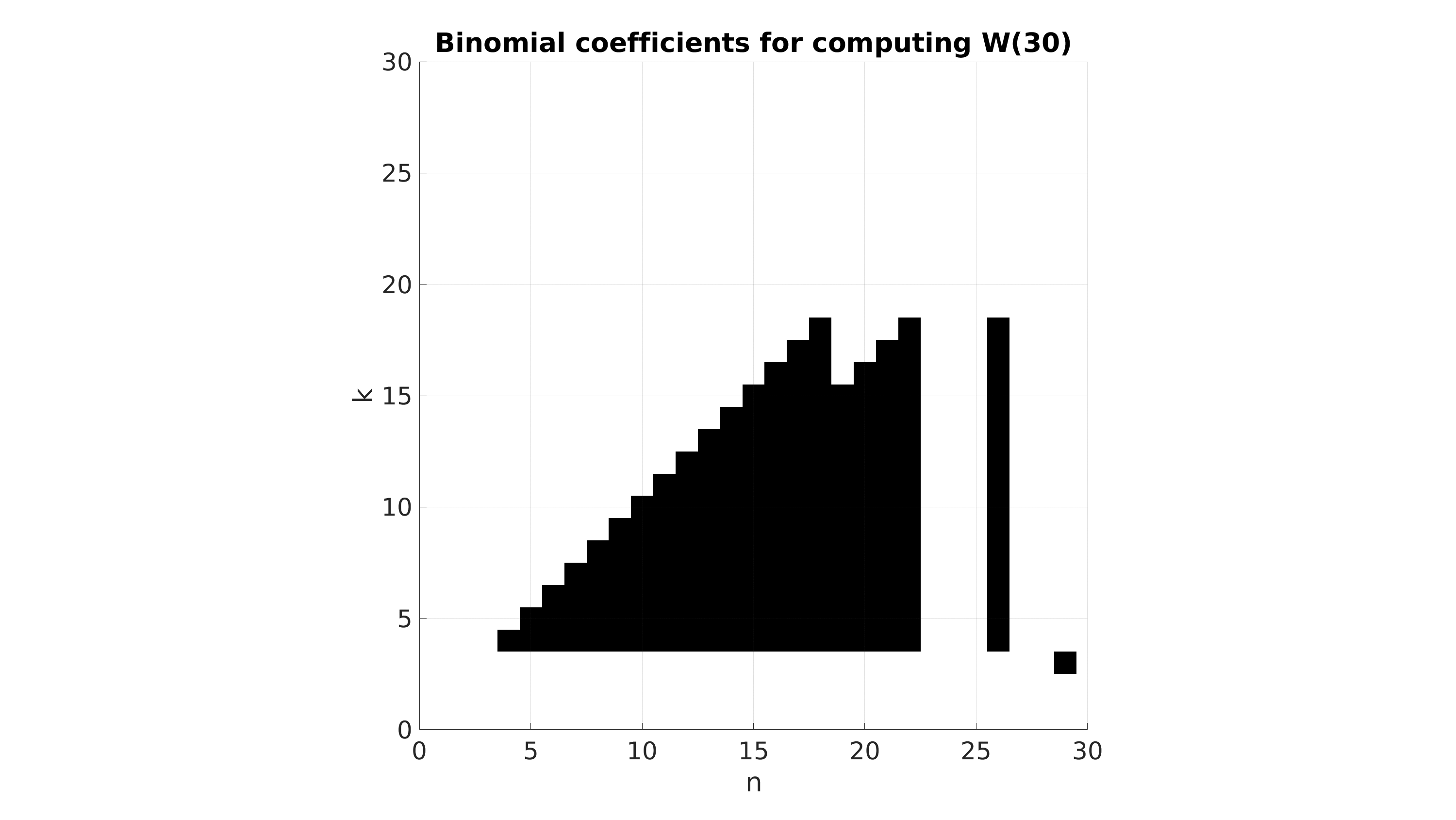
Mais enfin, laissons cela de côté et restons sur cette expression de $W(N)$. Ce nombre représente, je le rappelle car il est facile de s’y perdre lorsqu’on manipule tous ces coefficients, la probabilité de gagner le jeu en exactement $N$ lancés de dé dans l’hypothèse simplificatrice où le corbeau ne peut pas gagner et où la face Panier ne fait rien.

Si nous comparons notre expression de $W(N)$ avec une simulation de Monte-Carlo de 1 million de parties jouées selon les règles de cette mécanique simplifiée, alors nous obtenons une excellente adéquation (comme pour le cas de $F(N)$) :

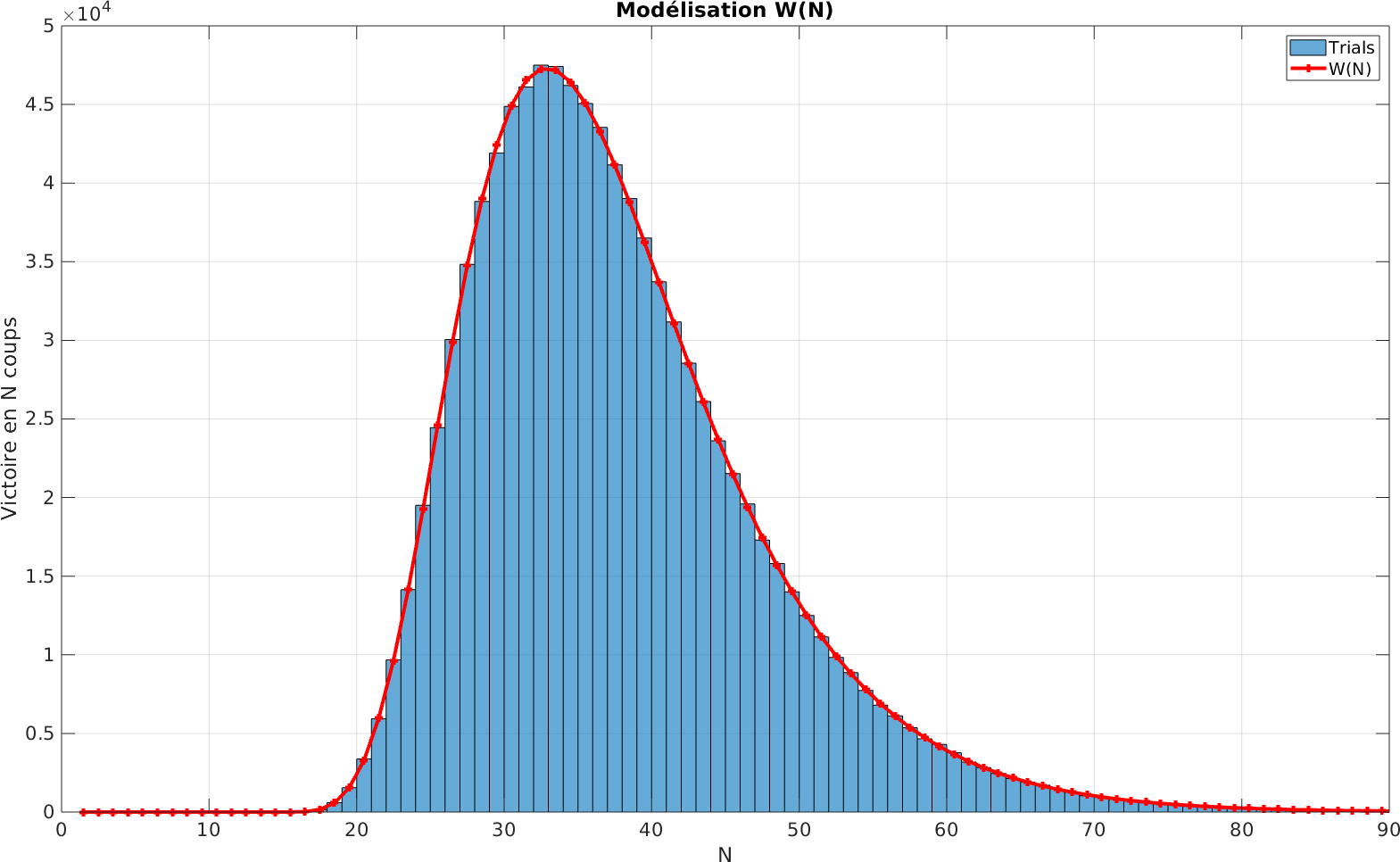
SI nous rajoutons la possibilité au Corbeau de gagner, nous observons de même que précedemment, un dépeuplement des états gagnants à haute valeur de $N$, comme on l’observe ci-dessous. C’est un comportement prévisible : faire durer une partie gagnante c’est augmenter la probabilité du Corbeau de gagner. Et de la même façon, si le Corbeau prend trop son temps pour gagner, il laisse la main aux joueurs pour cueillir tous les fruits !

Plus amusant, si on ajoute la mécanique de la face Panier, alors la distribution se resserre drastiquement ! La encore c’est prévisible : utiliser le Panier, c’est augmenter les chances de succès et donc diminuer les probabilités de succès associées aux longues parties.

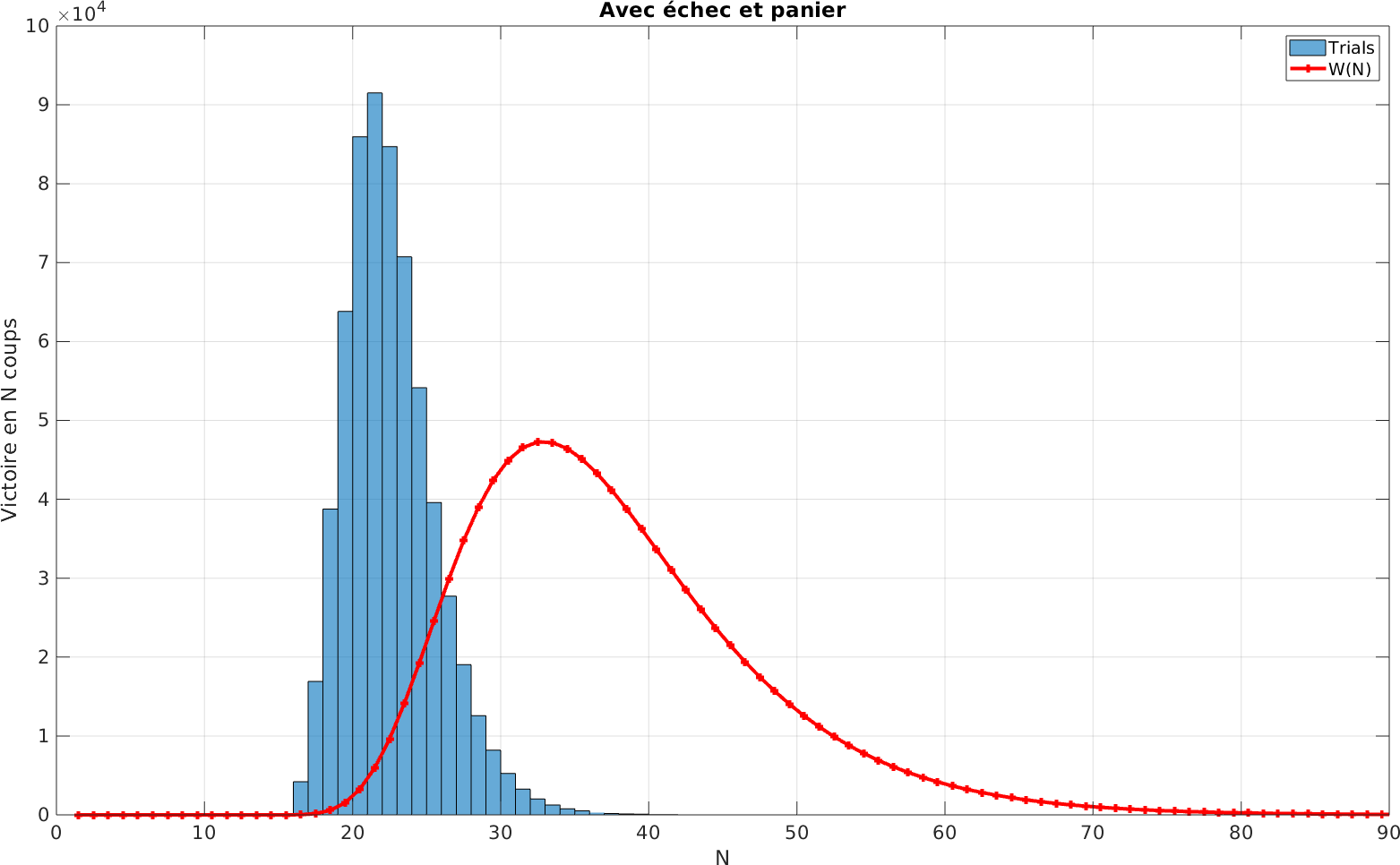
Ces informations sont résumées dans le tableau ci-dessous (statistiques estimées sur un million de parties à chaque fois).

Dé Corbeau	Dé Panier	Nombre de coups moyen pour gagner
Désactivé	Désactivé	37
Activé	Désactivé	30
Activé	Activé	22

Cas général

Pour calculer les probabilités de gain ou de défaite en $N$ coups avec toutes les règles du jeu actives en même temps, il nous faut raisonner différement.

Par exemple, perdre une partie à l’étape $k$ avec $k < N$, c’est restreindre l’univers $\Omega$ des configurations possibles à envisager pour les parties de $N$ coups. Ainsi nous ne devrions plus normaliser par $6^N$ mais par un nombre plus petit. Pour le dire autrement, le fait qu’on gagne en $N$ coups présuppose que nous n’avons ni gagné ni perdu pendant les $N-1$ coups précédents.

La solution pour s’en sortir est, je pense, de faire appel aux probabilités conditionnelles. On aboutirait peut-être à quelque chose qui ressemble à ça :

\[W(n) = \frac{\Omega_W (N)}{\Omega}\] \[F(n) = \frac{\Omega_F (N)}{\Omega}\]

Avec :

\[\Omega = 6^N-\sum_{k=1}^{N-1} (\Omega_W(k) + \Omega_F(k))\cdot 6^{N-k}\]

Mais je ne suis pas trop sûr de ce truc là². Et par ailleurs, le fait de ne pas avoir d’expression simple de $W(N)$ est assez décourageant à ce stade. Peut-être aussi qu’il n’existe pas de formule simple pour capturer la dynamique de ce jeu.

Par ailleurs, une autre approche possible serait de modéliser le nombre de fruits restant sur un arbre par un automate fini probabiliste. On aurait un truc comme ça :

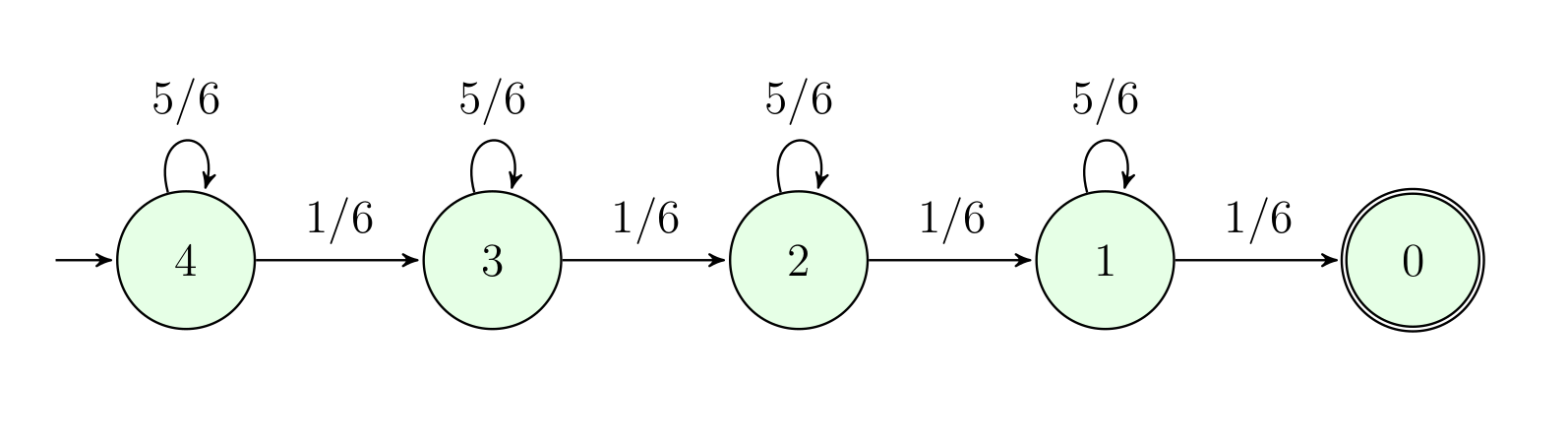
La matrice de transition pourrait s’écrire :

\[M = \begin{pmatrix} 5/6 & 0 & 0 & 0 & 0 \\ 1/6 & 5/6 & 0 & 0 & 0 \\ 0 & 1/6 & 5/6 & 0 & 0 \\ 0 & 0 & 1/6 & 5/6 & 0 \\ 0 & 0 & 0 & 1/6 & 1 \\ \end{pmatrix}\]

Et donc pour connaître la probabilité d’état au bout de $k$ lancés, il suffit de regarder le vecteur $M^k\cdot u_4$ avec $u_4 = (1\, 0\, 0\, 0\, 0)’$ qui représente l’état initial. On obtient alors ce genre de graphiques qui représente l’évolution en fonction du nombre de lancés de dé de la probabilité qu’il reste $n$ fruits sur un arbre donné (avec $0 \leq n \leq 4)$ :

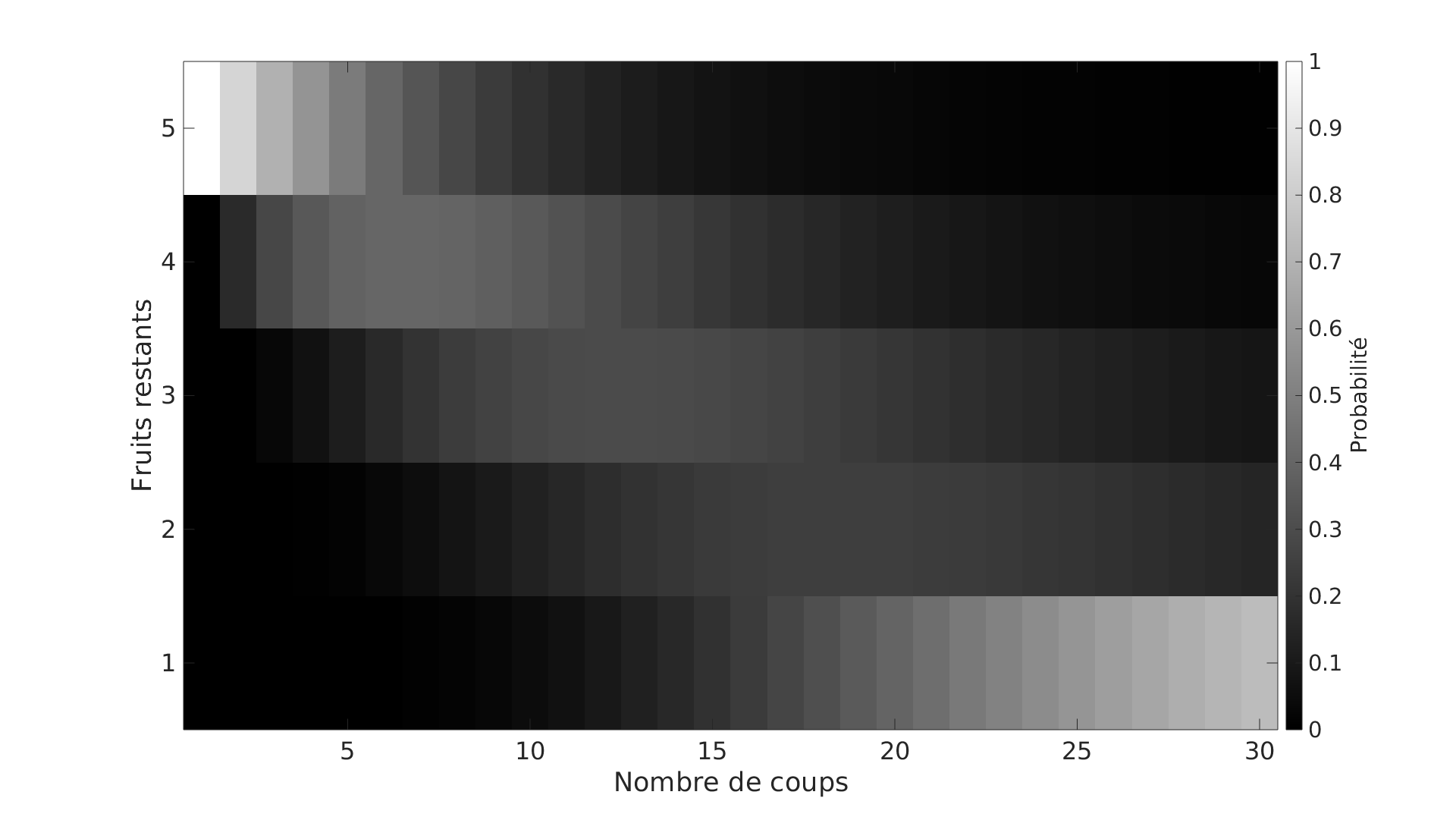
Mais bon, je vais en rester là.

Simulation de Monte-Carlo

Il est en revanche beaucoup plus facile d’estimer les chances de succès et d’échecs en laissant l’ordinateur jouer un très grand nombre de parties différentes (un million). C’est ce que je présente ici.

Pour le modèle de jeu, la seule incertitude (si j’ose dire) concerne la face Panier qui laisse le joueur décider de l’arbre sur lesquel prélever un fruit. Paradoxalement, c’est quand notre action est certaine que cela rend mon programme plus incertain.

J’ai opté pour la stratégie suivante : si la face Panier sort, alors on prélève un fruit sur l’arbre qui en contient le plus. C’est la stratégie la plus efficace. Mais si plusieurs arbres possèdent exactement ce nombre maximal, alors je prélève selon un ordre arbitraire (toujours le même).

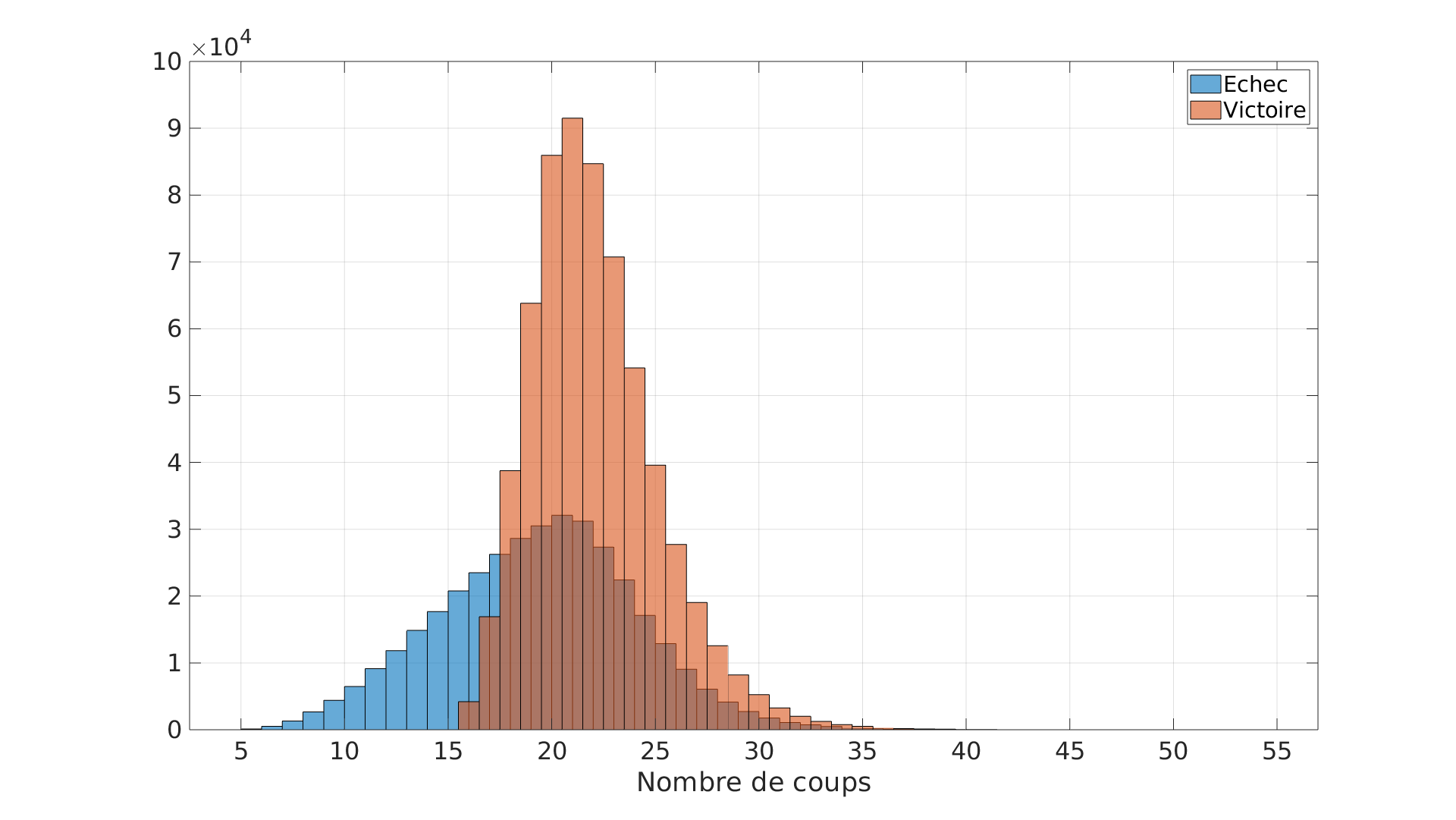
Au final, comme nous l’avons dit au début, ce qui ressort de ces simulations c’est que les joueurs gagnent dans 63% des parties environ.

Le Corbeau gagne en moyenne en 18 coups alors que les joueurs gagnent en moyenne en 22 coups, ce qui fait qu’une partie se déroule en moyenne en 20 coups. A raison de 30 secondes par tour, une partie moyenne dure 10 minutes ce qui est conforme aux indications fournies sur la boîte de jeu. Ces trente secondes peuvent paraître excessive mais n’oublions pas d’une part que ce jeu est à partir de 2 ans et que d’autre part on papote et on rigole pendant qu’on joue !

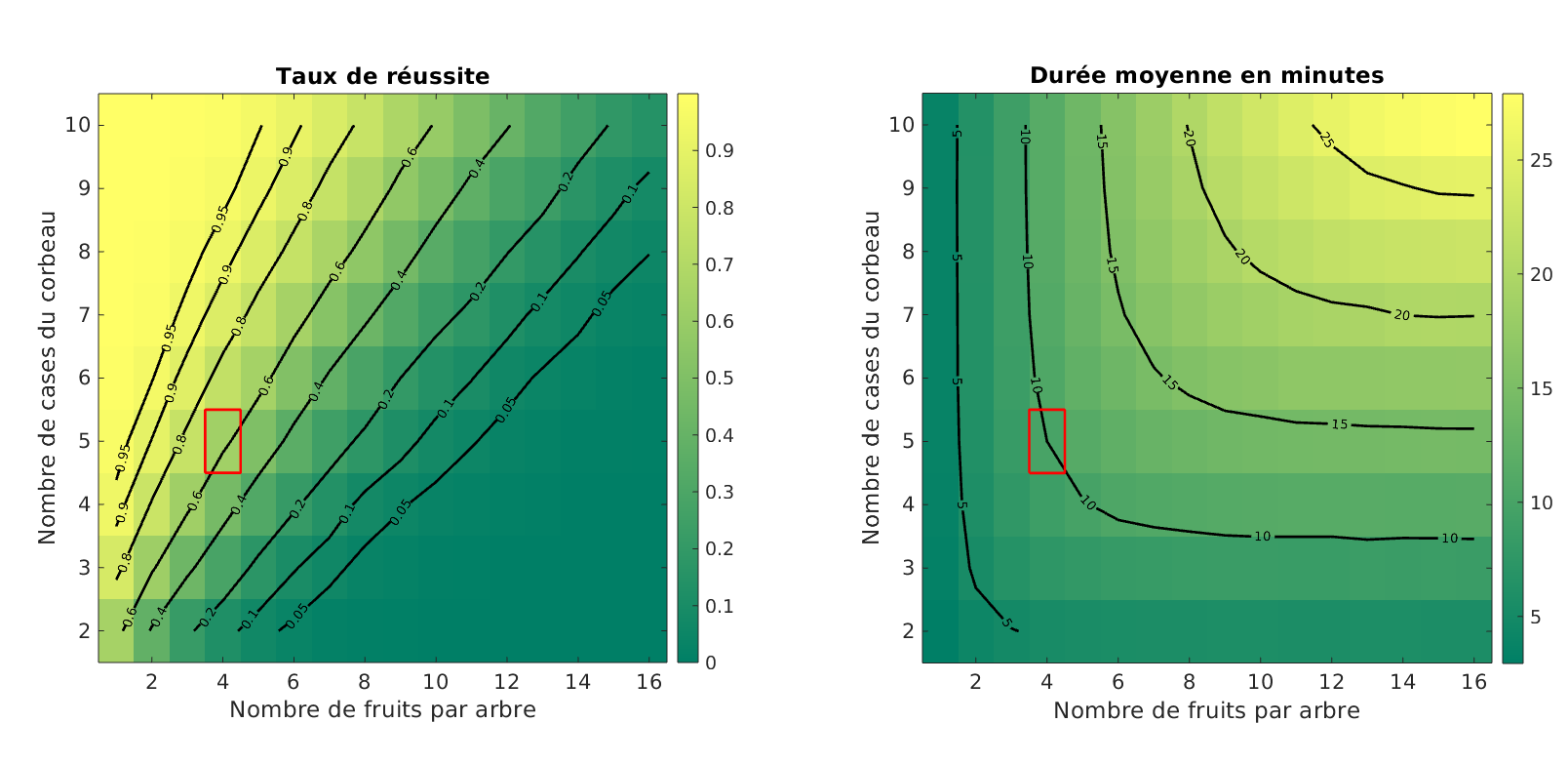
Plus amusant, on peut aussi modifier légéremment les règles du jeu et voir en quoi cela affecte les chances de succès.

Les paramètres d’entrées que nous faisons varier :

• le nombre de cases du Corbeau (plus ce nombre est élevé, plus grandes sont nos chances de succès)
• le nombre de fruits par arbre (plus ce nombre est élevé, plus faibles sont nos chances de succès)

Les paramètres de contrôle :

• probabilité empirique de succès
• durée moyenne d’une partie (en minute)

1. SMULLYAN, Raymond M. Satan, Cantor and infinity (and other mind-boggling puzzles). New York : Knopf, 1992. Plus d’informations sur la page de l’éditeur ↩

2. je me relis et je me rends compte que c’est faux. Dans les parties gagnantes en $N$ coups, il y en a nécessairement certaines qui ont échoués au bout de $k < N$ coups lorsque $N$ est suffisament grand. Pas le choix, il faut vraiment passer par les probabilités conditionnelles. ↩