Un loups-garous maison

Pour son prochain goûter d’anniversaire, ma fille Marie de six ans conviera quelques amis à elle. Je me suis demandé s’ils étaient en âge d’apprécier une petite partie de loups-garous simplifiée (et édulcorée).

Pour estimer cela, j’ai créé avec Marie un jeu de cartes simplifié et j’ai mis à contribution la famille proche pour une partie pilote.

Nous étions en tout six personnes : Marie, ses grands-parents (Pépé et Mémé), ma soeur et son mari (Tata et Tonton) et moi-même. Durant l’expérience nous étions donc trois joueurs aguerris (Tata, Tonton et Papa), deux joueurs débutant (Pépé et Mémé) et une enfant de six ans dont je scrutais les réactions et les stratégies lors de la partie. Notons que le cousin nous a rejoint en milieu de séjour et nous avons pu tester également quelques variations.

Je n’envisageais pas spécialement de billet de blog autour de cette histoire sauf que je me suis heurté rapidement à une petite difficulté : les Loups-Garous de Thiercelieux, tels qu’ils ont été conçus par leurs créateurs Philippe des Pallières et Hervé Marly, ne sont prévus que pour 8 à 18 joueurs.

Etant donné qu’il faut au moins un loup-garou pour que la partie ait un sens et qu’il y a exactement un loup-garou dans la partie minimale à 8 joueurs, le problème fut vite réglé : à six joueurs, nous devons avoir également 1 loup-garou. Néanmoins, je me suis dit que la partie sera plus facile pour ce loup-garou étant donné qu’il y a 2 villageois en moins.

Plus facile mais de combien exactement ?

Les nombres de villageois et de loups-garous étant par définition entiers, le ratio de loups-garous dans le village ne peut prendre que certaines valeurs rationnelles. Partant de là, la difficulté de la partie pour un loup-garou, doit sensiblement varier selon le nombre de participant.

Le présent billet de blog a la prétention d’étudier un peu tout cela par l’intermédiaire d’un modèle simplifié.

• Les règles du loup-garou simplifié
• Modèle du jeu
• Loi discrète uniforme
• Simulation du jeu selon les répartitions $(v, l)$ canoniques
• Simulation du jeu avec une répartition $(v, l)$ quelconque
• Améliorations du modèle
• Le cas particulier à 6 joueurs
• Le jeu de loups-garous maison

Les règles du loup-garou simplifié

Nous avons une ensemblée de $N$ habitant d’un village. Ces habitants comportent $N_l$ loups-garous, qui se transforment en loup la nuit, et $N_v$ villageois normaux. Nous avons donc :

\[N = N_v + N_l\]

Je fais ici la distinction entre habitant (qui peut être loup-garou ou non) et villageois (qui n’est par définition pas un loup-garou).

Un tour de jeu se déroule en deux phases : la nuit et le jour.

Pendant la nuit, les loups-garous se réveillent et éliminent un villageois de leur choix.

Pendant la journée, les habitants (qui incluent donc les loups-garous) discutent entre eux pour éliminer l’un des leurs. Avec un peu de chance, ils élimineront un loup-garou.

La partie s’arrête lorsqu’il n’y a plus de loup-garou auquel cas les villageois restant gagnent la partie; ou bien lorsqu’il n’y a plus de villageois auquel cas les loups-garous restant gagnent.

Remarquons déjà que les villageois ne peuvent gagner la partie que lors d’une phase de jour lorsqu’ils éliminent le dernier loup.

Les loups-garous de leur côté peuvent gagner de nuit comme de jour : de nuit, comme conséquence d’une de leur attaque; et de jour comme défaillance des villageois à éliminer un loup.

Dans le jeu de base se trouvent quelques autres personnages (Cupidon, le Voleur, la Voyante, la Sorcière, le Chasseur…) mais j’ai décidé de les ignorer afin de garder la mécanique la plus simple possible. Je garde toutefois à l’esprit que l’ensemble de ces personnages (à l’exception de Cupidon et du Voleur) ont tendance à favoriser les villageois (ainsi la Voyante est une villageoise qui peut une fois par nuit découvrir la véritable nature d’un habitant de son choix). Globalement ces cartes augmentent sensiblement le pouvoir des villageois (pensons à la Sorcière, une villageoise qui une fois dans la partie peut tuer la personne de son choix) : bien utilisé, ce pouvoir est profitable aux villageois mais il peut aussi se retourner contre eux.

Modèle du jeu

Un tour de jeu se déroule donc en deux phases successives : la nuit, puis le jour.

Nous pouvons représenter l’état du jeu en un instant $t$ comme un point sur le quart de plan $(v, l)$.

Voici un exemple dans le cas général, le point en rouge correspond à l’état courant :

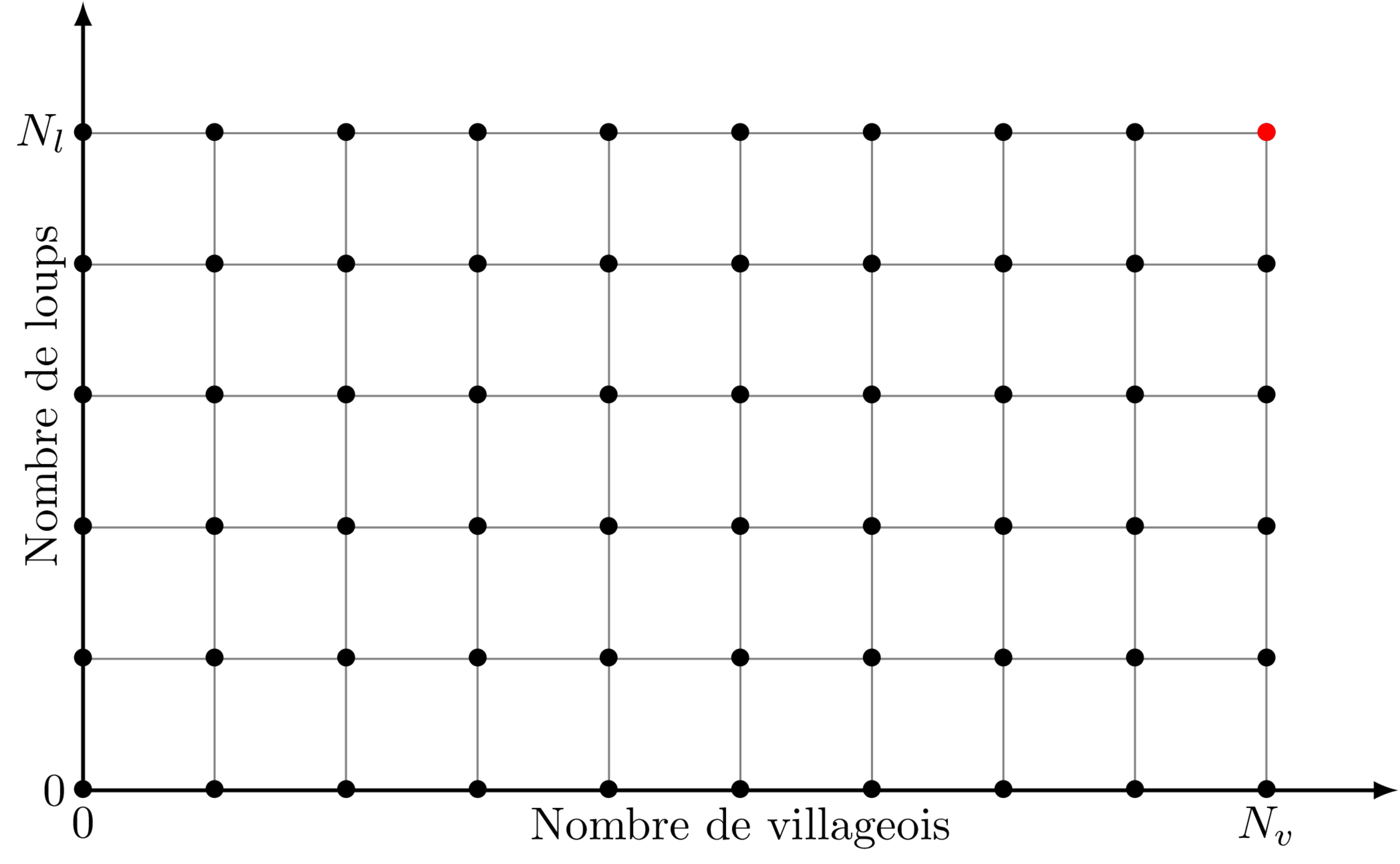
Les règles du jeu font que nous ne pouvons créer ni de villageois ($v$ augmente) ni de loups-garous ($l$ augmente).

Afin de simplifier les schémas, nous considérons (sans perte de généralité) le cas particulier où $N_v=5$ et $N_l=2$

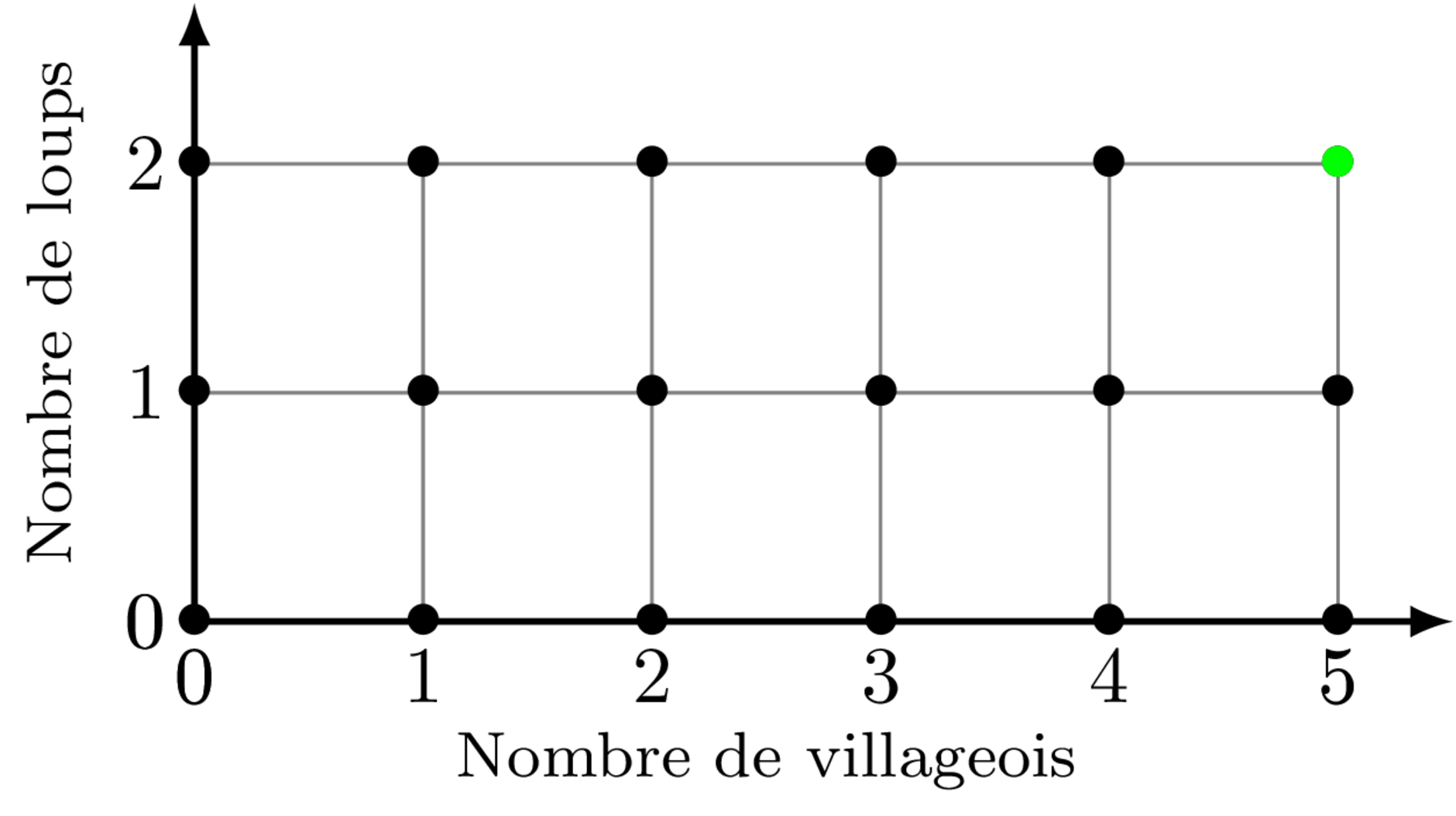
Lors d’une phase nuit et selon nos règles simplifiées, un villageois est nécessairement tué. Cet opérateur descend donc le compteur $v$ d’une unité avec une probabilité de $1$.

Lors d’une phase jour, ce sera soit un villageois soit un loup-garou qui sera tué. Si nous notons $p$ la probabilité qu’un loup soit tué, alors nous pouvons représenter un tour de jeu selon le diagramme suivant :

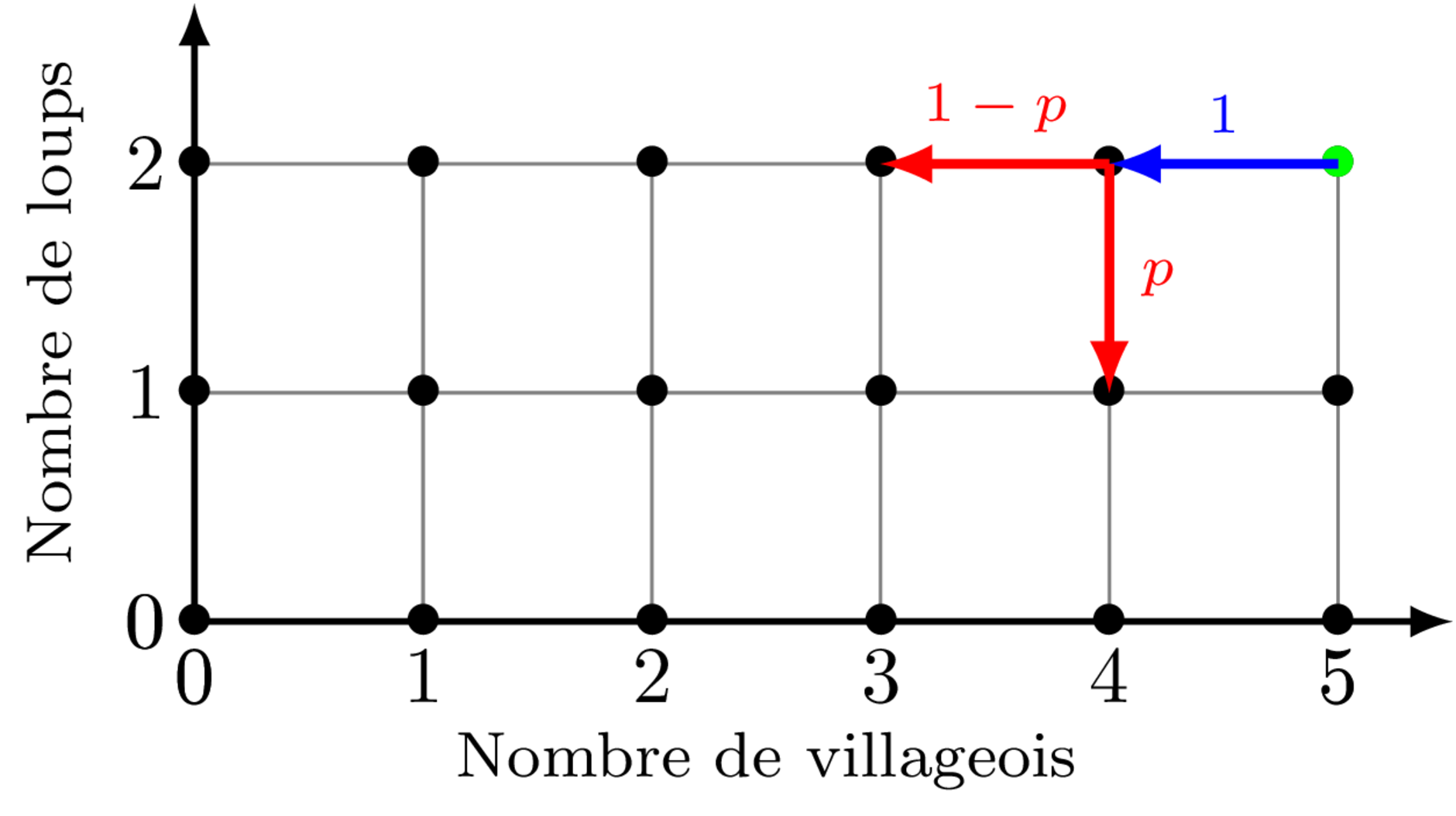
La partie s’arrête lorsque le point courant touche l’axe des abscisses, auquel cas $l=0$ et les villageois gagnent; ou bien lorsque ce point touche l’axe des ordonnées et dans ce cas $v=0$ et les loups-garous gagnent. Selon notre modèle, le point de coordonnées $(0,0)$ où il ne reste plus ni loups-garous ni villageois est indéterminé (qui est le vainqueur dans un village vide ?). Mais cela n’est pas important car ce point est inacessible sans passer au préalable par une condition de victoire.

Tout l’interêt du modèle est ici de choisir une valeur de $p$ réaliste. Alors bien sûr cela va dépendre de plusieurs facteurs qui peuvent difficilement être intégrés dans mon modèle :

• les loups-garous peuvent être maladroit, faire du bruit, bousculer les voisins en désignant leur victime etc.
• mais de la même façon, un villageois agité pendant la phase nuit pourra être accusé à tort d’être un loup
• les joueurs peuvent être plus ou moins persuasifs dans leur argumentation, plus ou moins manipulateurs dans leur stratégie
• les inimitiés ou les amitiés fortes peuvent influencer peut-être le vote

J’élimine rapidement le cas trop simplifié qui consisterait à prendre $p$ constant, par exemple $1/2$. Dans ce cas, lors de la phase jour, les habitants auraient une chance sur deux d’éliminer un loup-garou et une chanche sur deux de tuer un innocent villageois. La simplicité de ce modèle est attirante mais nous n’aboutirions pas à une situation réaliste : imaginez par exemple 100 habitants parmis lesquels se cache un unique loup-garou. Il faudrait avoir une sacré chance pour l’éliminer lors d’une phase jour.

Loi discrète uniforme

Une loi plus réaliste serait de choisir uniformément parmi les $v+l$ survivants la personne à éliminer. Nous utilisons donc une loi de probabilité discrète uniforme et chaque personne à la même probabilité $1/(v+l)$ d’être éliminé. Nous avons donc :

\[p = \frac{l}{v+l}\]

et donc logiquement :

\[1-p = \frac{v}{v+l}\]

Rappelons que $p$ représente la probabilité que les habitants désignent un loup-garou lors du vote. Le fait d’utiliser une loi uniforme traduit le fait que ces derniers n’ont aucun a priori sur l’identité des loups. C’est justifiable pour les villageois, qui n’auraient ainsi jamais aucune information sur les loups. Ca l’est quand même moins pour les loups qui, eux aussi, votent un peu au hasard. Notre modèle montrera donc ses limites dans le cas où le nombre de loups n’est plus négligeable devant le nombre de villageois. Mais enfin qu’importe c’est une premier essai.

Simulation du jeu selon les répartitions $(v, l)$ canoniques

Avec cette mécanique, nous pouvons modéliser le comportement des joueurs de loups pour les couples $(N_v, N_l)$ prévus dans les règles :

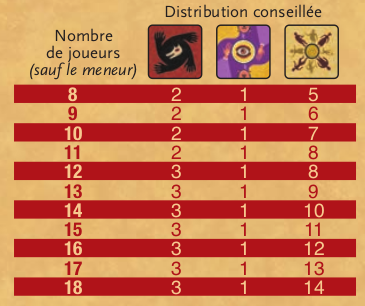
Rappelons que dans notre modèle simplifié, la voyante est une villageoise comme les autres.

Nous avons simulé 10 000 parties pour chaque couple $(N_v, N_l)$ prévus dans le livret. Nous en extrayons ensuite la fréquence de victoire des loups pour chaque cas. Nous obtenons alors le diagramme suivant :

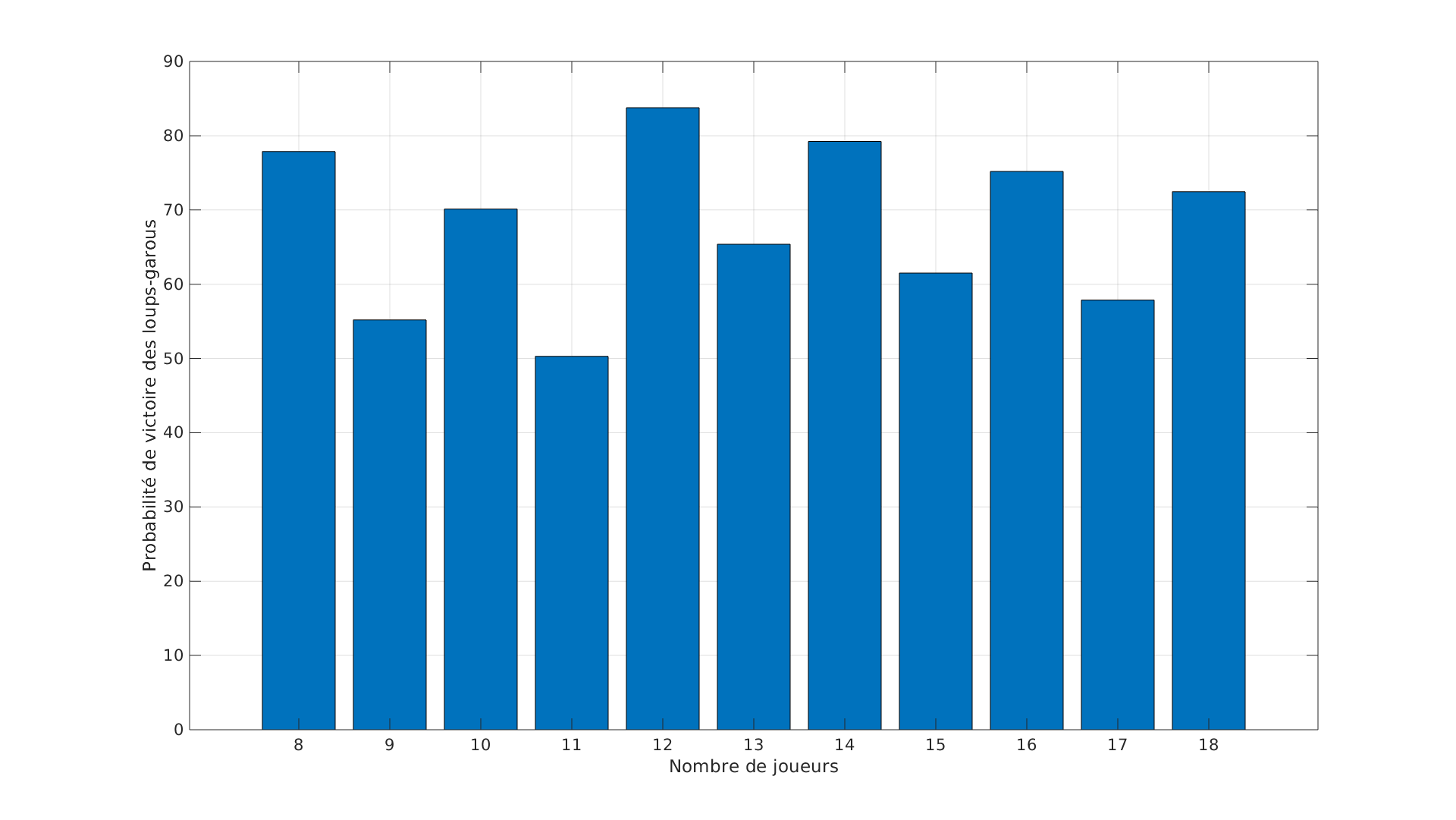
Nous observons plusieurs faits remarquables :

1. globalement les loups sont super avantagés par le jeu ! Ils gagnent en moyenne dans 68% des cas. On peut penser que les personnages additionnels (le Chasseur, la Sorcière, la Voyante) peuvent potentiellement leur compliquer la tâche… à condition que leur pouvoir soit utilisé à bon escient
2. la gigue qu’on observe n’est pas due à un faible échantillon mais est caractéristique du modèle : les loups ont toujours un avantage supplémentaire avec un nombre initial pair de joueurs. Ceci peut sembler étrange mais s’explique facilement par la dissymétrie jour/nuit. Je serai intéressé de savoir si des gros gros joueurs du jeu ont noté cet effet…
3. on voit très nettement l’effet de l’introduction du 3eme loup-garou à partir de 12 joueurs

Je reste malgré tout perplexe devant les forts taux de victoire des loups… Ce n’est pas le sentiment que j’avais en jouant au jeu. Et n’oublions pas que nous modélisons des loups idiots qui peuvent potentiellement voter contre leurs congénères.

Peut-être ai-je minimisé notre capacité à débusquer la duperie.

Simulation du jeu avec une répartition $(v, l)$ quelconque

Voici cette même fréquence de victoire des loups lorsqu’on fait varier, d’une part le nombre de villageois entre 1 et 20 et d’autre part le nombre de loups entre 1 et 5.

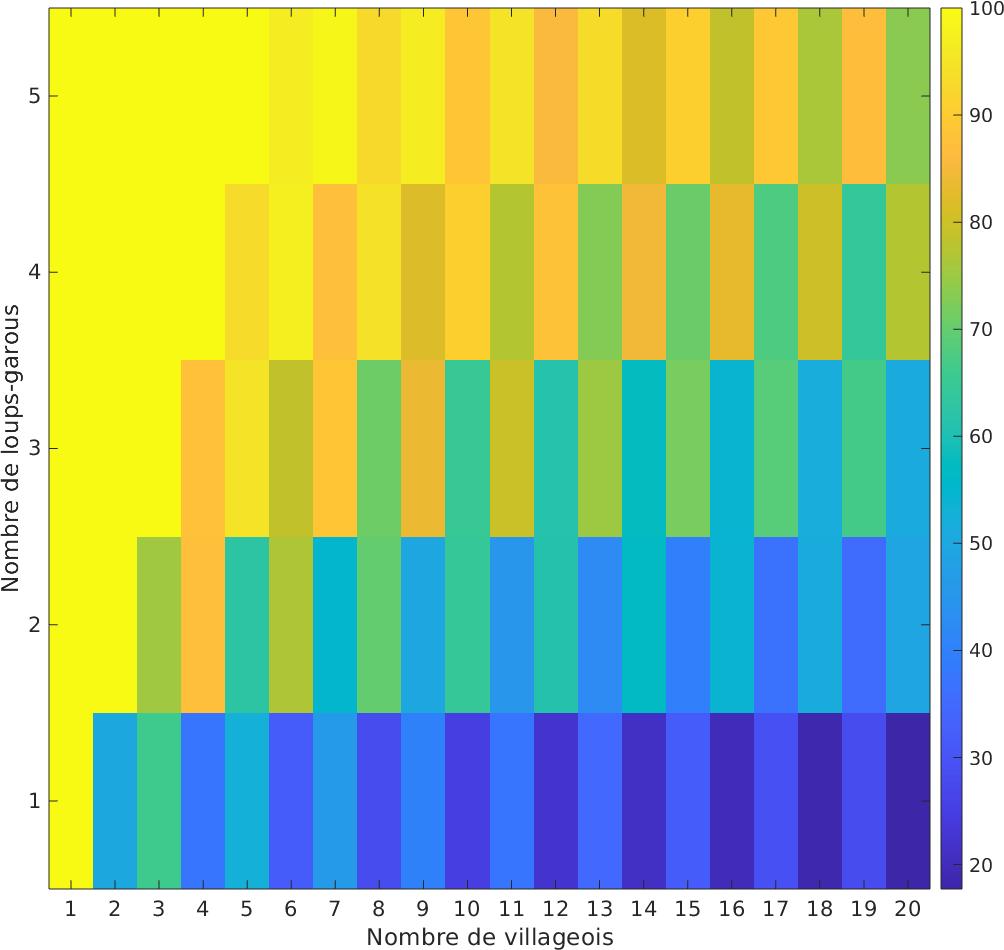
Sans surprise on constate que ce taux augmente avec le ratio $l/v$. Nous retrouvons également la dissymétrie jour/nuit qui confère un avantage aux loups lorsque le nombre de joueur est pair.

Améliorations du modèle

Peut être faudrait-il modéliser plus finement les mécaniques du vote diurne. Ainsi, on pourrait particulariser chaque intention de vote en s’assurant que les loups n’ont qu’une faible probabilité de voter contre un des leurs.

On pourrait aussi imaginer une chaîne de Markov qui tiendrait compte, par exemple, des résultats des 2 tours précédents. Si un habitant a désigné et contribué à mettre-à-mort un innocent villageois au tour N, il augmente la suspicion à son égard et donc la probabilité qu’il soit désigné par les villageois au tour N+1. J’aimerais bien avoir un peu de temps pour faire ça.

Le cas particulier à 6 joueurs

Pour terminer concernant l’objet initial de ce billet, dans le cas d’un jeu à 6 joueurs parmi lesquels se cache un loup-garou.

Sur un million de parties selon nos règles simplifiées, les loups gagnent dans 53% des cas.

Le jeu de loups-garous maison

Pour terminer, voici notre réalisation du jeu du loups-garous. J’ai rajouté un loup supplémentaire pour tester.

Le jeu a été un grand succès et je crois que Marie a beaucoup aimé ! On a d’ailleurs été amené par la suite à créer des cartes supplémentaires (Sorcière et Capitaine).