Cet article fait le point sur l’art délicat d’accorder une guitare.

Plan de l’article

Modèle d’une corde vibrante

Dans un premier temps, nous allons modéliser ce qu’il se passe lorsqu’un corde de guitare est pincée.

Soit donc une corde de guitare de longueur $L$, de masse linéique $\mu$ et soumise à une tension $T$. Cette corde est alignée le long de l’axe $e_x$ ainsi que l’illustre la figure ci-dessous. On note $y(x,t)$ la hauteur de la corde à un temps $t$ et en un point situé à une distance $x$ du sillet de tête.

Guitare vue de côté

En faisant un bilan des forces s’appliquant à un élément $\delta l$ de la corde on obtient l’équation de d’Alembert :

\[\frac{\partial^2 y}{\partial x^2} - \frac{1}{v^2} \frac{\partial^2 y}{\partial t^2} = 0\]

Cette équation fait apparaître le paramètre $v$ qui représente la vitesse de propagation de la perturbation le long de la corde :

\[v = \sqrt{\frac{T}{\mu}}\]

Les modes propres de vibration s’écrivent :

\[y_n(x,t) = \sin \left( n \pi \frac{x}{L} \right) \cos \left( n \pi \frac{v t}{L} \right)\]

Toute solution de l’équation de d’Alembert s’écrira comme combinaison linéaire des modes propres :

\[y(x,t) = \sum_{k=1}^{+ \infty} B_n y_n(x,t)\]

Les propriétés typiques des cordes de guitares sont données dans le papier de Woodhouse de 2004 pour des cordes de longueur $L=0.65$ m de la marque D’Addario Pro Arté (voir référence en fin d’article). Les mesures qui nous intéressent dans la suite de l’article sont résumées dans la table ci-dessous (les cordes sont numérotées de la plus aiguë à la plus grave). Nous ajoutons à l’article initial les diamètres des cordes (dans le cas typique d’un jeu 11/52) ainsi que les modules de Young (pris ici tous égaux à celui de l’acier).

Corde 1 2 3 4 5 6
Note $E_4$ $B_3$ $G_3$ $D_3$ $A_2$ $E_2$
Fréquence $f_0$ (Hz) 329.6 246.9 196.0 146.8 110.0 82.4
Tension T (N) 70.3 53.4  58.3  71.2  73.9  71.6
Masse linéique $\mu$ (g/m) 0.38 0.52 0.90 1.95 3.61 6.24
Vitesse de propagation $v$ (m/s) 429 321 255 191 143 107
Diamètre $D$ (mm) 0.28 0.36 0.46 0.71 0.97 1.32
Module de Young $E$ (GPa) 210 210 210 210 210 210

En prenant les caractéristiques de la corde de Mi aigu et en écartant la corde de 1 mm le long de l’axe y au point d’abscisse $x=L/3$, nous obtenons une oscillation de la corde décrite dans la figure ci-dessous (nous n’avons retenu que les 10 premiers modes propres).

Excitation d'une corde

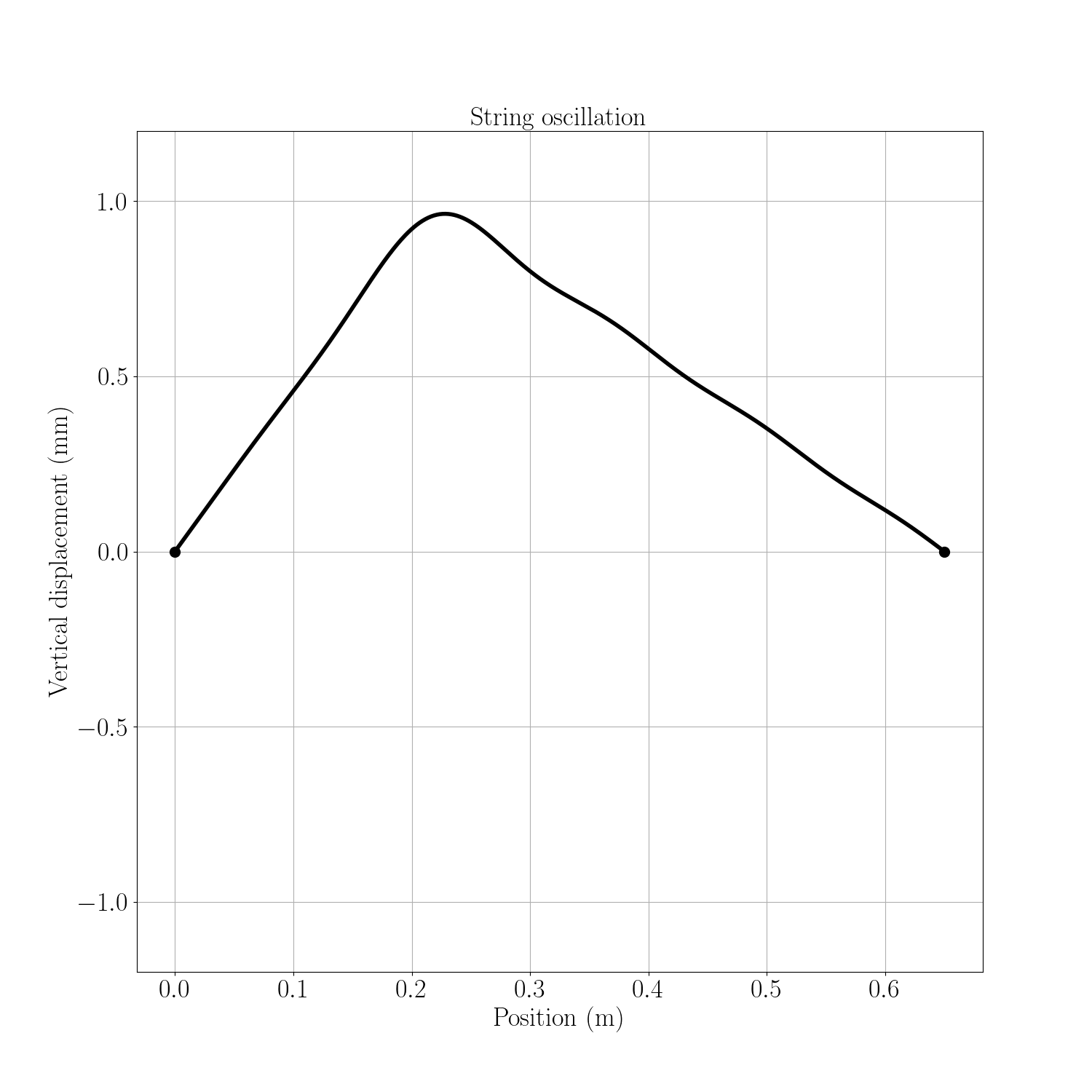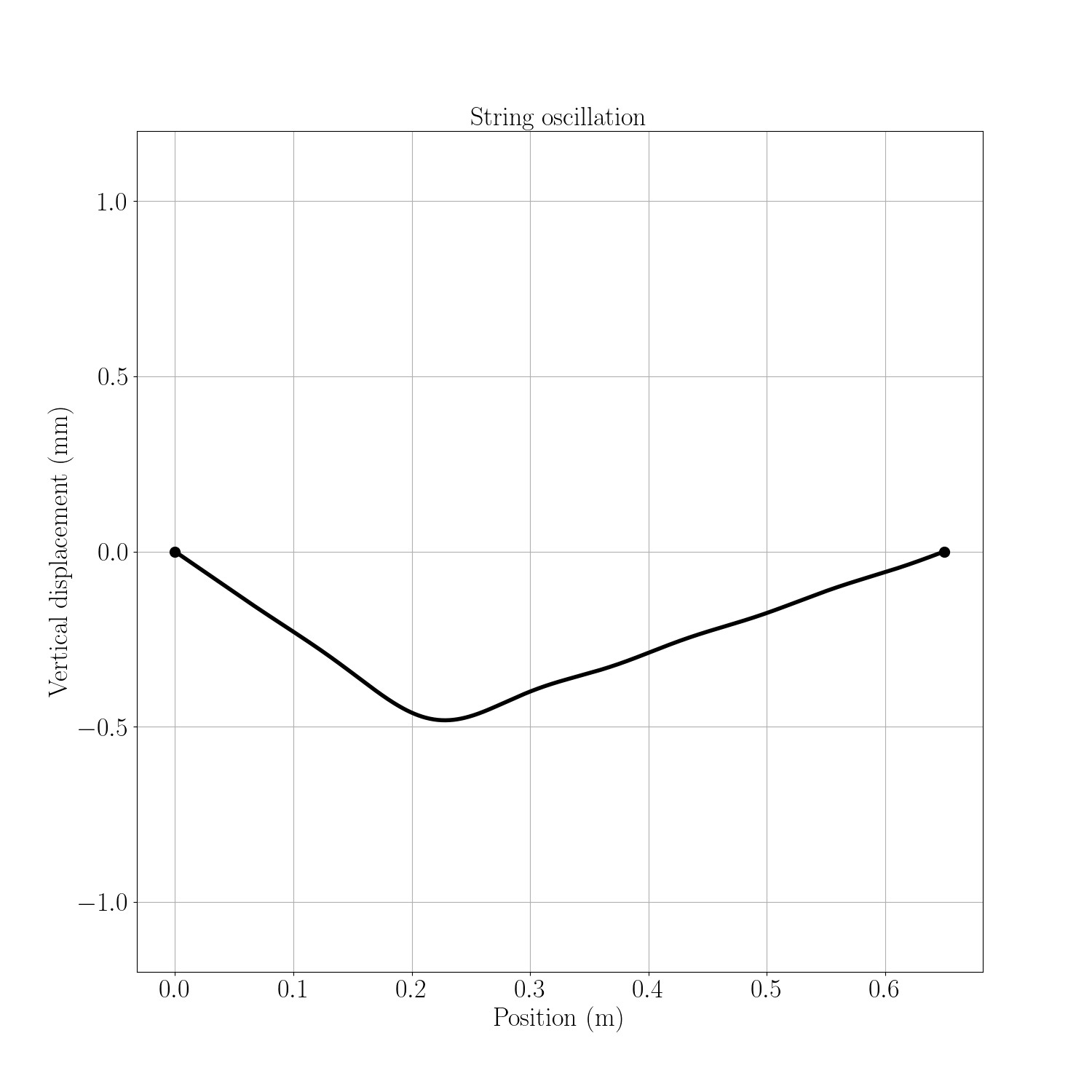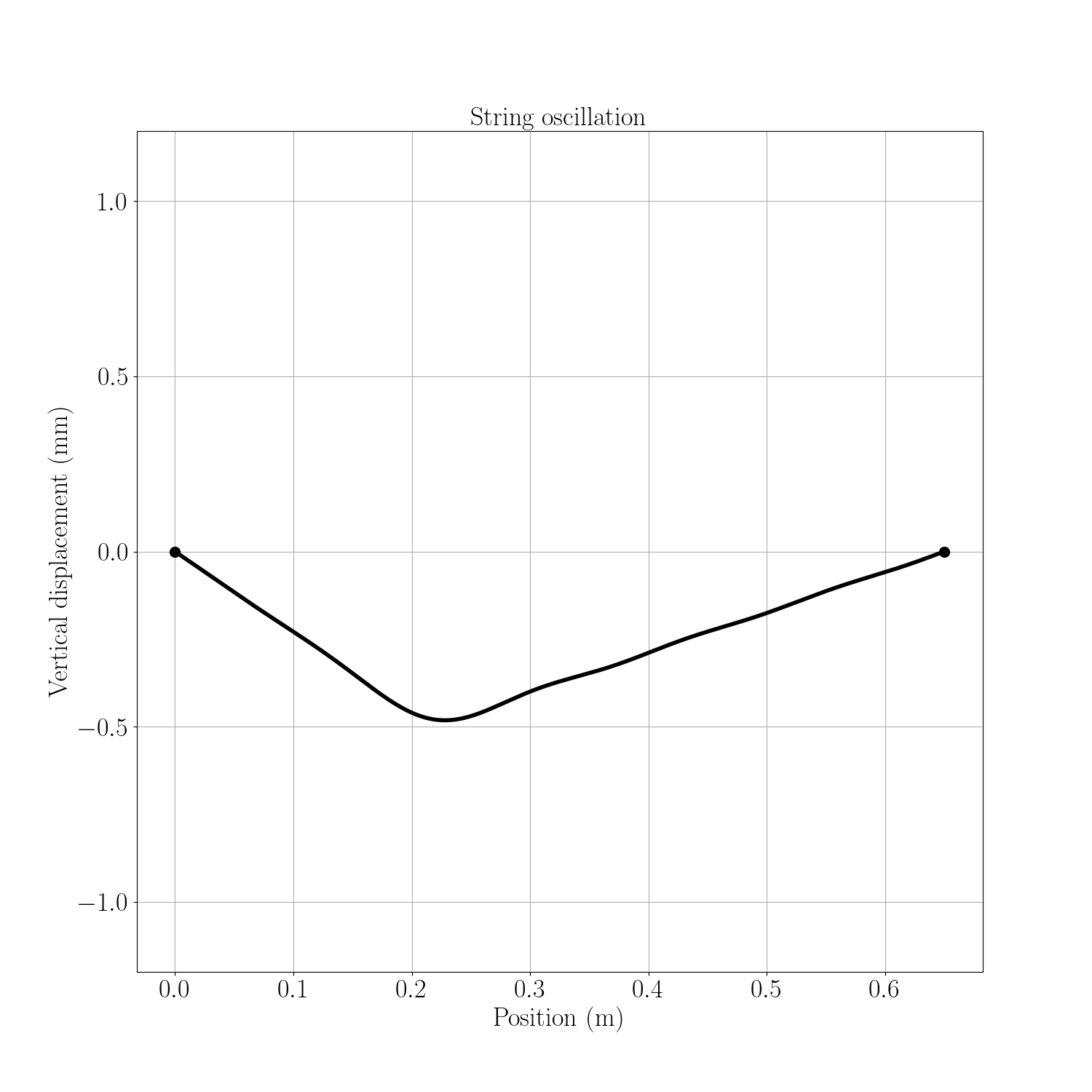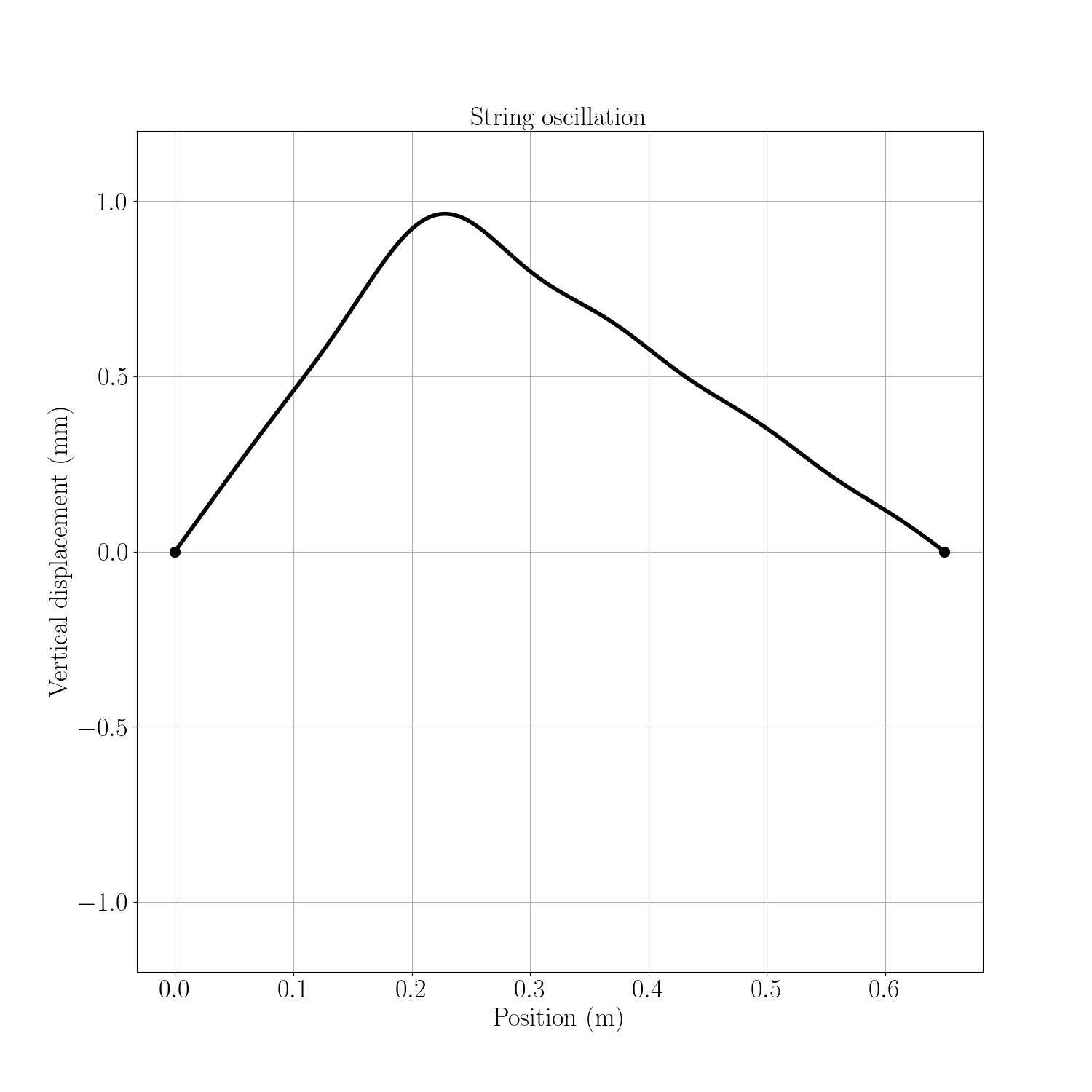
Oscillation d'une corde de guitare

Nous retrouvons cette même évolution dans la vidéo du département de physique de l’Université Kettering. Dans le cas réel, on remarque bien évidemment la présence d’une atténuation de l’onde avec le temps.

Il y a également sur le net une petite application Javascript en ligne qui permet de jouer un peu avec le modèle de corde vibrante. C’est assez bien fait bien qu’on ne puisse pas définir directement les paramètres autrement qu’au jugé.

Accorder sa guitare

Admettons que vous commenciez à accorder votre guitare. Si nous faisons l’hypothèse d’un manche parfaitement rigide, les cordes s’accordent indépendamment les unes des autres et tout se passe bien.

Mais notre manche n’est pas parfait et peut se déformer sous l’effet des contraintes que nous lui appliquons ! Admettons que vous accordiez la première corde. Vous jouez sur sa clef jusqu’à trouver, à l’aide d’un accordeur, la tension à lui appliquer pour obtenir la bonne fréquence. Le matériau du manche va légèrement se déformer sous l’effet de cette contrainte mais au final, cela vous importe peu puisque vous vous basez sur la lecture de votre accordeur pour trouver la condition d’équilibre (c’est-à-dire : la tension pour laquelle la fréquence de vibration est celle souhaitée; en l’occurrence un Mi à 329.6 Hz).

Passez maintenant à la deuxième corde. Vous effectuez la même manipulation mais lorsque vous augmentez la tension de cette deuxième corde, vous allez de nouveau comprimer le manche. Ce faisant, vous vous éloignez des conditions d’équilibre que vous avez obtenu pour la première corde ! Cette dernière ne sonnera plus exactement au Mi mais un peu en-dessous.

Une estimation grossière du facteur de compression

Si on modélise le manche de la guitare comme un pavé de longueur $L = 65$ cm et de côtés respectivement $a=4$ cm et $b=2$ cm, il est possible d’estimer son allongement $\varepsilon$ sous l’effet d’une contrainte $\sigma$ liée à la somme des tensions des cordes. On utilise pour cela la loi de Hooke :

\[\sigma = E \varepsilon\]

Vous avez reconnu le module de Young, noté $E$. Selon les essences du bois constituant le manche, ce dernier varie de 10 GPa jusqu’à 16 GPa. Prenons dans la suite le cas d’un (magnifique) manche en acajou, pour lequel $E = 12$ GPa.

Une petite application numérique nous donne ainsi (en prenant $S=ab$) :

\[\sigma = \frac{-\sum_{k=1}^6 T_k}{S} \approx -4.98 \cdot 10^5\textrm{ Pa}\]

Soit un allongement relatif d’environ $-4.15 \cdot 10^{-5}$. Par rapport à une guitare sans corde, une guitare en acajou correctement accordée verra ainsi son manche raccourcir d’environ 27 µm. Cette valeur est extrêmement petite et nous permet de valider l’hypothèse du manche indéformable. Néanmoins, pour la beauté du geste, nous allons tout de même calculer la façon optimale pour accorder sa guitare en prenant en compte tous les couplages mécaniques.

Accorder sa guitare dans le cas général

Dans le cas général, on considère un manche de module de Young $E$, de section $s$ et de longueur au repos $L_0$ auquel sont raccordées six cordes de module de Young $E_k$, de section $s_k$ et de longueur au repos $l_k$.

Les sept inconnues que sont la longueur du manche encordé $L$ et les six tensions de corde $T_k$ sont données par la relation linéaire suivante :

\[\begin{pmatrix} -1/s & -1/s & -1/s & -1/s & -1/s & -1/s & -E/L_0 \\ \phantom{-}1/s_1 & 0 & 0 & 0 & 0 & 0 & -E_1/l_1 \\ 0 & \phantom{-}1/s_2 & 0 & 0 & 0 & 0 & -E_2/l_2 \\ 0 & 0 & \phantom{-}1/s_3 & 0 & 0 & 0 & -E_3/l_3 \\ 0 & 0 & 0 & \phantom{-}1/s_4 & 0 & 0 & -E_4/l_4 \\ 0 & 0 & 0 & 0 & \phantom{-}1/s_5 & 0 & -E_5/l_5 \\ 0 & 0 & 0 & 0 & 0 & \phantom{-}1/s_6 & -E_6/l_6 \end{pmatrix} \begin{pmatrix} T_1\\ T_2\\ T_3\\ T_4\\ T_5\\ T_6\\ L \end{pmatrix} = - \begin{pmatrix} E\\ E_1\\ E_2\\ E_3\\ E_4\\ E_5\\ E_6 \end{pmatrix}\]

Il suffit d’inverser ce système pour obtenir les tensions $(T_k)$ partant des longueurs à vide $(l_k)$. On obtient ainsi :

\[T_k = s_k\, E_k\, \frac{L - l_k}{l_k}\]

Avec :

\[L = \frac {(\sum_{k=1}^6 s_k E_k) + s E} {(\sum_{k=1}^6 s_k E_k/l_k) + s E / L_0}\]

Il suffit ensuite de remarquer que la fréquence $f_k$ dépend de la tension $T_k$ :

\[f_k = \frac{1}{2L} \sqrt{\frac{T_k}{\mu_k}}\]

Ceci nous donne au final :

\[T_k = 4 L^2\,\mu_k\,f_k^2\]

En injectant ceci dans la première équation du système linéaire, et en notant $\lambda = \sum \mu_k f_k^2$ il vient alors :

\[-\frac{4 L_0^2 \lambda}{sE} \left( \frac{L}{L_0} \right)^2 - \frac{L}{L_0} + 1 = 0\]

Ceci est un polynôme de degré deux en $L/L_0$. En remarquant que son discriminant $\Delta = 1+ 16 L_0^2 \lambda/sE$ est toujours positif, il vient deux racines dont on ne garde que celle qui est physiquement réaliste. A savoir donc :

\[\frac{L}{L_0} = \frac{\sqrt{\Delta} -1 }{8 L_0^2 \lambda} s E\]

Une application numérique nous donne alors $L/L_0 \approx 0.99995$ soit un raccourcissement du manche de 27 µm. Nous retrouvons bien la même valeur que dans notre calcul initial.

On peut introduire les tensions $T_{k,0}$ et la longueur initiale $L_0$ qui sont solutions du cas particulier d’un manche incompressible et qui correspondent aux valeurs limites des équations ci-dessus lorsque $E \to \infty$. Auquel cas, nous avons :

\[T_k = T_{k,0} + \Delta T_k\]

Avec :

\[\Delta T_k = 4 \mu (L_0^2-L^2) f_k^2\]

Ces écarts en tensions $\Delta T_k$, qui prennent donc en compte le couplage mécanique total de l’ensemble du système, sont donnés ci-dessous en N pour les six cordes dans les trois cas suivants :

  1. un manche d’une rigidité infinie : on retrouve logiquement les valeurs mentionnées dans le tableau en début d’article
  2. un manche réel en acajou : on observe bien un écart en tension mais extrêmement petit (de l’ordre de $10^{-3}$ N)
  3. un manche réel en caoutchouc : cette fois-ci l’écart est beaucoup plus marqué avec des variations en tension de l’ordre de la dizaine de N

D’une façon générale, on remarque que les écarts en tension par rapport au cas idéal sont positifs, c’est à dire que $T_k > T_{k, 0}$. C’est attendu puisque $L < L_0$ : pour compenser une diminution de la longueur du manche, il faudra appliquer une tension plus forte sur les cordes. Notons à ce niveau que nous supposons être en régime élastique pour le manche et les cordes et que nous ne dépassons pas les valeurs de rupture. En particulier, j’ignore si la guitare en caoutchouc est réalisable. Avec des tensions de l’ordre de la centaine de Newton, cela représente un poids au niveau du sol d’environ 10 kg ce qui me paraît totalement envisageable…

Corde 1 2 3 4 5 6
$E=+\infty$ 0 0 0 0 0 0
$E=+12$ GPa $+5.78\,10^{-3}$ $+4.44\,10^{-3}$ $+4.85\,10^{-3}$ $+5.89\,10^{-3}$ $+6.12\,10^{-3}$ $+5.94\,10^{-3}$
$E=0.001$ GPa 32.3 24.8 27.0 32.9 34.2 33.1

Cas particulier d’une guitare à deux cordes

Prenons le cas d’un manche en acajou avec uniquement deux cordes de Mi aigu. La figure ci-dessous représente la variation de la fréquence de la première corde en fonction des tensions appliquées aux deux cordes. On voit immédiatement que l’hypothèse d’un manche indéformable est tout à fait valide : la variation en tension de la deuxième corde n’a aucune incidence sur la fréquence de la première corde ! Les trois bandes noires centrées autour de 55 N, 70 N et 78 N délimitent les zones où la fréquence est (respectivement) un Ré, un Mi et un Fa avec une tolérance de plus ou moins un huitième de ton.

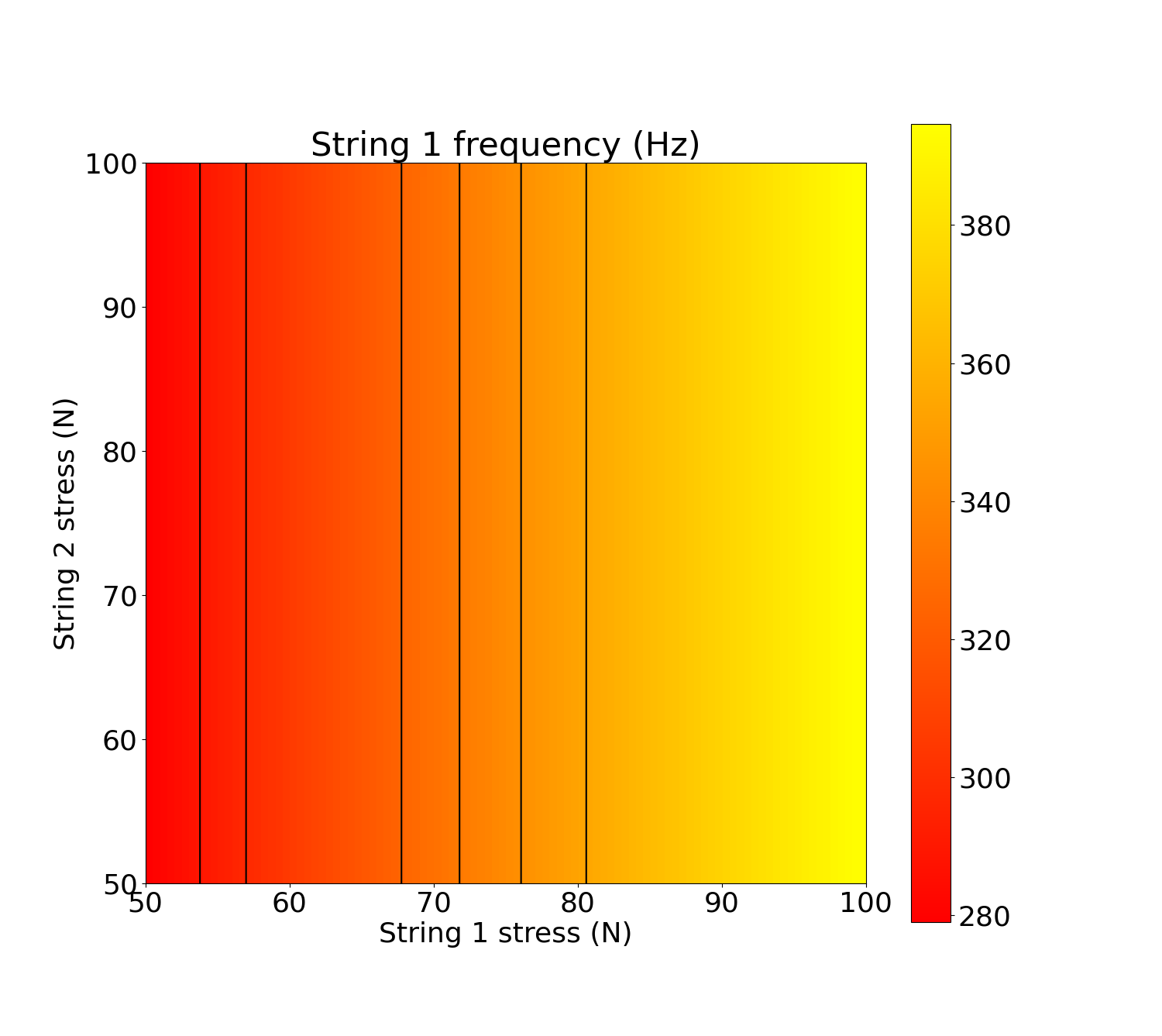
Variation de la fréquence en fonction des tensions des cordes, manche en acajou

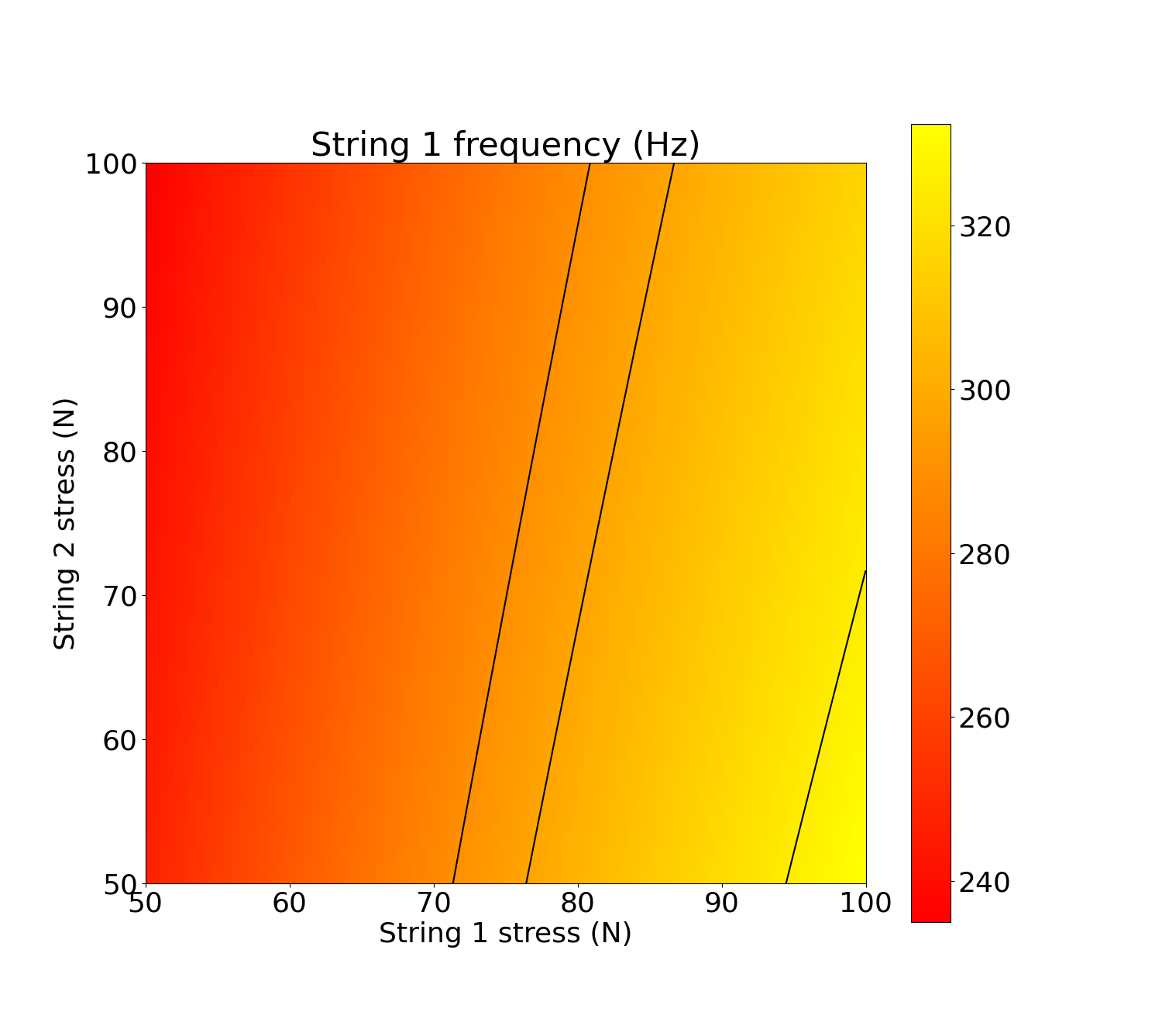
Si on refait l’expérience avec cette fois-ci un manche en caoutchouc, les résultats sont sensiblement différents ! En prenant un module de Young pour le manche de 0.001 GPa, on obtient la figure ci-dessous. Deux points sont notables :

  1. cette fois-ci les deux accordages ne sont clairement plus indépendants ! Une augmentation de tension sur la deuxième corde aura ainsi tendance à faire diminuer la fréquence de la première corde
  2. globalement, à tension égale, les fréquences accessibles sont désormais beaucoup plus petites qu’auparavant. Avec moins de 90 N, on ne peut guère tirer mieux qu’un Ré à 293 Hz.

Variation de la fréquence en fonction des tensions des cordes, manche en caoutchouc

L’idée d’une guitare à deux cordes pourrait prêter à sourire mais en faisant mes recherches pour écrire cet article, je suis tombé sur un bien étrange instrument. Le Đàn bầu est un instrument traditionnel vietnamien. Outre son nom qui me fait bénir la généralisation de l’UTF-8, il présente la particularité d’être un instrument à une seule corde.

La plupart des autres instruments à corde travaillent à tension constante : c’est en faisant varier la longueur de la corde (en appuyant sur les frets) qu’on fait varier la hauteur de la note. Néanmoins, dans le cas du Đàn bầu, l’instrumentaliste influe sur la hauteur en changeant la tension de la corde. Cet instrument est illustré ci-dessous.

Un Đàn bầu

Une anecdote en appelant une autre, certains guitaristes comme Jon Gomm peuvent parfois utiliser les clefs pour faire varier la hauteur des notes pendant qu’ils jouent. C’est assez périlleux car il faut ensuite être en mesure de réaccorder dynamiquement l’instrument.

Vers une modélisation plus réaliste des déformations mécaniques

Nous avons simplifié l’action mécanique des cordes sur le manche en la réduisant à un simple effort en traction/compression. Mais en réalité, l’effort n’est pas appliqué à la verticale du manche mais est légèrement déporté (peut-être d’un cm ?) par l’intermédiaire du sillet de tête. Cela aura tendance à créer un moment fléchissant du manche, un peu à la manière d’un arc qu’on bande.

Influence des conditions extérieures

Une guitare correctement accordée va se désaccorder avec le temps. Néanmoins, j’ai remarqué que ma guitare pouvait parfois rester correctement accordée pendant une longue période en temps (plusieurs semaines) alors qu’en d’autres circonstances il fallait que je la réaccorde tous les deux jours. Comment cela est-il possible ?

Les sources de désaccordage de la guitare pourraient être :

  1. les variations de température (principalement, dilatation des cordes)
  2. les variations d’humidité (gonflement du bois, allongement de la taille du manche)
  3. peut-être dans une moindre mesure, un effet de la pression atmosphérique ?
  4. bien entendu aussi, ma fréquence de jeu
  5. sans oublier ma fille de 2 ans et demi qui s’amuse sporadiquement avec les cordes

De façon très empirique, j’ai ainsi remarqué que les brusques désaccordages de ma guitare semblaient liés à la survenue d’orages.

Avec un peu de temps (ce qui manque le plus !) et si je mets la main sur un hygromètre, je pourrais peut-être tenter de quantifier l’impact de l’humidité sur la hauteur du Mi aigu. Ça serait intéressant de considérer ma guitare comme un convertisseur météo-fréquence…

Références

J. Woodhouse. Plucked guitar transients : Comparison of measurements and synthesis. Acta Acustica United with Acustica, 90 :945–965, 2004.

Elie, Benjamin. Caractérisation vibratoire et acoustique des instruments à cordes-Application à l’aide à la facture instrumentale. Diss. Université du Maine, 2012.