Partage équitable d'une galette des rois
Ce week-end nous avons tiré les rois en famille. Ma fille de quatre ans a naturellement reçu une part plus petite que celles des adultes. Mais en faisant cela, j’ai diminué la probabilité qu’elle trouve la fève, ce qui est un peu injuste.
A quoi ressemblerait une galette des rois qui rétablirait l’équité ?
- Galette des rois traditionnelle
- Galette des rois non uniforme
- Partition d’une galette non-uniforme pour N convives
Galette des rois traditionnelle
Si nous assimilons la galette des rois à un disque unitaire et la fève à un point, alors on peut faire l’hypothèse que cette dernière est uniformément répartie sur la surface de la galette.
En particulier, sa densité de probabilité en fonction de l’angle $\theta$ du répère polaire est une constante égale à $1/2\pi$.
\[f(\theta) = \frac{1}{2\pi}\]La fonction de répartition associée est donc linéaire en $\theta$ :
\[F(\theta) = \frac{\theta}{2\pi}\]Ces deux fonctions sont tracées ci-dessous.
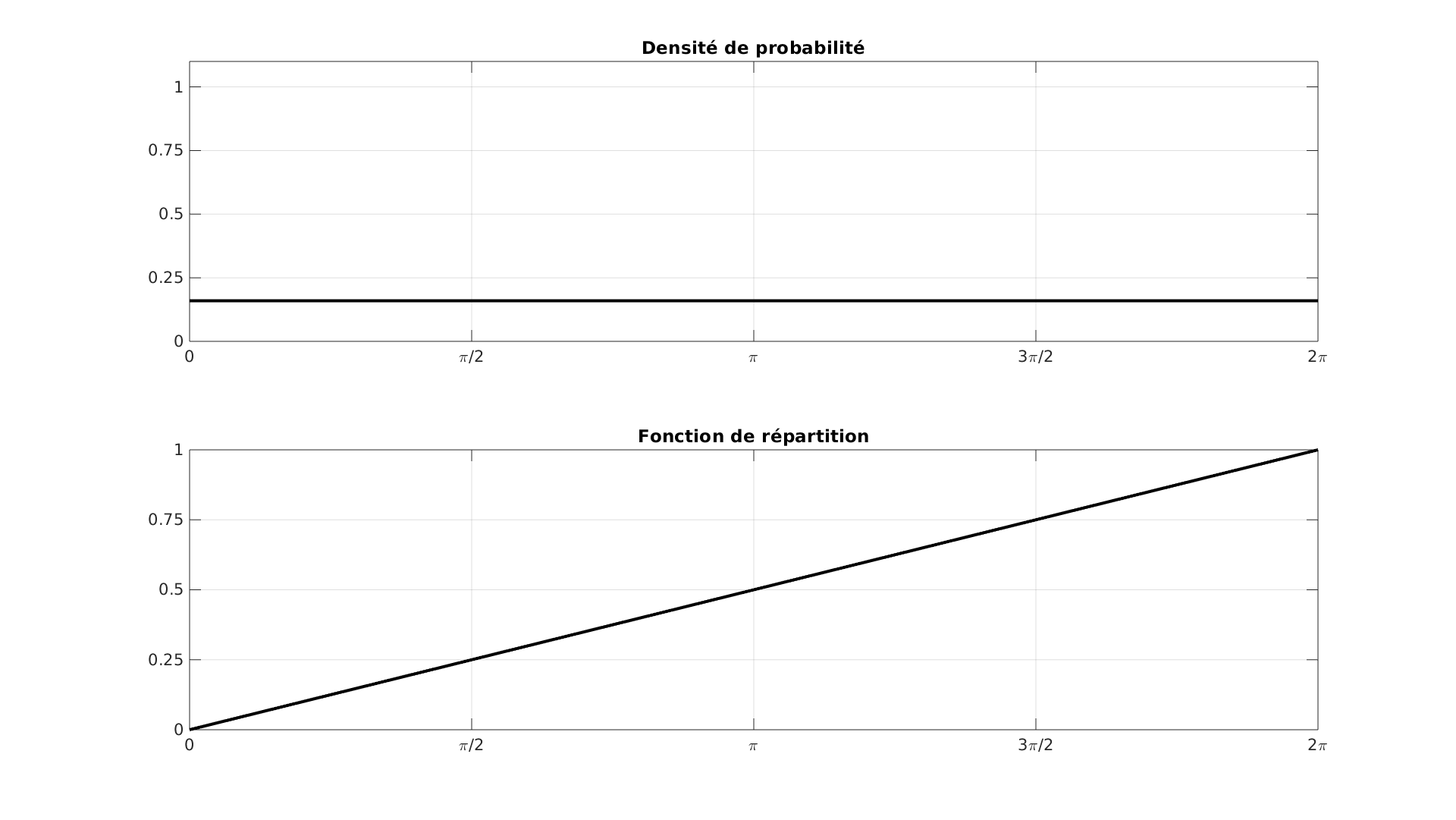
Dans ce cas là, plus la portion de galette est importante et plus élevée sera la probabilité de trouver la fève.
Galette des rois non uniforme
Si maintenant la loi de probabilité n’est plus uniforme, qu’est-ce qu’on obtient ?
Nous pourrions par exemple partir sur un signal triangle défini par :
\[f(\theta) = -\frac{|x-\pi|}{\pi^2} + \frac{1}{\pi}\]La probabilité de trouver la fève sera d’autant plus grande que $\theta$ sera proche de $\pi$, la galette est désormais orientée. Nous avons par ailleurs toujours :
\[\int_{\theta=0}^{2\pi}f(\theta)\,\textrm{d}\theta = 1\]La fonction de répartition associée est un assemblage de deux polynômes de degré 2. Ces deux fonctions sont tracées ci-dessous.
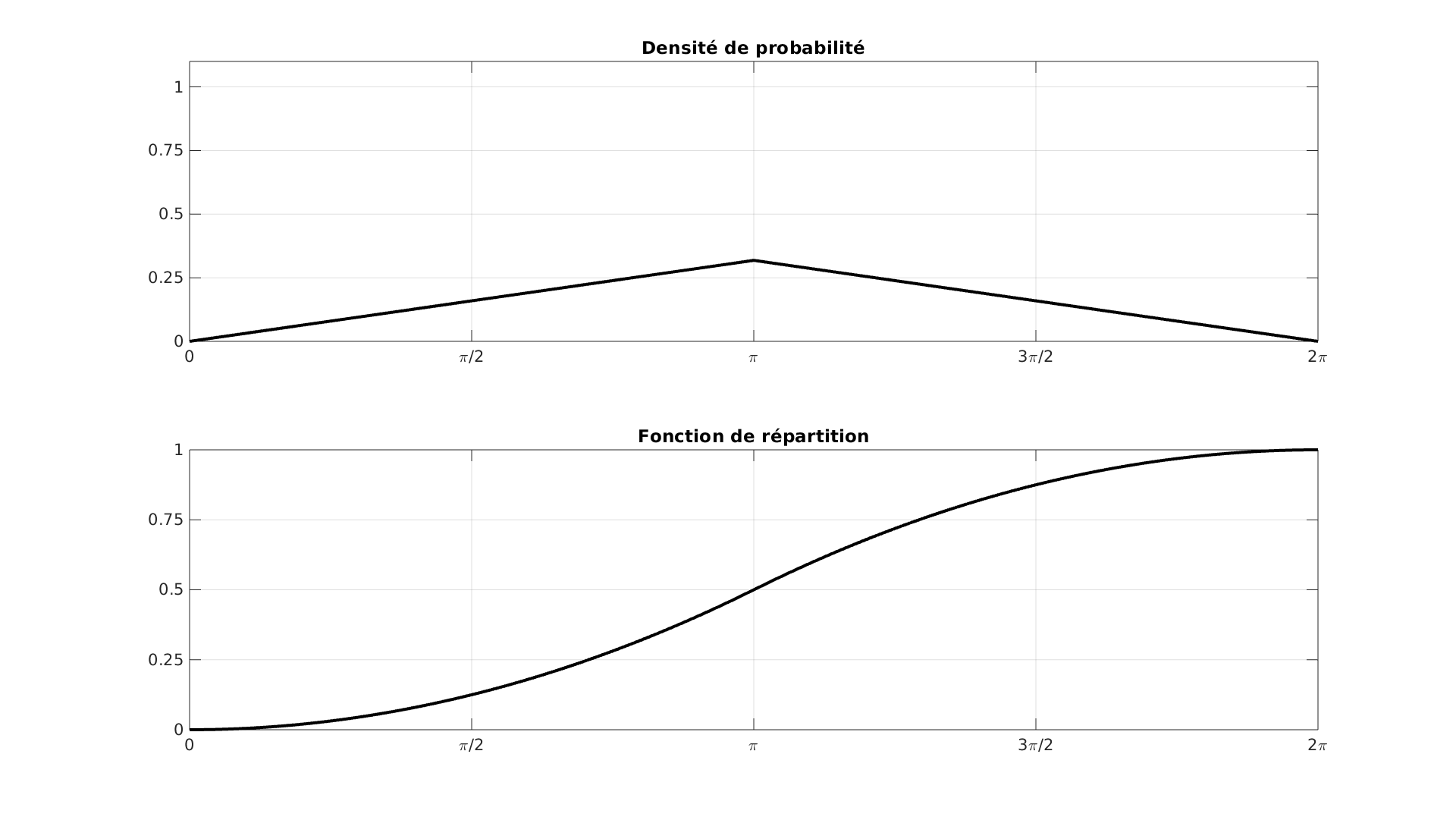
Nous définissons maintenant une part de galette par son angle central $\theta$ et son ouverture angulaire $\epsilon$, tels que définis par la figure ci-dessous.

Alors nous pouvons tracer la probabilité d’obtenir la fève dans une part de galette définie par le couple $(\theta, \epsilon)$. Nous obtenons alors la figure ci-dessous.
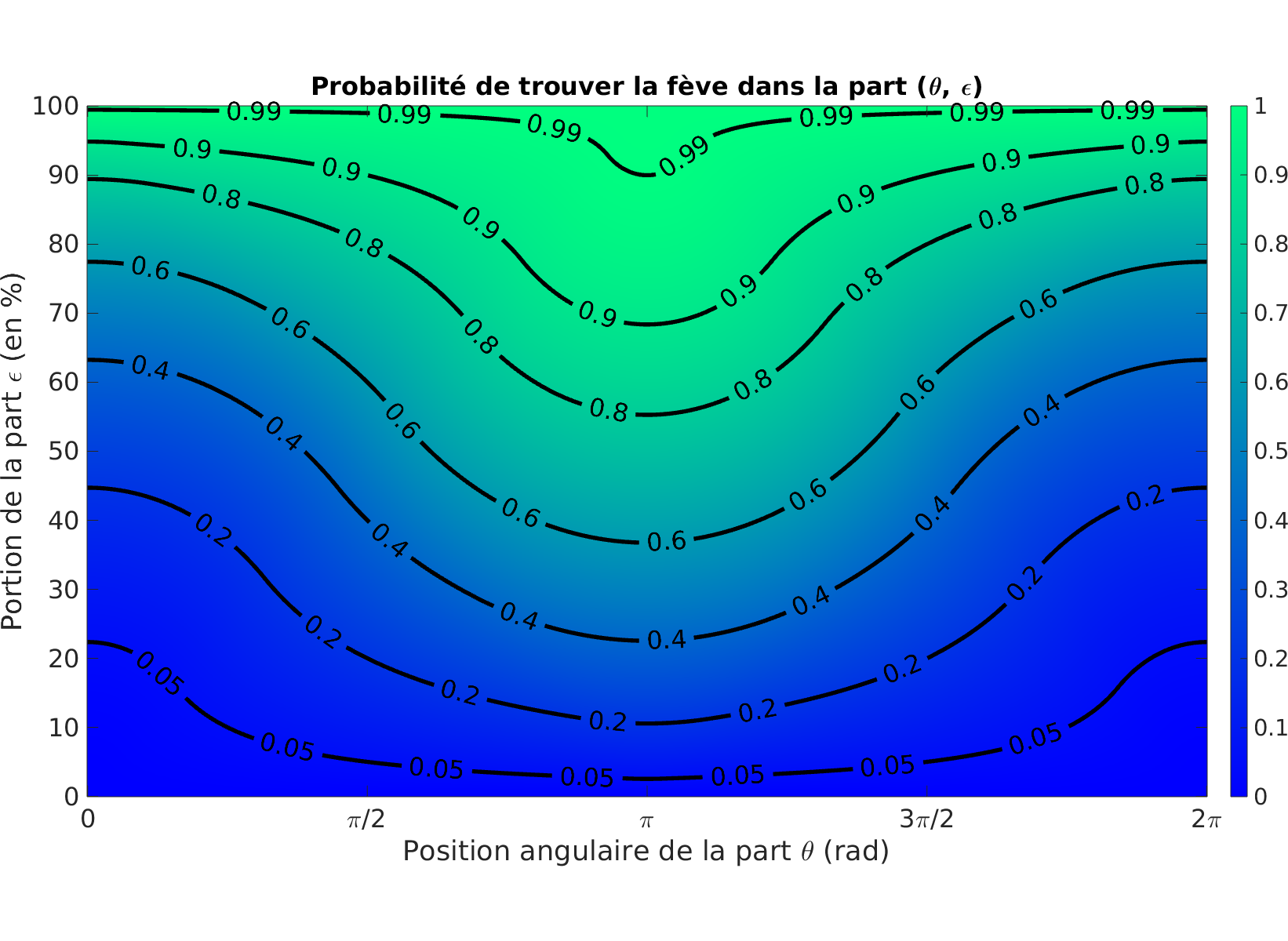
Nous avons également tracé sur cette figure les courbes de niveau de probabilité constante. Ainsi pour avoir 40% de chances d’avoir la fève, on peut choisir une part de galette centrée en $\theta=0$ et d’ouverture angulaire 63% (c’est une grosse part) ou bien se contenter d’une part plus modeste de 22% centrée en $\pi$.
Pour avoir un partage équitable, non pas en proportion de galette mais en probabilité d’obtenir de fève, il suffit alors pour $N$ convives de choisir chacun une part sur la même ligne de niveau de la figure. Il faudra toutefois garder en tête que les parts ne doivent pas se recouvrir !
Partition d’une galette non-uniforme pour N convives
Si maintenant nos $N$ convives souhaitent se partager la galette non-uniforme afin d’avoir chacun la même probabilité d’obtenir la fève, qu’est-ce qu’on obtiendrait ?
Un petit calcul sur la fonction de répartition nous permet d’obtenir un découpage qui fonctionne.
Si le nombre $N$ de convives est pair, alors il faut couper la galette à l’angle $\pi$ puis aux $N-2$ angles $\pi \pm \theta_k$ définis par :
\[\theta_k = \pi \left( 1 - \sqrt{1-\frac{2k}{N}}\right)\qquad 1 \leq k \leq \frac{N-2}{2}\]Si le nombre de convives est impair, alors il faut couper la galettes aux $N-1$ angles $\pi \pm \theta_k$ définis par :
\[\theta_k = \pi \left( 1 - \sqrt{1-\frac{2k-1}{N}}\right)\qquad 1 \leq k \leq \frac{N-1}{2}\]La figure ci-dessous représente de tels découpages pour un nombre de convives variant de 2 à 7. La galette est toujours placée dans le repère polaire traditionnel, l’angle $\pi$ est donc situé à l’extrème gauche de la galette (c’est sans surprise à cet endroit que les parts sont les plus étroites).
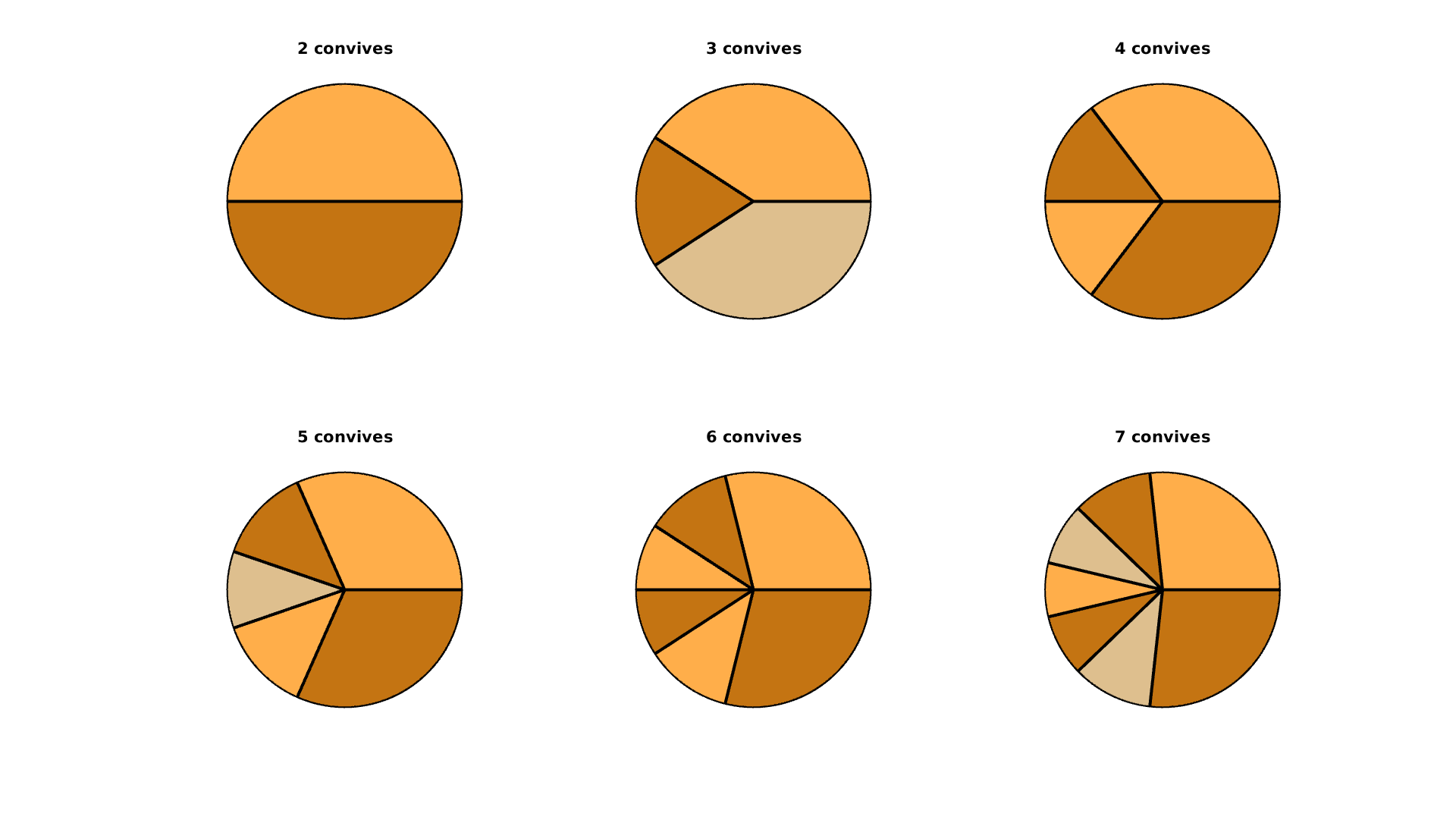
Cette méthode permet donc aux convives d’avoir des parts de différentes tailles tout en garantissant une équité dans la probabilité de gain. Les deux inconvénients sont que d’une part la galette est désormais orientée et d’autre part, la partition est entièrement prédéterminée par la loi de probabilité. Si nos convives émettent des souhaits de partitions a posteriori, il nous sera potentiellement impossible de satisfaire leurs revendications.
Une autre méthode consisterait alors à découper la galette PUIS à sélectionner aléatoirement et de façon uniforme une part parmi les $N$ pour y placer discrètement la fève.