Vertige d'un footballeur
Hier, le mardi 9 juillet 2024, j’ai regardé le match France-Espagne de la coupe d’Europe.
A un moment, s’est affiché rapidement la disposition des joueurs français, avec un titre du genre “3-4-3”.
Alors je sais qu’il s’agit de la répartition des joueurs entre la défense (à gauche) et l’attaque (à droite). Mais en fait, il existe plein de façons différentes de disposer 10 joueurs sur le terrain.
Combien exactement ? C’est l’objet de ce billet de blog.
- Le problème
- La résolution
- Exploration de l’intégralité des tactiques possibles
- Deux résonances
- Liens pour approfondir
Le problème
Donc en fait, il nous faut trouver de combien de façons différentes nous pouvons écrire 10 comme somme d’une suite d’entiers tous strictement positifs.
Par exemple nous avons $3+4+3 = 10$.
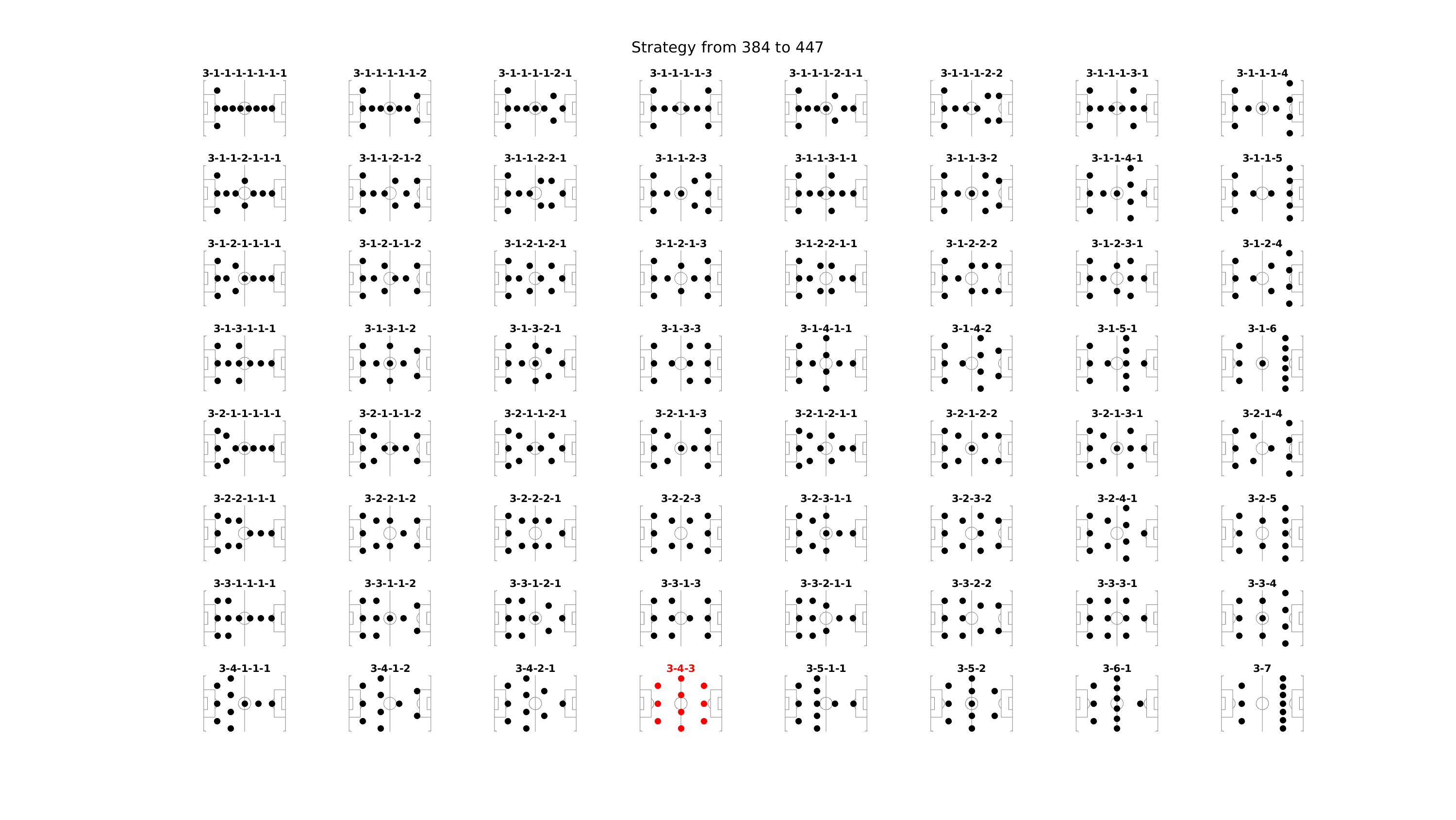
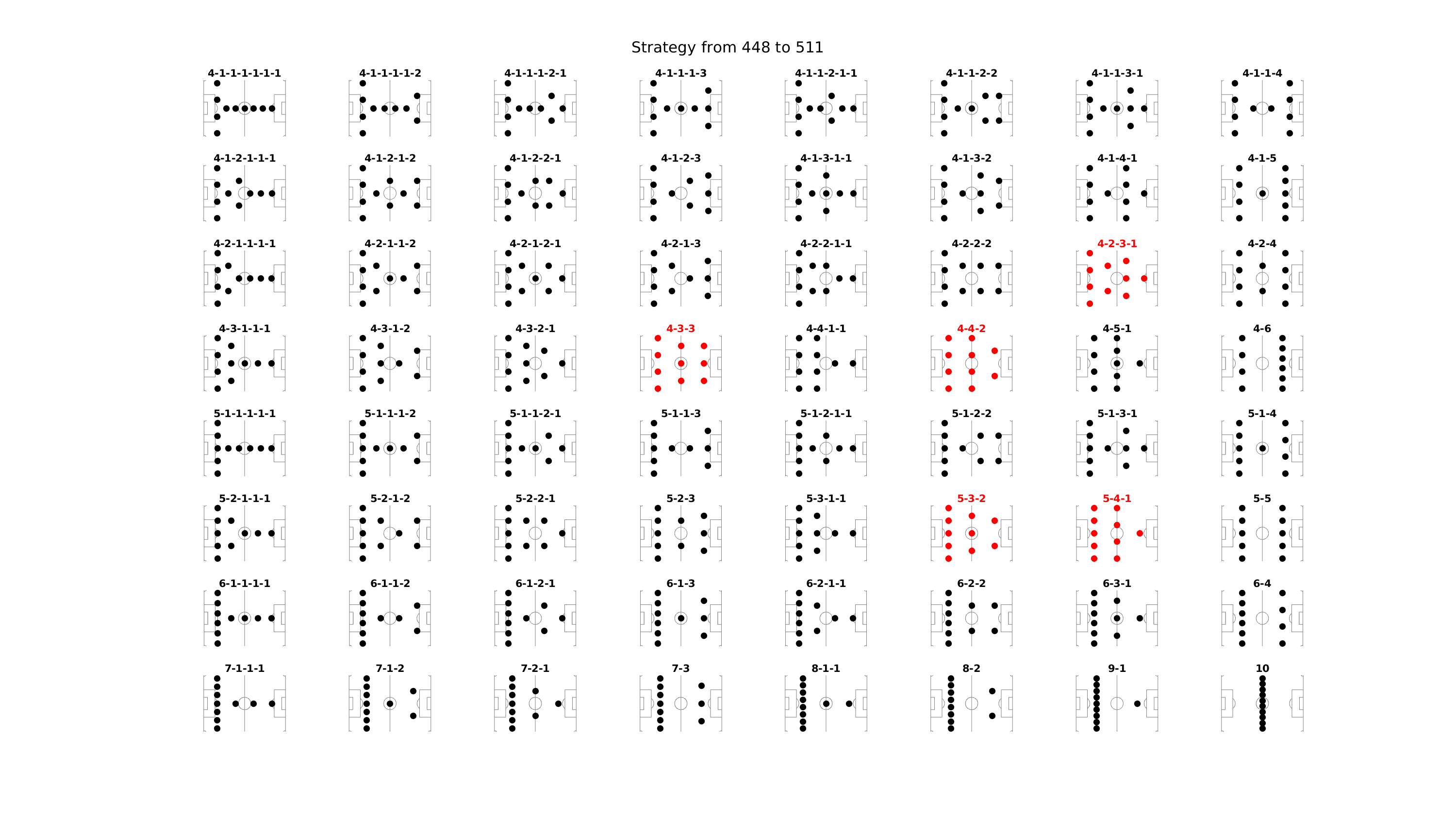
La page Wikipédia dédiée aux tactiques du football en dénombre au total 6, dans la version moderne du football. Ces dispositions sont :
- $4+4+2=10$
- $4+3+3=10$
- $4+2+3+1=10$
- $5+3+2=10$
- $5+4+1=10$
- $3+4+3=10$
Mais on sens bien qu’il y en a plein d’autres.
Quid par exemple de la configuration $1+1+1+1+1+1+1+1+1+1 = 10$ où tous les joueurs seraient alignés à la queue leu-leu sur une longueur du terrain ?
Quid également de la configuration $10=10$ où cette fois-ci tous les joueurs seraient alignés sur une largeur du terrain et présenteraient, pour ainsi dire, un front uni face à l’équipe adverse ?

La résolution
Répondre à cette question de dénombrement revient mathématiquement à s’interroger sur la composition des entiers. La page Wikipédia sur le sujet en parle très bien et avec de très jolis schémas. Je ne vais pas tout détailler mais simplement énoncer les faits qui me paraissent intéressant.
D’une façon générale, le nombre de compositions $c(n)$ d’un entier $n$ est égal à :
\[c(n) = 2^{n-1}\]Dans notre cas de figure avec $n = 10$ joueurs, cela nous donne donc $2^9 = 512$ tactiques différentes.
Il s’agit bien entendu d’un nombre prenant en compte toutes les permutations : $4+3+3$ est différent de $3+4+3$ par exemple.
Si on ne souhaitait pas comptabiliser les permutations, alors le problème revient à calculer le nombre de partitions d’un entier, qui est un problème voisin très bien documenté également sur Wikipédia.
La formule générale qui donne le nombre de partitions $p(n)$ est assez complexe et n’a été obtenue qu’en 1937, par le mathématicien Hans Rademacher. Sa formule fait intervenir les suites de Farey, les cercles de Ford et l’analyse complexe !
Les premiers termes de la suite $p(n)$ apparaît dans l’OEIS sous l’identifiant A000041. Hardy et Ramanujan en ont donné de leur côté une approximation asymptotique :
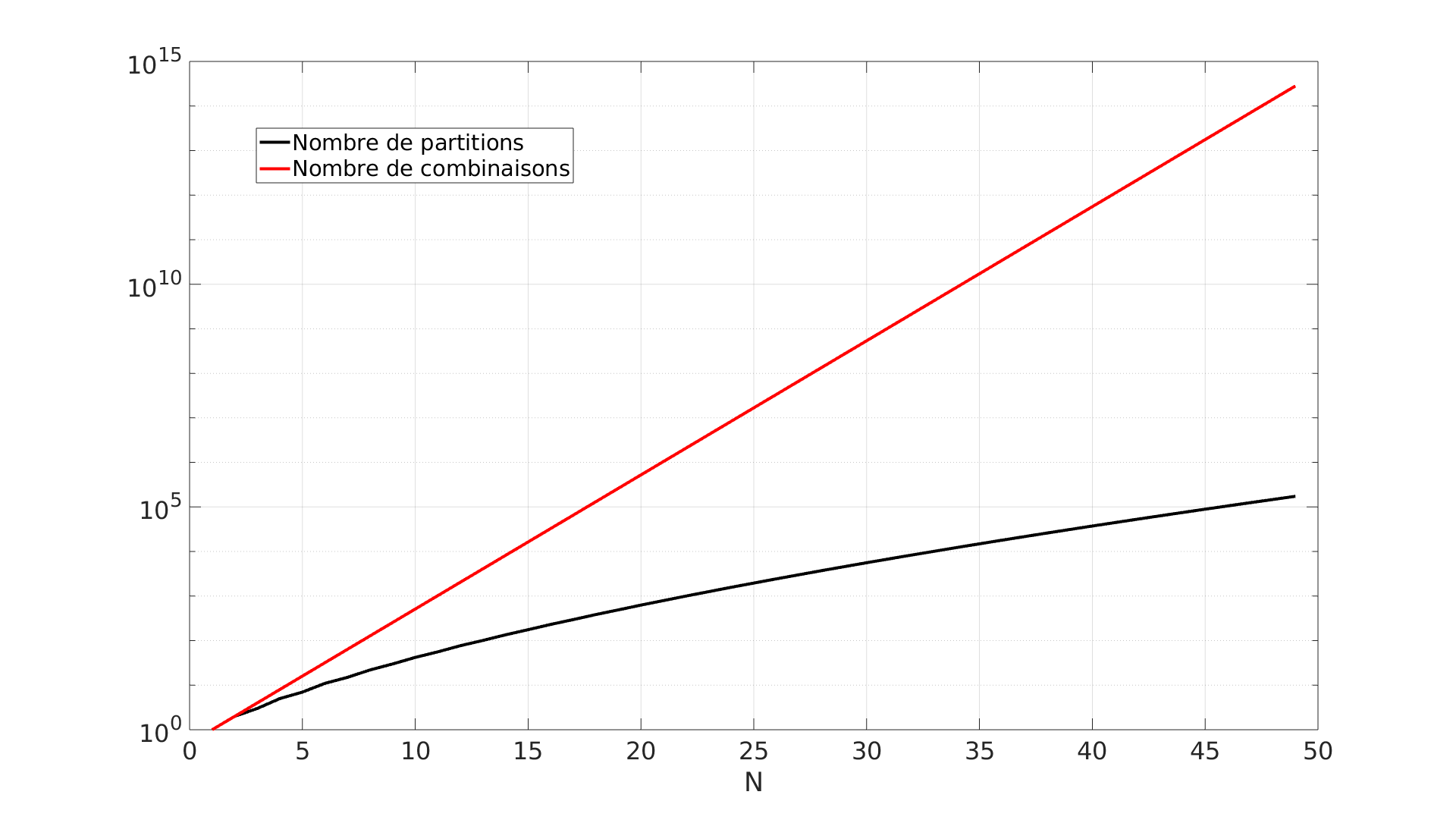
\[p(n) \sim \frac{1}{4n \sqrt{3}} exp \left(\pi \sqrt{\frac{2n}{3}} \right)\]J’ai tracé ci-dessous l’évolution du nombre de partitions (en noir) et de combinaisons (en rouge) pour $N<50$. L’échelle est logarithmique, on voit que le nombre de combinaisons croît beaucoup plus vite !
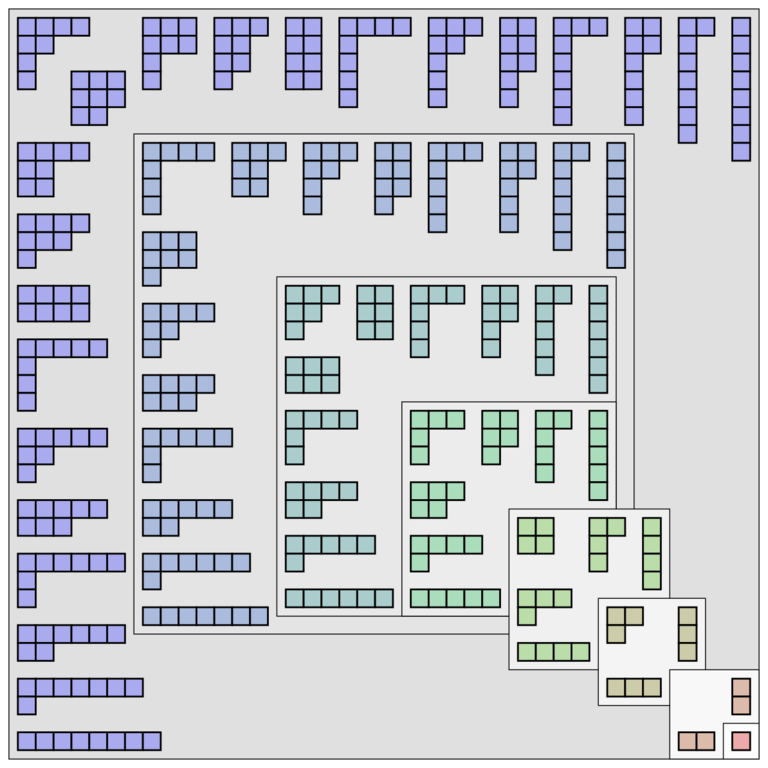
Pour terminer la présentation rapide des nombres de partitions, les diagrammes de Ferrers peuvent aider à visualiser les différentes possibilités de façon très schématique. Ci-dessous le cas pour $n=8$
Exploration de l’intégralité des tactiques possibles
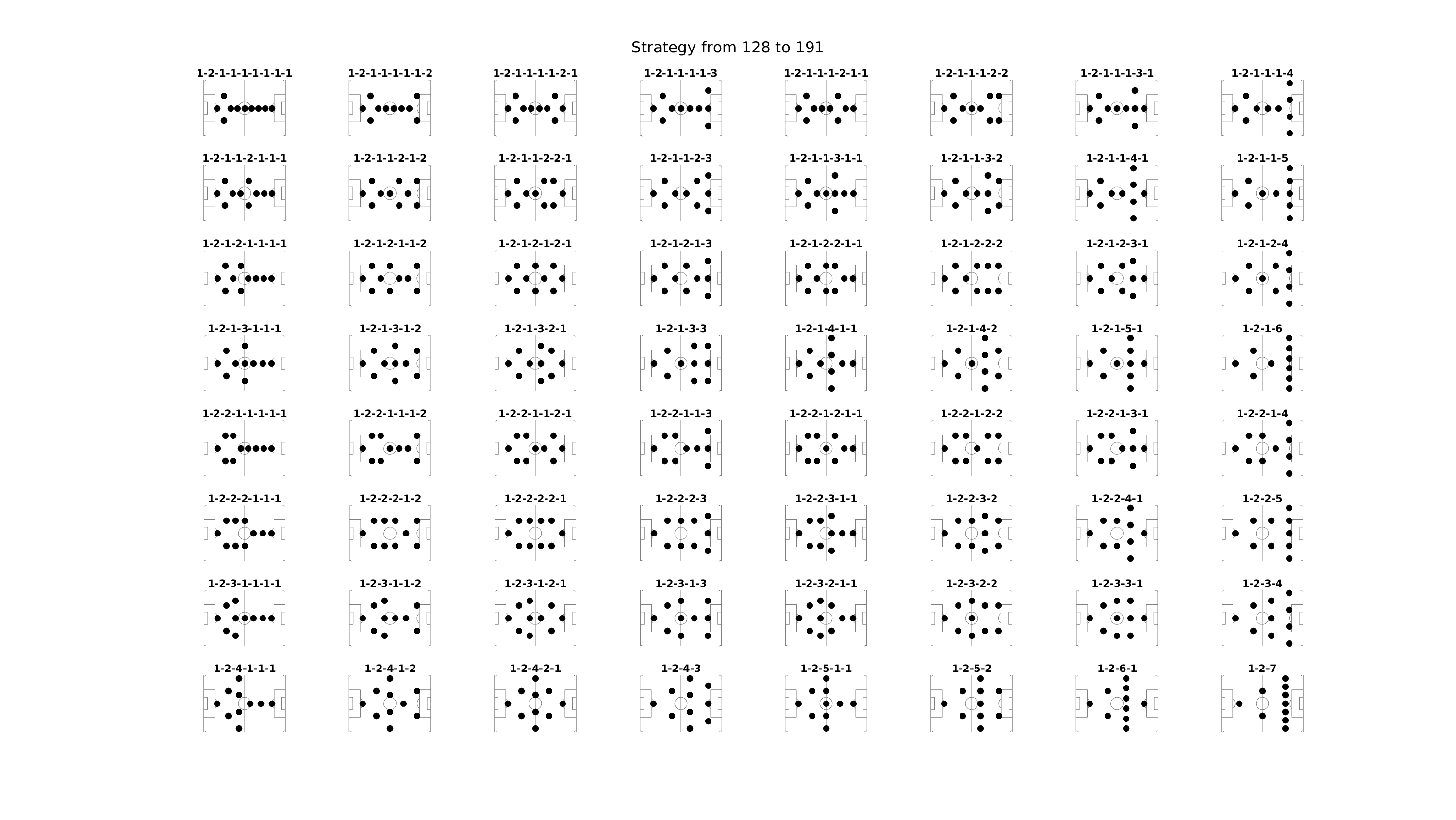
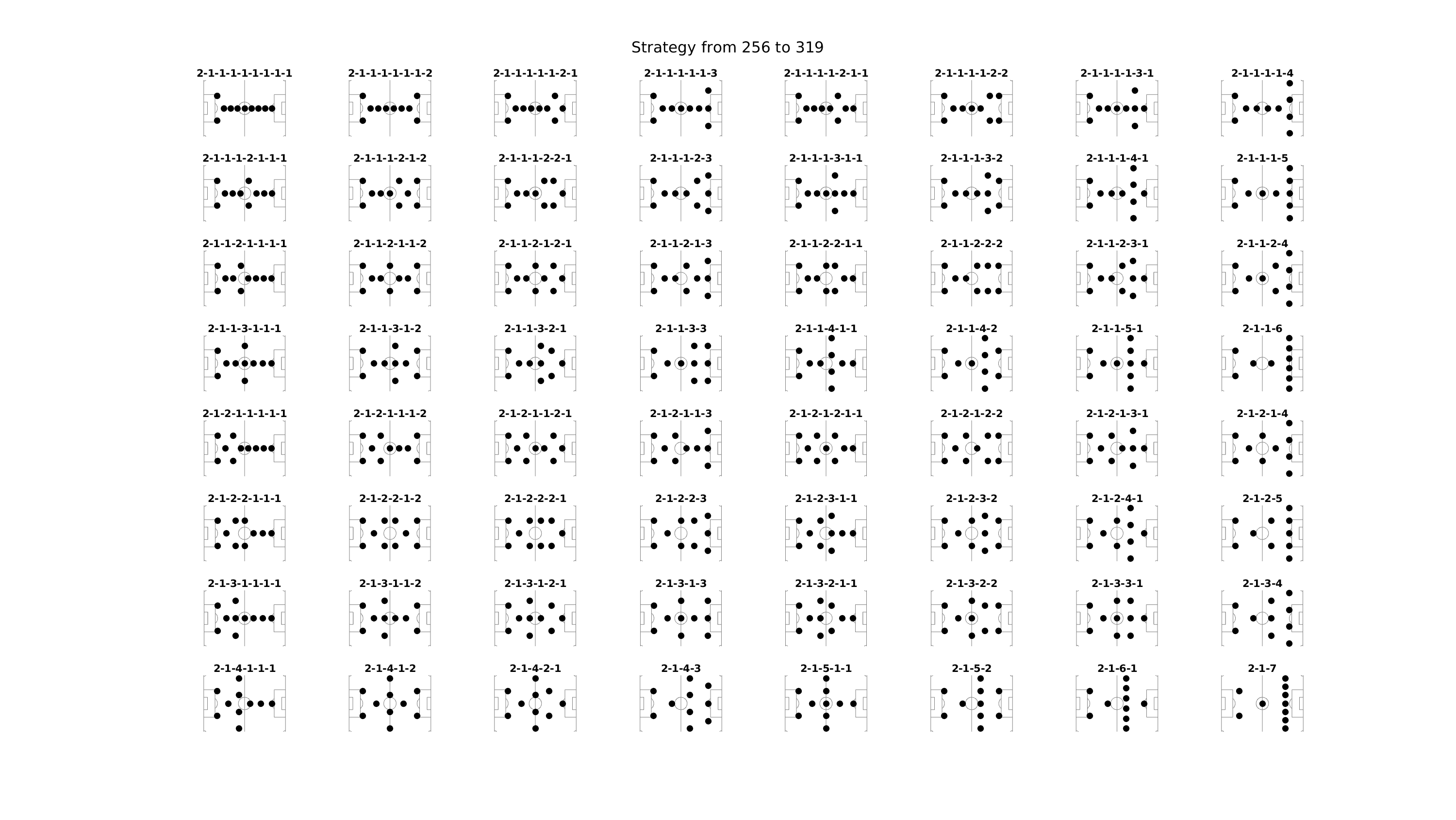
Il existe une façon très élégante d’énumérer toutes les dispositions possibles en se basant sur l’écriture binaire des entiers de $0$ à $2^9$. Je me suis basé sur cette bijection pour établir les schémas exhaustifs du placement des joueurs.
Par exemple, pour avoir la configuration n°167, on remarque que
$167 \equiv 010100111|_{\textrm{bin}}$
On compte ensuite le nombre de 1 (potentiellement nul) entre deux 0 qui se suivent en partant de la gauche.
Dans notre cas de figure, on compte cinq groupes :
- un premier groupe ne contenant pas de chiffre 1 : $\textcolor{red}{*}010100111$
- un deuxième groupe contenant 1 fois le chiffre 1 : $0\textcolor{red}{1}0100111$
- un troisième groupe contenant 1 fois le chiffre 1 : $010\textcolor{red}{1}00111$
- un quatrième groupe ne contenant pas de chiffre 1 : $01010\textcolor{red}{*}0111$
- un cinquième groupe contenant 3 fois le chiffre 1 : $010100\textcolor{red}{111}$
La séquence des tailles de groupe est donc ici $(0, 1, 1, 0, 3)$. On ajoute 1 à chaque élément pour obtenir in fine la configuration $1+2+2+1+4 = 10$.
Ca parait un peu artificel comme procédé, mais il faut se dire que les 0 qui apparaissent dans l’écriture binaire jouent le rôle de délimiteurs entre les joueurs de football.
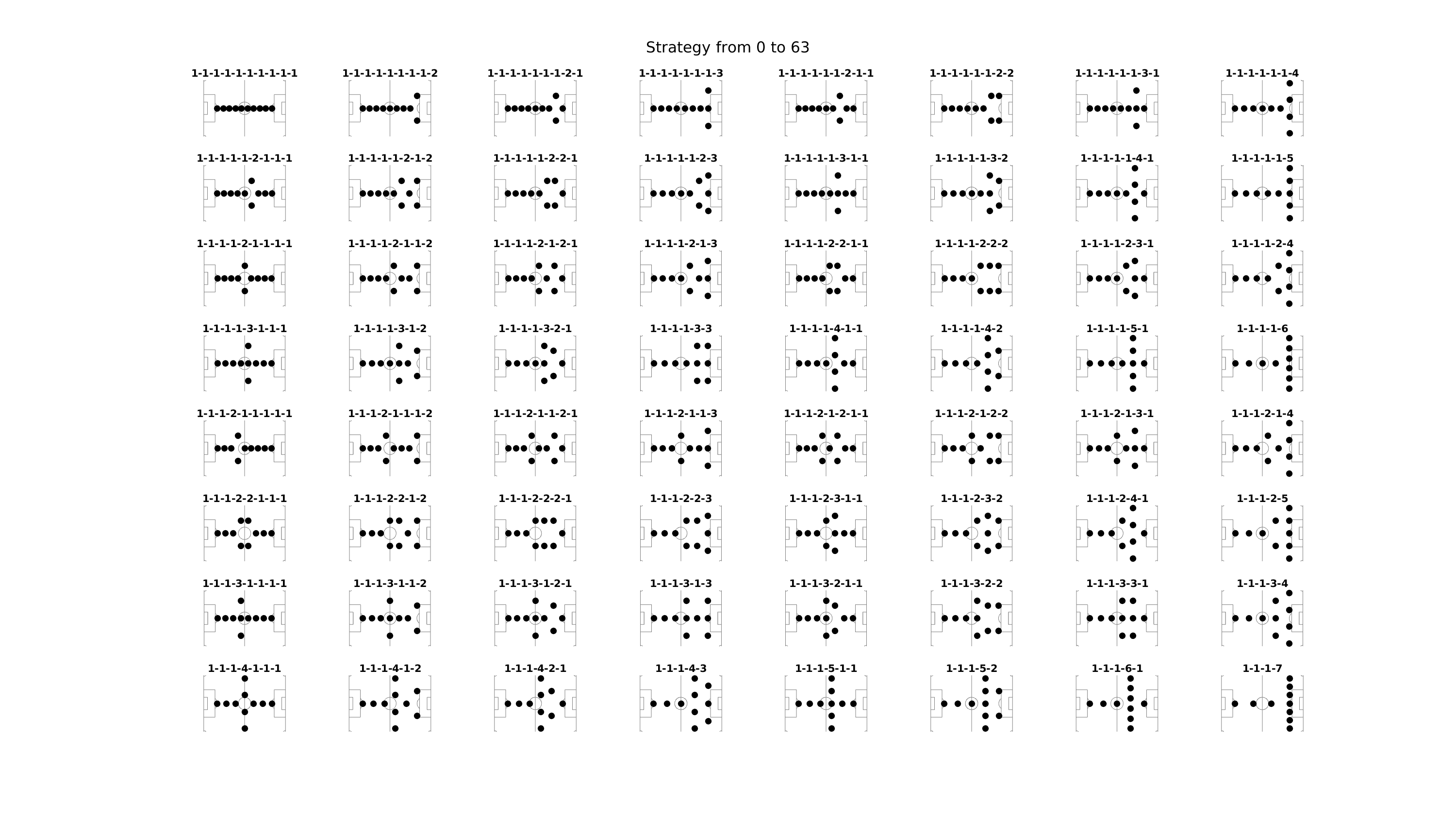
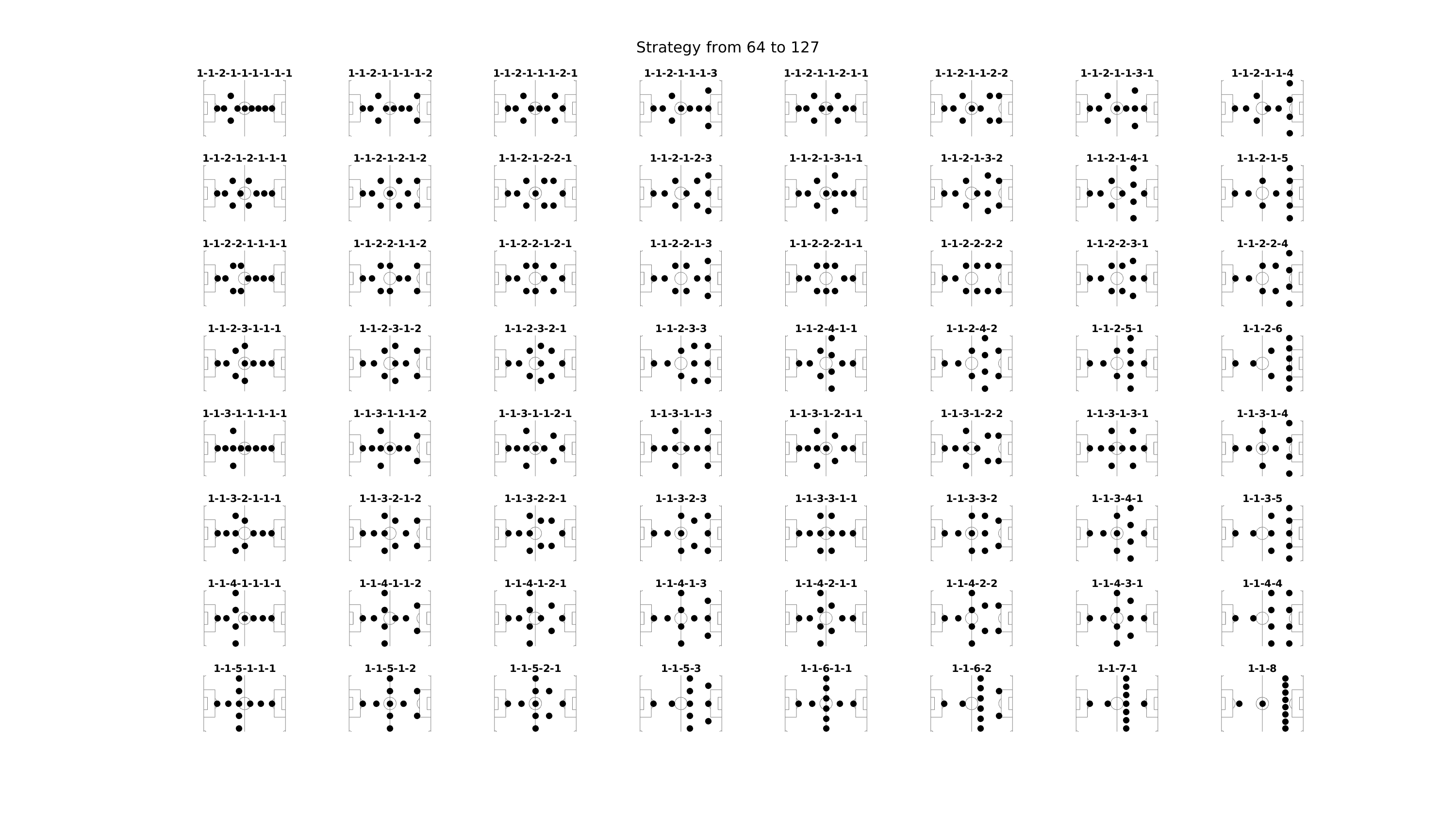
Voici quoiqu’il en soit ce que me génère mon programme d’exploration des 512 tactiques différentes, regroupées par paquets de 64 tactiques. En rouge, les 6 tactiques qui sont mentionnées par la page Wikipédia précemment citée. Pour les voir en grand :


Deux résonances
Ces petites figures m’ont rappelées le tableau “Vertige d’une chaise” de Max Charvolen, tableau que j’aime beaucoup.

La capture d’écran est de mauvaise qualité et provient du catalogue de l’artothèque de la CMCAS de la ville de Nice.
Je me souviens m’être demandé à une époque s’il était possible de créer un “générateur de chaises” à partir des quelques 720 réalisations proposées par Charvolen. Mais le processus ne me semble pas évident. De mémoire, j’espérais une superposition de projections de chaises dont on aurait fait varier l’orientation (rotation) ou la dimension (homothétie). Mais ça semble plus complexe que cela, et il y a des perturbations sur la structure même de la chaise. Du coup, j’ai un peu laissé tomber. Mais cet article me permet de me souvenir de ce truc là tiens. Le résultat final du tableau fait penser à une écriture à base de sinogrammes.
Par ailleurs, régulièrement quand je me prête au jeu de dénombrer pour le simple plaisir de le faire, je repense toujours à Georges Perec qui disait :
Rien ne semble plus simple que de dresser une liste, en fait c’est beaucoup plus compliqué que ça n’en a l’air : on oublie toujours quelque chose, on est tenté d’écrire etc., mais justement un inventaire, c’est quand on écrit pas etc.
Le plaisir de la combinatoire mathématique, c’est justement quand on refuse d’écrire etc.