Il y a quelques temps, j’ai offert à ma fille ainée le jeu de société “Gagne ta Maman” (qui existe aussi en une version identique “Gagne ton Papa”).

Dans ce jeu, il faut remplir le plus rapidement possible un espace rectangulaire initialement vide à l’aide de polyominos. Formellement, un polyomino est une réunion connexe (i.e. en un seul morceau) de carrés unitaires, ces carrés se touchant par un côté entier.

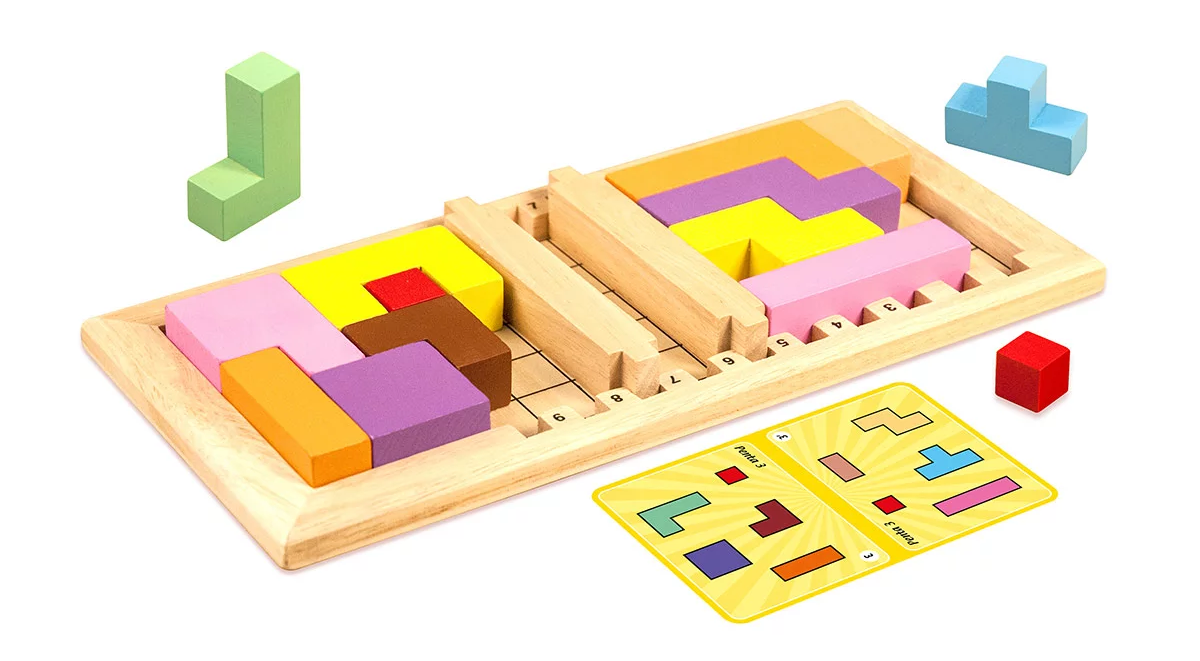
Le jeu Gagne ton Papa / ta Maman

Ce qui est très appréciable dans “Gagne ta Maman”, c’est que la difficulté s’adapte entre parents et enfants, ces derniers devant ainsi paver le rectangle avec des formes plus “simples” que celles des parents. Ou alors le rectangle des parents est initialement plus grand que celui des enfants.

Dans une variante du jeu, appelée les défis 3D, il faut constituer une figure géométrique tri-dimensionnelle (habituellement un cube ou un pavé) à l’aide d’un sous-ensemble prédéfinis de ces polyominos1.

Dans un cas comme dans l’autre, je me suis rendu compte que mon algorithme instinctif de résolution était assez ruste : je procédais un peu par essai-erreur sans vraiment de méthode, en suivant l’intuition du moment. La plupart du temps, ça finissait par rentrer et je m’étonnais des performances de cette heuristique naïve.

Quelques rares fois pourtant, mon procédé ne terminait pas et j’avais l’impression d’arpenter un labyrinthe en aveugle sans jamais pouvoir trouver une sortie. Parfois j’avais l’impression de m’y perdre : cette configuration là n’a-t’elle pas déjà été testée précedemment ?

Depuis, j’ai eu l’occasion de creuser un peu la question et je me rends compte qu’algorithmiquement le problème revient bien à parcourir un (très grand) labyrinthe avec un nombre fini de sorties. Je trouve a posteriori que cette analogie est finalement assez profonde, comme nous le verrons.

Quoiqu’il en soit, cette question là traînait un peu dans un coin de ma tête et puis je l’avais oublié… Jusqu’à ce jour où un ami, à qui j’avais suggéré ce jeu pour son fils, me sollicite sur les réseaux sociaux à propos d’un défi 3D qu’ils n’arrivaient pas à résoudre. Je l’ai tenté et m’y suis moi aussi cassé les dents. Il s’agit du défi 28 où l’on doit reconstituer un cube $3\times 3 \times 3$ à l’aide des 7 polyominos suivants (un monomino, 4 tétraminos et 2 pentaminos) :

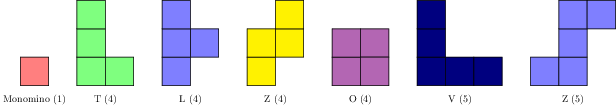
Les 7 polyominos du défi 28

La carte du défi 28

Nous avons bien $1+4+4+4+4+5+5 = 27 = 3^3$ ce qui est une condition nécessaire (mais pas suffisante) pour que le problème ait une solution.

Après bien des essais, j’ai enfin convergé vers UNE des multiples solutions de ce problème (voir ci-dessous). J’ai aussitôt averti mon ami et je me suis dit “plus jamais ça”, il faut que je comprenne comment résoudre ce genre de problème.

Solution du défi, photo 1

Solution du défi, photo 2

Je détaille ici quelques éléments pour systématiser la résolution de tels problèmes. Ca part vite dans tous les sens, j’espère réussir à en tirer quelques lignes claires.

Le problème du recouvrement

La résolution du défi 28, comme le jeu standard “Gagne ton Papa/ta Maman” à base de rectangles à paver, rentre dans le cadre d’une vaste classe de problèmes mathématiques appelée problème du recouvrement.

Le problème des huits dames en est un exemple classique, de même que le cube Soma.

Au début des années 2000, le mathématicien Donald Knuth a développé un algorithme pour résoudre ces problèmes dans le cas général. Sa solution s’appelle l’algorithme X et il en a proposé une implémentation astucieuse grâce aux liens dansants. Le principe de base repose sur la possibilité d’effectuer un retour sur trace et d’effectuer un parcours en profondeur d’un arbre donné. Son article est librement accessible sur le site de l’Open Computing Facility de l’Université de Berkeley.

Au début, je voulais présenter une synthèse de son algorithme2 ainsi qu’une implémentation minimaliste. Mais entre temps je suis tombé sur SageMath qui en contient une version robuste et éprouvée. Ce code est développé et maintenu par Sébastien Labbé qui est, à l’heure de rédaction de ce billet, chargé de recherches au Laboratoire Bordelais de Recherche en Informatique.

SageMath, que j’ai découvert à l’occasion des mes recherches sur ce sujet, est un logiel libre dédié aux mathématiques. De ce que j’en comprends c’est un enrobage d’outils Python comme Numpy, Scipy ou Matplotlib afin de présenter une interface unifiée à l’utilisateur ainsi qu’une collection d’un certain nombre d’outils mathématiques (algèbre linéaire, polynômes, graphiques etc.).

Avant de passer à la présentation de la résolution du défi 28, j’aimerais illustrer ce que je pressentais lorsque j’évoquais le parcours du labyrinthe.

La page Wikipédia dédiée à la modélisation mathématique des labyrinthes propose plusieurs algorithmes générant des labyrinthes dit “parfaits” (chaque cellule du labyrinthe est reliée à toutes les autres de manière unique). Très vite apparaît la correspondance avec les graphes orientés acycliques. La notion d’acyclicité me paraît immédiate : on ne peut pas former de “boucles” car ça contredirait l’hypothèse d’unicité de chemin. Ce qui m’a plu, ce sont ces deux figures qui relient labyrinthe et graphe :

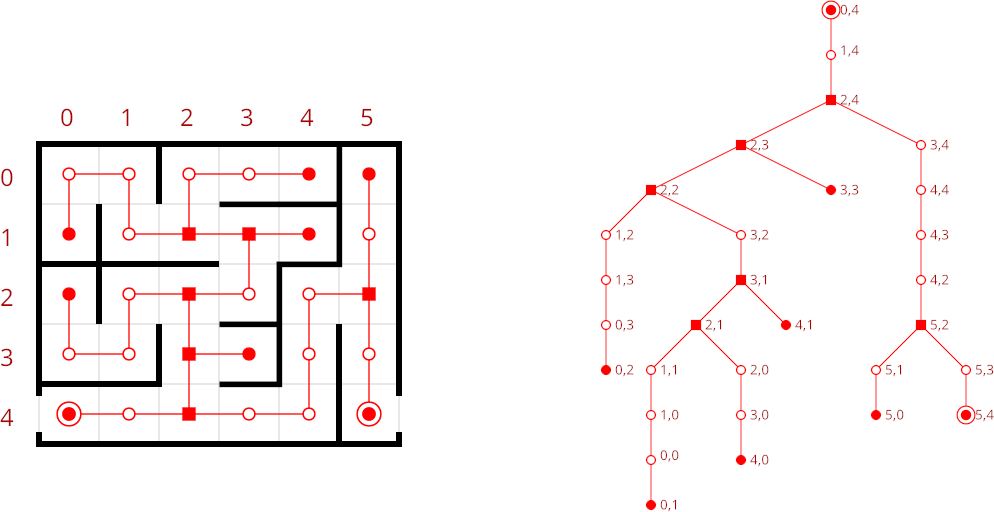
Equivalence avec un graphe

L’article de Knuth illustre le parcours des solutions (ici dans le cas particulier du pavage de Scott) par la figure suivante :

Parcours des solutions

On voit bien que la question est finalement similaire : sortir d’un labyrinthe et trouver un recouvrement exact reviennent tout deux à trouver une feuille de sortie en parcourant un arbre. Dans le cas du labyrinthe, cette feuille est généralement unique (il n’existe qu’une seule sortie) alors que dans le cas du pavage, il y a souvent plusieurs solutions.

Je vais maintenant tester le logiciel SageMath sur plusieurs cas particuliers afin de bien le prendre en main.

Premier cas : un seul polyomino qui rempli le cube $2\times 2 \times 2$

Tout d’abord, on s’attaque au problème trivial qui consiste à paver un cube $2\times 2 \times 2$ à l’aide d’un unique Polyomino qui est le cube lui-même. On s’attend à ne trouver qu’une seule solution (aux éventuelles symétries du Polyomino près).

from sage.combinat.tiling import TilingSolver, Polyomino
from sage.all_cmdline import *   # import sage library

L = [Polyomino([(0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0), (1,1,1)])];
T = TilingSolver(L, box=(2,2,2))

solution = next(T.solve())
G = sum([p.show3d(size=0.85) for p in solution], Graphics())
G.show(aspect_ratio=1, viewer='tachyon')

T.number_of_solutions()

Le solveur retourne $1$, ce qui est le résultat attendu. J’en déduis que l’implémentation SageMath de l’algorithme, lorsqu’elle construit sa matrice d’entrée, vérifie que les pièces tournées sont bien distinctes.

Deuxième cas : 8 monominos qui remplissent le cube $2\times 2 \times 2$

Cette fois-ci nous avons 8 petits cubes unitaires discernables (on va leur mettre à chacun une couleur différentes) qui doivent paver ce même cube $2\times 2 \times 2$. Les solutions sont là aussi triviales et on s’attend à en trouver autant qu’il n’y a de façons de permuter ces 8 petits cubes. Autrement dit, on devrait trouver $8! = 40 320$.

P1 = Polyomino([(0,0,0)], color='red')
P2 = Polyomino([(0,0,0)], color='green')
P3 = Polyomino([(0,0,0)], color='blue')
P4 = Polyomino([(0,0,0)], color='yellow')
P5 = Polyomino([(0,0,0)], color='magenta')
P6 = Polyomino([(0,0,0)], color='cyan')
P7 = Polyomino([(0,0,0)], color='black')
P8 = Polyomino([(0,0,0)], color='white')

L = [P1, P2, P3, P4, P5, P6, P7, P8];

T = TilingSolver(L, box=(2,2,2))
s = T.solve();


solution = next(s)


G = sum([p.show3d(size=0.85) for p in solution], Graphics())
G.show(aspect_ratio=1, viewer='tachyon')

T.number_of_solutions()
# 40 320 solutions, soit 8! --> OK les pièces sont discernables

Cette dernière instruction retourne bien $40 320$. Ci-dessous voici une de ces nombreuses solutions (telle que tracée par la fonction G.show()).

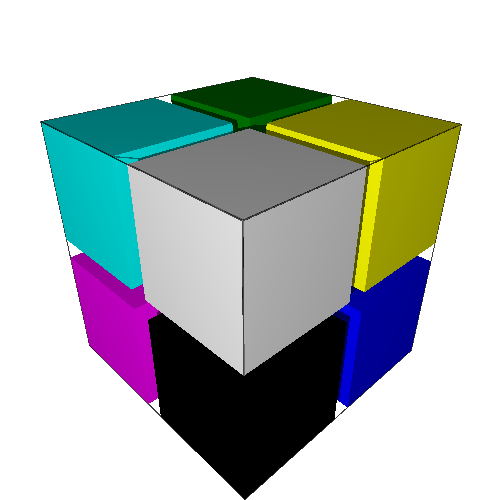
Huit petits cubes

Remarquons que nous aurions pu utiliser des monominos indiscernables à l’aide de l’argument reusable qu’il faut positionner sur True, auquel cas nous retrouvons bien une et une seule solution.

P = Polyomino([(0,0,0)], color='red')
T = TilingSolver([P], box=(2,2,2), reusable=True)
T.number_of_solutions()
# 1 seule solution...

Troisième cas : le cube Soma

On augmente un peu en difficulté et on s’attaque maintenant à l’exploration du cube Soma.

Il s’agit d’un casse-tête inventé dans les années 1930 par Piet Hein. Le nom fait référence au Soma du Meilleur des Mondes d’Aldous Huxley, une drogue addictive grâce à laquelle chaque élément de la société est heureux et ne revendique rien.

L’objectif du casse-tête est de paver un cube $3\times 3 \times 3$ à l’aide de sept polyominos prédéfinis.

Les sept polyominos du cube Soma

Le problème a été étudié par Martin Gardner et John Horton Conway et le livre “Winning Ways for your Mathematical Plays” en contient une analyse détaillée. Ce dernier livre, coécrit par Conway, est sorti en 1982 et se trouve aujourd’hui en occasion aux alentours de 90 € (dommage, il me branchait bien mais pas à ce prix là…). Il existe 240 façons distinctes de reconstituer le cube Soma à partir des sept polyominos de base. Arriverons-nous à retrouver ce résultat ?

P1 = Polyomino([(0,0,0), (0,0,1), (0,1,0)], color='red')
P2 = Polyomino([(0,0,0), (0,0,1), (0,1,0), (0,2,0)], color='red')
P3 = Polyomino([(0,0,0), (0,1,1), (0,1,0), (0,2,0)], color='red')
P4 = Polyomino([(0,0,1), (0,1,1), (0,1,0), (0,2,0)], color='red')
P5 = Polyomino([(0,0,0), (0,0,1), (1,0,1), (1,1,1)], color='red')
P6 = Polyomino([(0,0,0), (1,0,0), (1,0,1), (1,1,1)], color='red')
P7 = Polyomino([(0,0,0), (1,0,1), (1,0,0), (1,1,0)], color='red')


# G = P1.show3d()
# G.show(aspect_ratio=1, viewer='jmol')

T = TilingSolver([P1, P2, P3, P4, P5, P6, P7], box=(3,3,3))
T.number_of_solutions()

Cette fois-ci nous trouvons $11 520$ solutions ce qui est beaucoup trop ! Mais l’étude du pavage par huit petits cubes nous permet de comprendre que les symétries du cube ne sont pas prise en compte par l’algortihme ! On compte ainsi certaines solutions plusieurs fois !

Il nous faut donc diviser ce nombre par le nombre d’isométries du cube, qui est de $48$, et on retrouve bien le résultat attendu :

\[\frac{11 520}{48} = 240\]

En faisant cela, on fait l’hypothèse (vérifiée) que l’image de n’importe quelle solution du cube Soma par l’application d’une isométrie du cube est également une solution envisageable. Si les rotations ne posent généralement pas problème (en tournant le cube, on tourne également les pièces), ce n’est pas forcément le cas des symétries (qu’elles soient centrales ou planaires).

On ne peut par exemple pas exprimer une symétrie planaire comme composée de rotation 3D car la symétrie ne conserve pas l’orientation alors que la composée de rotation oui (une sombre histoire de signe du déterminant toute cette affaire là). Et lorsqu’on manipule les petites pièces avec nos gros doigts, on ne peut leur faire subir que des translations ou des rotations. On peut néanmoins s’en sortir si les pièces elles-mêmes possèdent certaines symétries de façon intrinsèque (quelque part, c’est lié à la chiralité des pièces).

Le fait que les cubes élémentaires constituant les polyominos sont indiscernables facilite grandement la non-chiralité des pièces. Mais ce n’est pas une condition suffisante, en témoigne cet exemple de pièce problématique que j’ai imaginé pour appuyer mon propos :

P = Polyomino([(0,0,0), (1,0,0), (0,1,0), (0,2,0), (0,0,1), (0,0,2), (0,0,3)])
G = P.show3d()
G.show(aspect_ratio=1, viewer='tachyon')

Une pièce problématique

On voit bien que l’image de cette pièce par une symétrie planaire ne serait pas, il me semble, accessible par une combinaison de rotations…

Peut-être que la clef serait de se demander si ces pièces sont orientées, c’est-à-dire qu’elles nous permettraient de définir un repère orienté de façon univoque. En cherchant du côté des mathématiques voire de la chimie on trouverait très probablement une réponse rigoureuse à cette question là.

Mais tout compte fait, le fait que tous les polyominos de Gagne ta Maman / ton Papa sont planaires me fait penser que nous ne rencontrerons jamais le moindre problème de chiralité en fait. Désolé si c’est un peu décousu, je rédige à peu près en même temps que je réflechis car j’ai envie de clôturer cet article et passer à autre chose ^^

Je m’éloigne finalement de mon propos premier, donc raison de plus de laisser là ces considérations et de passer au dernier cas, qui nous intéresse le plus.

Quatrième cas : le défi 28

Nous pouvons maintenant nous attaquer au fameux défi 28.

P1=Polyomino([(0,0,0)], color='red')
P2=Polyomino([(0,0,0), (0,1,0), (0,2,0), (1,0,0)], color='green')
P3=Polyomino([(0,0,0), (0,1,0), (0,2,0), (1,1,0)], color='blue')
P4=Polyomino([(0,0,0), (0,1,0), (1,1,0), (1,2,0)], color='yellow')
P5=Polyomino([(0,0,0), (0,1,0), (1,0,0), (1,1,0)], color='purple')
P6=Polyomino([(0,0,0), (0,1,0), (0,2,0), (1,0,0), (2,0,0)], color='black')
P7=Polyomino([(0,0,0), (1,0,0), (1,1,0), (1,2,0), (2,2,0)], color='blue')


L = [P1, P2, P3, P4, P5, P6, P7]

T = TilingSolver(L, box=(3,3,3))

T.number_of_solutions()

iterT = iter(T.solve());

for index, solution in enumerate(iterT):
     print('- Iteration ' +  str(index))
     G = sum([p.show3d(size=0.85) for p in solution], Graphics())
     G.show(aspect_ratio=1, viewer='tachyon', camera_position=cpx, 
frame=False)
     G.save_image('./figures/solution_' + str(index) + '.png')

Cette fois-ci nous trouvons $1 152$ solutions.

Il me semble que le miroir des pièces du défi sont toutes atteignables. En particulier j’avais une méfiance envers $Z_4$, $Z_5$ et (dans une moindre mesure) $L_4$. Mais je n’ai pas réussi à imaginer un cas de figure où une symétrie planaire conduirait à une solution impossible à réaliser. Je suppose que c’est OK.

En prenant en compte les isométries du cube, nous nous ramenons in fine à 24 solutions. Ces 24 solutions ne peuvent pas se déduire l’une de l’autre par le biais des symétries et rotations du cube.

Voici les 9 premières solutions retournées par le solveur de SageMath.

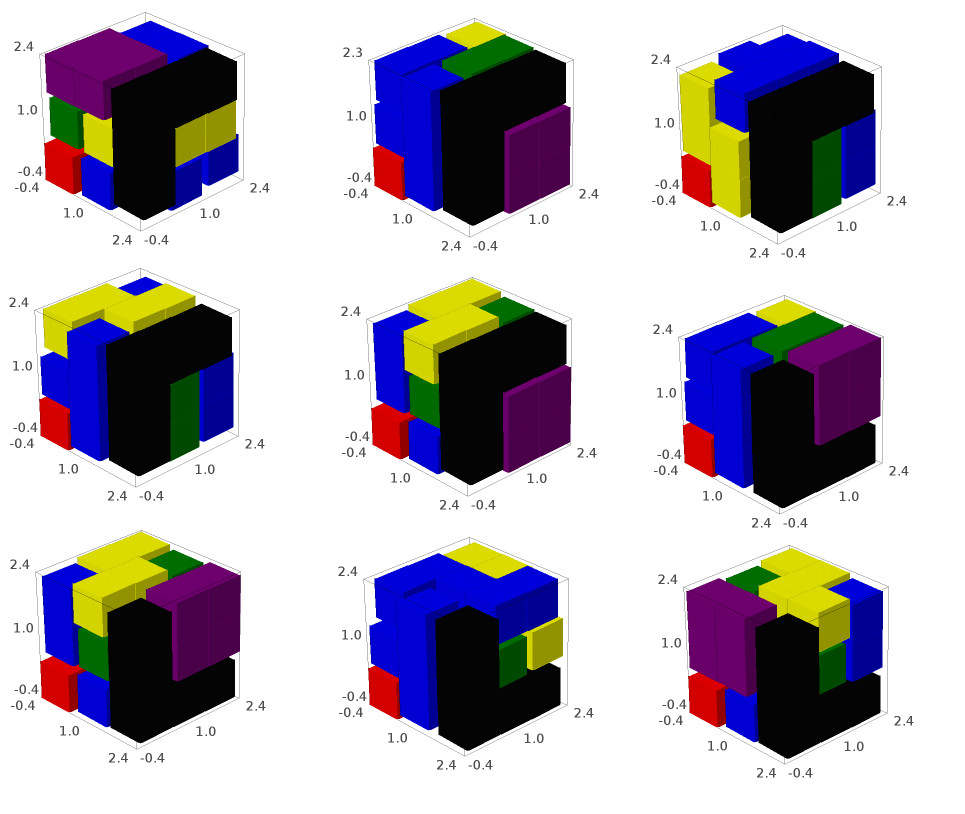
Neuf solutions du défi 28

Pour aller plus loin

Quelques idées que j’ai en tête :

  • ce défi 28 était-il particulièrement difficile ? Il faudrait tester les autres défis et calculer leur nombre de solutions
  • en mettant ce nombre de solutions en regard de certains paramètres (complexité des polyominos en terme de degré, nombre de polyominos, chiralité si cette dernière a un impact ?), des choses amusantes pourraient apparaître
  • on pourrait de même quantifier la difficulté du jeu standard (à savoir paver le rectangle)
  • on pourrait aussi étudier l’arbre des solutions : combien y-a-t’il de feuilles qui ne terminent pas ? Partant de cet arbre, nous pourrions générer le (gros) labyrinthe équivalent

Quelques liens utiles :

  1. dans le cas tridimensionnel, on préfère parfois le terme “polycubes” à “polyomino”. Dans la suite de ce billet, j’emploierai toujours “polyomino” pour simplifier. ↩

  2. la lecture de son article est très intéressante et instructive. Comme bien souvent en algorithmique, on se rend compte que la résolution élégante d’un problème passe en grande partie par la façon de modéliser les données du problème. Et l’algorithme proprement dit s’en déduit ensuite assez facilement. Je regrette juste qu’à un moment Knuth évoque la nomenclature de Golomb3 pour classifier les pentominos mais la référence associée pointe vers un livre assez rare (et donc cher)… Dommage… ↩

  3. ça m’a néanmoins permis de découvrir le mathématicien américain Solomon Wolf Golomb ainsi que ses règles éponymes ↩