Idées pour un logiciel de stéganographie audio
Bon, on va pas se mentir le blog est un peu en panne en ce moment…
Je dois avoir une quinzaine d’articles à moitié écrits, et à peu près autant de nouvelles idées qui trottent dans ma tête… juste pas le temps. Et lorsque j’arrive à dégager un peu de temps de ci de là, juste pas l’énergie…
Il y a un peu comme une inertie, le temps de mettre en place un environnement de travail sympa, de crayonner quelques idées, de développer un petit bout de code, de se plonger dans les éventuelles docs, de faire les recherches internet, de tester, bloquer, dépasser ou contourner etc.
Du coup, pour ne pas laisser le blog dans un état végétatif trop longtemps, je vais écrire ici un billet théorique qui n’incluera a priori aucun développement informatique. Par ailleurs, je vais limiter les recherches internet au minimum, ce que d’ailleurs je cherche toujours à faire afin de ne pas me laisser influencer par ce qui aurait déjà été fait ailleurs.
Il y a quelques mois, j’avais visionné la vidéo de Feldup concernant Cicada 3301. Il m’avait semblé qu’à un moment, mais je n’arrive plus à retrouver ce passage dans la vidéo, Feldup mentionne un message caché dans le signal audio d’un fichier mp3 fourni par Cicada 3301. Message qui serait inaudible mais qui se révélerait dans le spectrogramme du signal audio.
Ca ressemblait un peu à ça1 :

Du coup, je me suis mis à imaginer un petit algorithme qui chiffrerait et déchiffrerait un petit message de cette façon. On lui passerait en entrée un texte ainsi que le chemin vers un fichier audio et il insérerait automatiquement le premier dans le second. Il s’agit d’un cas particulier de stéganographie où le médium principal est du son et le médium secondaire du texte.
- Un premier modèle d’injection
- Réflexion sur un dimensionnement pertinent
- Extraction du signal
- Vers d’autres modèles
- En conclusion
Un premier modèle d’injection
Soit un alphabet pixelisé comme on peut le voir dans l’image ci-dessous

Une lettre peut être représentée par une matrice $(M_{i,j})$ de 5 lignes et 6 colonnes, avec $M_{i,j} = 1$ si le pixel en question fait partie de la lettre et $0$ sinon. Voici un exemple pour un possible codage de la lettre ‘A’. On voit que seuls les coefficients $M_{1,2}$, $M_{1,5}$, $M_{2,2}$, $M_{2,5}$, $M_{3,2}$, $M_{3,3}$, $M_{3,4}$, $M_{3,5}$, $M_{4,2}$, $M_{4,5}$, $M_{5,3}$ et $M_{5,4}$ sont non-nuls.
La numérotation des lignes ne suit pas la convention habituelle utilisée en mathématique : ici la première ligne est en bas. Ceci nous le verrons, facilitera la lecture des équations.

Si on souhaite insérer cette lettre à un temps arbitraire $t_0$ dans le morceau, alors on peut naïvement coder chaque pixel comme une sinusoïde pure qui serait jouée entre $t0 - \Delta t/2$ et $t0 + \Delta t/2$.
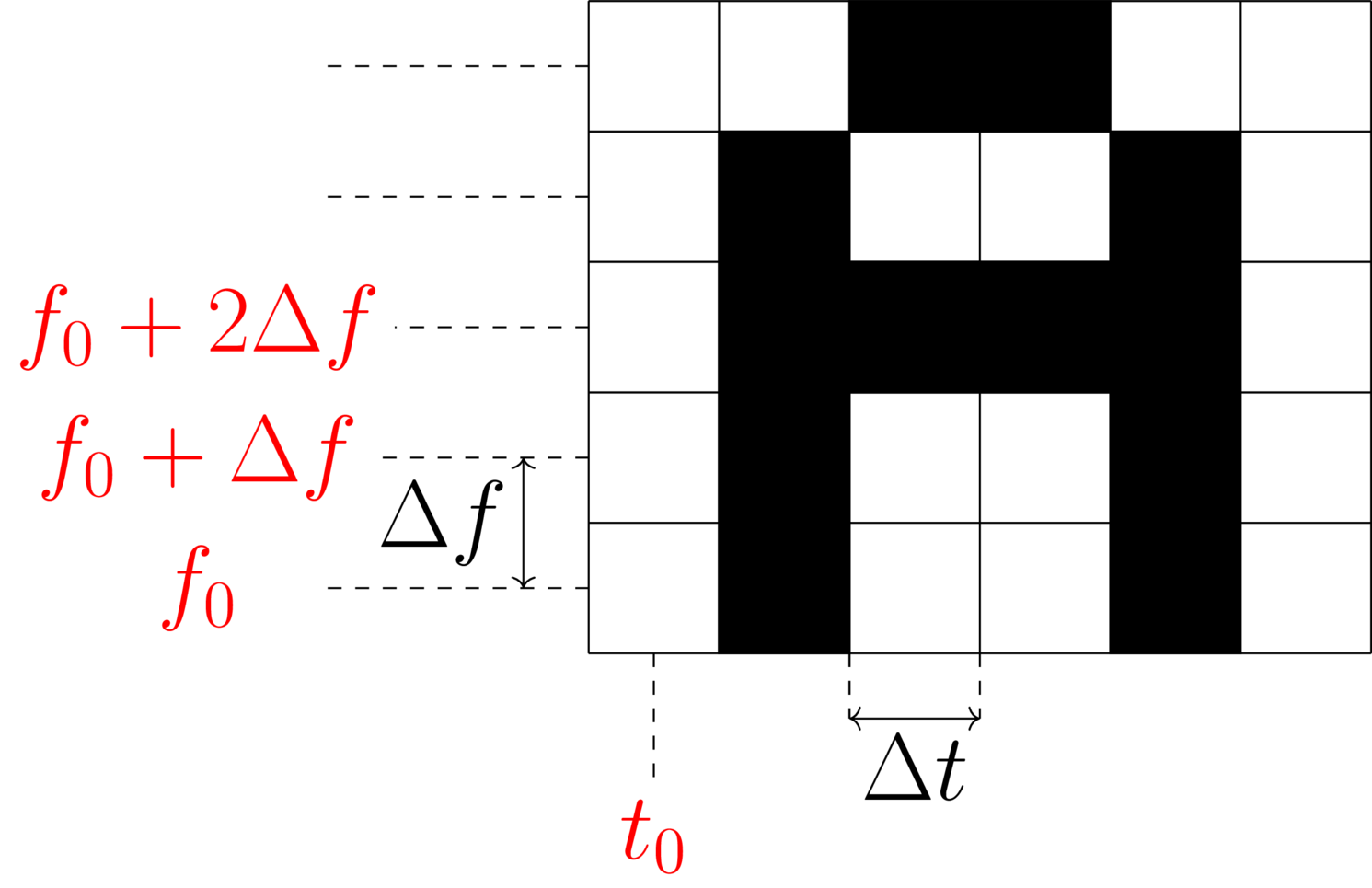
Ceci nous conduits à l’expression suivante du signal à injecter.
\[s(t) = K \times \sum_{i = 1}^{6} \sum_{j = 1}^{5} M_{i, j} \times cos\Big(2\pi (f+i \Delta f) t\Big) \times H\Big(t_0 + (j-1)\Delta t - \frac{\Delta t}{2}, t_0 + (j-1)\Delta t + \frac{\Delta t}{2}\Big)\]Le paramètre $K$ détermine l’amplitude du signal injecté, il devra être assez fort pour ne pas être noyé dans le bruit mais relativement faible pour ne pas être détecté à l’écoute. Il faudra probablement tester quelques valeurs. On peut aussi imaginer le calculer par rapport à l’énergie du mp3, voire même le définir à chaque pas de temps ET de fréquence, par rapport à la DSP du signal dans la portion temps/fréquence considérée.
La fonction $H(t_1, t_2)$ quant à elle est une fonction de fenêtrage arbitraire qui serait non-nulle le “temps du pixel”, par exemple une fenêtre de Hann ou de Hamming. L’idée est aussi de lisser un peu le signal pour minimiser les artefacts.
D’habitude, j’aime bien tester si la formule fonctionne bien mais là comme je le disais, aucune ligne de programmation. Je pense que ça doit marcher à peu près bien ce truc là.
La formule donnée ici représente une seule lettre mais il faut bien évidemment répéter le processus pour chacune des lettres du message à injecter en introduisant un délai incrémental de $6 \Delta t$. Toutes les lettres ne seront pas injectées à $t_0$ mais à $t_0$ puis $t_0 + 6 \Delta t$ puis $t_0 + 2 \times 6 \Delta t$, $t_0 + 3 \times 6 \Delta t$ etc.
Réflexion sur un dimensionnement pertinent
Alors bien sûr, il faut maintenant choisir correctement la fréquence initiale $f_0$, le pas en fréquence $\Delta f$ et la durée de chaque pixel $\Delta t$.
Préférons-nous un signal très resserré en fréquence ($\Delta f$ petit) auquel cas, l’auditeur pourrait percevoir un genre de sifflement ? Choisirons-nous plutôt d’étaler au maximum le spectre du signal injecté, auquel cas on augmente le risque que le signal injecté soit partiellement audible ?
La première considération concernant les fréquences est de comparer les bandes passantes de l’oreille humaine d’une part et de l’échantillonage du morceau (un CD de musique c’est du 44 kHz je crois). Naïevement, je me dis que la bande passante d’un enregistrement englobe plutôt généreusement la bande passante de l’oreille humaine. Du coup, il peut être judicieux de se placer un peu entre les deux.
Un petit schéma (rapide) de principe pour illustrer ça :
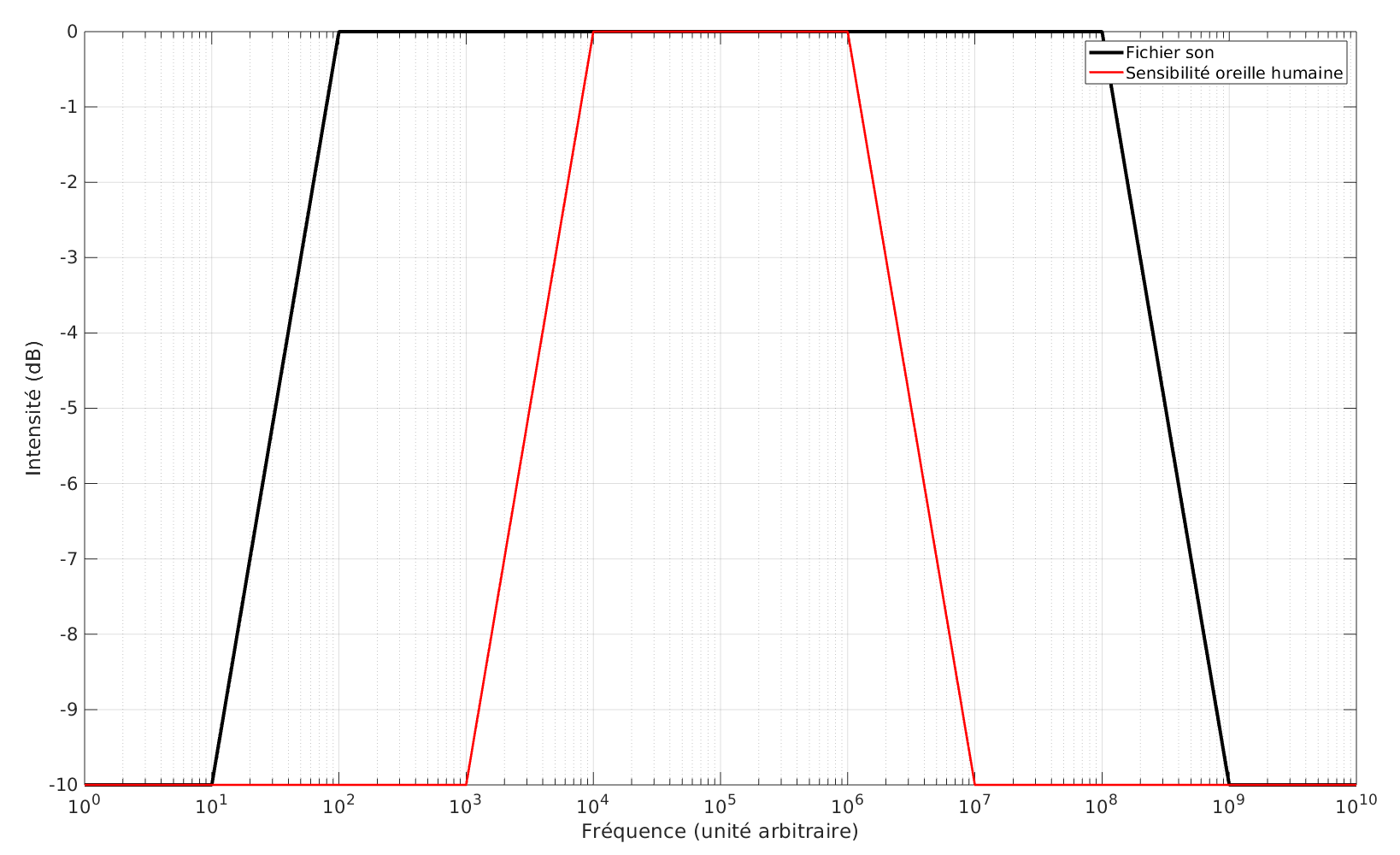
On aimerait a priori insérer nos lettres au-delà des fréquences de coupure de l’oreille humaine, donc soit dans les très basses fréquences, soit dans les très hautes fréquences.
Néanmoins, certains encodages audio (par exemple le mp3) vont justement réduire volontaire la dynamique du signal dans ces zones mortes afin de réduire la taille du fichier audio sans trop dégrader la qualité d’écoute. Dans ce processus, il est possible que notre signal texte soit affaibli voire corrompu. Au point de le rendre illisible ? Des essais seront nécessaires à ce stade.
Pour la durée des pixels, là encore des essais seront nécessaires. Avoir des temps longs réduit mécaniquement le nombre de caractères injectables dans le morceau mais nous offre la possibilité de diminuer le facteur d’amplitude $K$ (n’oublions pas que l’énergie de l’analyse temps-fréquence sera intégrée sur toute la longueur du pas de temps), ce qui rendra l’injection plus discrète.
Extraction du signal
Donc, nous avons quelques pistes pour développer l’injection d’un message texte dans un fichier audio, il nous faudrait maintenant parvenir à l’extraire.
La solution la plus simple est de faire une analyse temps-fréquence classique. Il faudrait idéalement que les paramètres de cette analyse (pas de temps, pas de fréquence, déphasage, recouvrement etc.) soient compatibles avec les paramètres de l’injection afin de limiter au maximum que le signal ne bave. Par exemple, si notre pas de temps est le double de celui choisi pour l’injection, nos pixels seront moyennés selon l’axe horizontal ce qui rendra la lecture difficile. De même, si on utilise le même pas de temps mais qu’on introduit un déphasage temporel, on aura là encore des signaux mélangés.
Si on ignore les paramètres du signal injecté, le mieux sera alors de tester différents jeux de paramètres jusqu’à avoir quelque chose de net. On peut aussi anticiper et minimiser ce problème en choisissant de long pas de temps et des fréquences très distinctes (donc $\Delta t$ et $\Delta f$ grands) afin d’avoir un message clair dans la majorité des cas.
On peut aussi penser que l’injection et l’extraction se feront avec exactement le même programme auquel cas, ces considérations n’ont plus lieu d’être : on sait exactement quoi regarder et à quel moment.
Une fois le spectogramme du signal obtenu, soit on considère que l’extraction est déterminée, soit on souhaite aller plus loin et convertir l’image en texte.
On pourrait alors filtrer le signal pour ne garder que la partie en fréquence correspondant au signal injecté (donc filtre passe-bande entre $f_0$ et $f_0 + 4 \Delta f$. Il suffirait de passer cette image à un logiciel de reconnaissance de caractères. Il y a très probablement des paquets python qui font ça très bien (encore une fois : pas de recherche internet !).
Ou alors, comme on connaît précisement l’alphabet utilisé (c’est-à-dire les matrices $M$ pour chaque lettre) et qu’on sait à quel moment elles ont été injectées, on peut développer nous-même notre propre logiciel de reconnaissance de caractères. La méthode la plus simple serait, pour chaque extraction de lettres, de choisir la lettre de notre alphabet qui minimise l’écart quadratique moyen (EQM). C’est très simple mais ça devrait bien marcher.
Le seul point ouvert que je vois ici est de savoir quand arrêter l’extraction du signal. Comment savoir si mon texte fait 5 ou 6 caractères ? A partir de quel moment j’arrête d’extraire des caractères et je commence à interpréter du bruit ? Peut-être mettre un seuil sur la valeur minimale attendue de l’EQM ou alors associer à chaque lettre extraite une probabilité liée à la valeur de l’EQM. Ou alors enfin, définir le pas en temps de telle façon que le texte s’étale sur la totalité du morceau. Encore une fois : des idées potentiellement à tester.
Vers d’autres modèles
Utiliser d’autres fonctions atomiques pour représenter les pixels
Rappelons ici la forme simplifiée du signal injecté pour un pixel d’une lettre :
\[s = K \times cos(t) \times H(t)\]En fréquence, la signature de ce signal temporel sera donc la convolution d’un cosinus et d’une fenêtre quelconque. Il y a peut-être plus malin comme “façon de remplir la case”. Encore une fois : à creuser, à tester.
Tirer partie des spécificités du médium
Par ailleurs, on suppose qu’il y a une bande en fréquence relativement peu bruitée mais cela va beaucoup changer selon qu’on écoute un discours ou un morceau de musique.
Dans ce dernier cas, j’imagine (à vérifier !) que la batterie d’un morceau pop-rock va créér périodiquement des genres de Dirac qui viendrait cracher dans toutes les fréquences. Ca aurait tendance à, ponctuellement, mettre tous les pixels à 1. Peut-être, peut-être pas. J’ignore aussi la durée de cette perturbation.
Mais on pourrait aussi envisager de tirer partie de cette caractéristique. Un signal ponctuel et très régulier, on peut considérer cela comme une horloge. Notre algorithme pourrait alors se synchroniser sur ce signal pour insérer une lettre et une seule juste après chaque coup de percussion. Peut-être (peut-être pas) que, de cette façon, le signal injecté serait complétement confondu avec la signature harmonique de la batterie. Tout est ici spéculatif. Mais ça serait une piste rigolote à explorer je pense. Il faudrait s’approcher assez près de la percussion pour passer inaperçu mais pas trop près non plus pour ne pas être perturbé par le son.
Une autre idée d’algorithme
Mais si on souhaite vraiment injecter discrètement un message caché dans un fichier audio, il y a des solutions à la fois beaucoup plus simples, robustes et discrètes.
Mettons de côté l’aspect encodage et considérons un signal audio pur (par exemple tel qu’il pourrait être stocké dans un fichier Wave). Ce signal est généralement stéréo, c’est-à-dire que nous disposons de deux séries temporelles $y_1$ et $y_2$ qui sont échantillonnées exactement de la même façon.
On pourrait alors envisager le codage suivant :
- si à un instant $t$, les signaux ont la même parité binaire (i.e. ils ont le même bit de poids faible) alors je génère un bit $1$
- sinon je génère un bit $0$
On va donc pouvoir injecter un signal très facilement en venant changer le bit de poids faible d’un des deux signaux selon le bit qu’on souhaite écrire. Avec une dynamique ordinaire de 16 bits, je doute que cette opération soit seulement détectable par une oreille humaine.
La quantité d’information injectable est par ailleurs beaucoup plus élevée qu’avec notre méthode un peu graphique présentée ici. Si on considère un encode ASCII basique, chaque lettre peut être codée sur 8 bits. Un morceau de musique de 2 minutes, échantillonné classiquement à 44 kHz, c’est déjà environ 5 millions de bits soit l’équivalent de 500 000 caractères ASCII, soit peu ou prou l’équivalent de Guerre et Paix de Tolstoï.
Bon après, un fichier audio Wave de deux minutes, on parle quand même d’un fichier de 20 mégaoctets donc normal qu’on puisse y stocker des choses.
Si on encode en mp3, il est très probable que ce signal haute fréquence (et plus précisement : la plus haute fréquence possible compte-tenu de l’échantillonage) soit complétement détruit. Je ne connais pas assez bien le mp3 pour continuer à creuser la question mais on pourrait envisager quelque chose de plus robuste mais moins efficace en capacité d’injection.
Par ailleurs, si les algorithmes présentés ici veulent dépasser la stéganographie “récréative” mais ambitionnent d’être des méthodes de chiffrements, alors ils ne valent pas tripettes. Déjà ils sont très simples et surtout ils ne respectent pas le principe de Kerckhoffs : quiconque connaît l’algorithme sera en mesure de déchiffrer n’importe quel message.
En conclusion
- Les différents points soulevés n’ont pas vraiment été creusés
- Je me doute que ce qui est présenté ici, c’est du déjà vu et revu ailleurs2
- Les graphiques pour illustrer mon propos ont été fait à l’arrache3
- Je n’ai absolument rien codé pour tester la validité de ce que je raconte ici4
Néanmoins…
… je suis bien content d’avoir un peu repris l’écriture de ce blog :)
-
c’est la miniature d’une vidéo youTube d’un certain “zips . exe”. Du coup j’ai screené vite faire le contenu de la vidéo après l’écriture de l’article, il indique un méthode pour notre algo qui utilise Audacity. J’ai pas tout regardé mais il me semble que le signal injecté est clairement audible (le genre de sifflement que j’anticipais justement). ↩
-
mais encore une fois, je n’aime pas être influencé ↩
-
mais c’est du LaTeX/Tikz donc ça reste globalement beau. J’aurais aimé réduire la taille du texte sur le schéma de la lettre A (ça fait un peu trop gros). Et pour la courbe de bande passante (faite en Matlab), cette fois-ci c’est la taille de la légende qui me paraît un peu petite. Mais bref : assumons le côté expéditif (et expédié) de la chose ! ↩
-
mais je sais que c’est globalement ok, faut pas déconner non plus ↩