C’était peut-être un peu tôt mais finalement on s’est beaucoup amusé. Avec Marie nous avons passé quelques après-midi à réaliser des roues de César. Je rends compte de tout cela dans ce billet de blog.

La roue de César

Le chiffre de César est un cas particulier de chiffrement par substitution où nous décalons chaque lettre de l’alphabet d’une certaine valeur (positive ou négative). Cette valeur de décalage constitue en quelque sorte la clef du chiffrement.

Le code est très simple et peut très facilement se casser. Soit par attaque par force brute (il n’y a que 26 clefs pour l’alphabet latin) soit par analyse fréquentielle.

Un algorithme un peu plus évolué serait le chiffre de Vigenère qui utilise des clefs de taille arbitraire. C’est un peu plus robuste mais ça peut se casser (notamment pour lorsque le message à coder est grand devant la longueur de la clef), par exemple via le test de Kasiski.

Mais laissons cela de côté pour le moment, l’idée était de montrer à ma fille de 5 ans et demi qu’il était possible de coder des messages secrets que nous serions les seuls, elle et moi, à pouvoir lire.

Ci-dessous, un exemple de roue de César, générée avec un code p5.js.

Et voici la première roue que nous avons construite, Marie et moi !

Roue de César maison

Par exemple, le message “BONJOUR” avec un décalage de +1 donnera “CPOKPVS”. Un décalage de +1 transformera chaque A en B, chaque B en C etc… Jusqu’au Z qui, c’est circulaire, sera transformé en A.

Pour décoder, il suffira d’appliquer un décalage de -1 au message chiffré. Le premier C du message sera donc transformé en B et ainsi de suite, jusqu’à reconstituer le message initial : “BONJOUR”.

On peut bien entendu utiliser n’importe quelle valeur de décalage.

Pour nous aider dans ces transformations, on fait tourner la roue extérieure d’un certain nombre de secteurs dans le sens horaire, si la clef est positive, ou dans le sens anti-horaire si la clef est négative. La table de substitution s’établit alors en faisant correspondre les lettres de l’anneau extérieur avec celles de l’anneau intérieur. Partir de l’extérieur vers l’intérieur, c’est chiffrer. Partir de l’intérieur vers l’extérieur, c’est déchiffrer1.

Pour faciliter la communication de la clef de chiffrement avec Marie, j’ai plutôt transmis un alignement de la forme $\frac{A}{B}$ qui signifie que la roue doit être dans une position telle que la lettre A doit être au-dessus de la lettre B. En pratique, ça fonctionne bien.

Notons le cas particulier du ROT-13 qui est un codage de César avec un décalage de $26/2 = 13$ cases. Celà revient à effectuer un demi-tour sur la roue supérieure, comme illustré ci-dessous. Cette fois-ci la roue (statique) a été générée avec un code TikZ/LaTeX que je fournis en fin d’article.

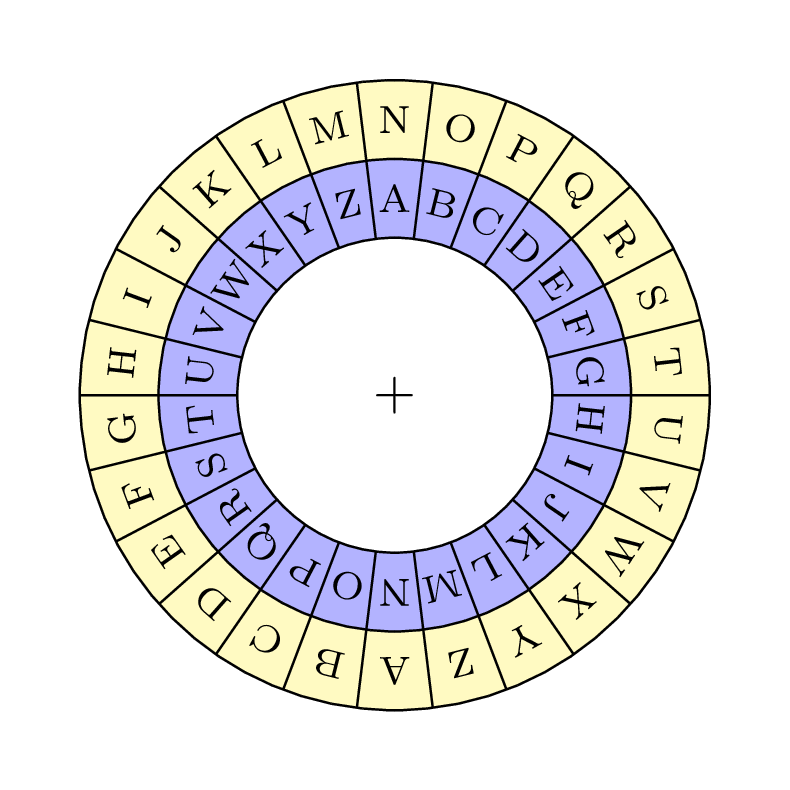
Configuration de la roue en ROT-13

Dans cette configuration, on code et on décode exactement de la même façon. Autrement dit, coder deux fois de suite un message renverra le message en clair. C’est l’unique configuration symétrique de la roue2.

Matériel

  • Papier à dessin blanc Canson A4, $224\,g/m^2$
  • Attaches parisiennes Exacompta, longueur $30\,mm$
  • Compas
  • Règle
  • Ciseaux
  • Feutres et crayons de couleurs

Construction

  1. On commence par tracer le plus grand cercle possible $C_1$ dans la feuille A4, soit un cercle de rayon $r_1 = 10\,cm$ environ
  2. On trace ensuite un cercle concentrique $C_2$ de plus petit rayon, par exemple $r_2 = 7 cm$ : l’anneau délimité par les deux cercles contiendra la première séquence des lettres (en jaune sur le schéma ci-dessus)
  3. Sur la même feuille s’il y a la place ou bien sur une autre feuille, tracer un troisième cercle $C_3$ de rayon $r_3 = r_2$ et extérieur à $C_1$
  4. Enfin tracer un quatrième et dernier cercle $C_4$, concentrique avec $C_3$ et de rayon $r_4 < r_3$ (on pourra choisir $r_4$ tel que $r_3 - r_4 = r_1 - r_2$) : de la même façon que précédemment, l’anneau délimité par $C_3$ et $C_4$ contiendra la seconde séquence de lettres (en bleu sur le schéma ci-dessus)
  5. On prend bien soin de matérialiser le centre des cercles par une petite croix (c’est ici qu’on placera l’attache parisienne)
  6. L’étape cruciale est ensuite de diviser ces cercles en 26 secteurs de même ouverture angulaire. Nous rendons compte de cela dans le reste de l’article
  7. Découper ensuite les deux parties de la roue
  8. Assembler ces disques à l’aide de l’attache parisienne
  9. Ecrire les lettres sur les roues et colorier comme on veut

Construction des polygones réguliers

Diviser un cercle en $N=26$ secteurs de même ouverture angulaire, cela revient à placer $N$ points équirépartis sur le cercle c’est-à-dire à construire un polygone régulier à 26 côtés.

Le problème est loin d’être trivial et a été totalement résolu en 1837.

Le théorème de Gauss-Wantzel donne effectivement les conditions nécessaires et suffisantes pour qu’un tel polygone régulier soit constructible uniquement à la règle (non graduée) et au compas.

Le polygone régulier de degré $N$ est constructible si et seulement si $N$ peut s’écrire de la façon suivante :

\[N = 2^p\cdot F_n\]

Avec $p$ un entier (potentiellement nul) et $F_n$ un nombre de Fermat premier.

Les nombres de Fermat sont de la forme suivante :

\[F_n = 2^{2^n} + 1\]

Voici les six premiers éléments de cette suite.

$n$ $F_n$
0 3
1 5
2 17
3 257
4 65 537
5 4 294 967 297

La suite, on le voit, croît extrémement vite. Elle est référencée sous l’identifiant A000215 sur l’encyclopédie en ligne des suites entières (OEIS).

Fermat pensait initialement que tous les nombres $F_n$ étaient premiers et c’est effectivement le cas des cinq premiers termes.

En revanche $F_5$ est composé puisque :

\[F_5 = 2^{2^5} + 1 = 2^{32} + 1 = 4294967297 = 641 \times 6 700 417\]

A l’heure actuelle, on ignore s’il existe d’autres nombres de Fermat premiers mais il est conjecturé qu’il n’y en a pas d’autres. La suite A019434 de l’OEIS liste les nombres de Fermat premiers connus.

Gauss tentant de résoudre la question de la constructabilité des polygones réguliers “Mais qu’est-ce que c’est que tout ce bazar par terre ? Ne me dis pas que tu as encore essayé de démontrer la constructabilité des polygones réguliers ?” (Statue de Carl Friedrich Gauss photographiée par l’auteur lors de son passage à Göttingen)

Le plus petit polygone régulier qui ne soit pas constructible est par exemple l’heptagone.

De façon générale, la suite A004169 de l’OEIS liste les polygones réguliers qui NE peuvent PAS être construits à la règle et au compas. De façon amusante, la suite A003401 elle, liste les polygones réguliers qui peuvent être construits à la règle et au compas.

Voici la liste des nombres de côtés des premiers polygones constructibles : 1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30, etc.

On le voit, le nombre 26 n’apparaît dans la séquence A004169, nous savons donc qu’il est impossible de diviser notre roue en 26 secteurs. Il nous faut donc passer par une méthode approchée.

Au passage, le plus grand polygone régulier de moins de 26 côtés est l’icosikaitétragone (également appelé tétraicosagone) qui comporte 24 côtés. Je n’ai pas trouvé le nombre d’étapes nécessaires pour le construire mais je pense que c’est fastidieux.

Méthode approchée pour diviser le cercle en 26 cadrans

Je vois deux méthodes :

  1. Utiliser un rapporteur et rapporter 25 fois l’ouverture angulaire $\theta = 2\pi/26 \approx 0.24\,\textrm{rad} = 13.84^\circ$
  2. Calculer la longueur de la corde de chaque secteur et la rapporter avec un compas

N’ayant pas de rapporteur sous la main, c’est cette dernière solution que j’ai gardée.

Nous avons que, dans un cercle de rayon $r$, une corde interceptant un angle au centre $\theta$ aura une longueur $L$ donnée par la relation suivante :

\[L = 2r\sin \left( \frac{\theta}{2} \right)\]

La longueur $L$ et l’angle $\theta$ sont représentés dans le schéma ci-dessous dans le cas de l’octogone régulier convexe.

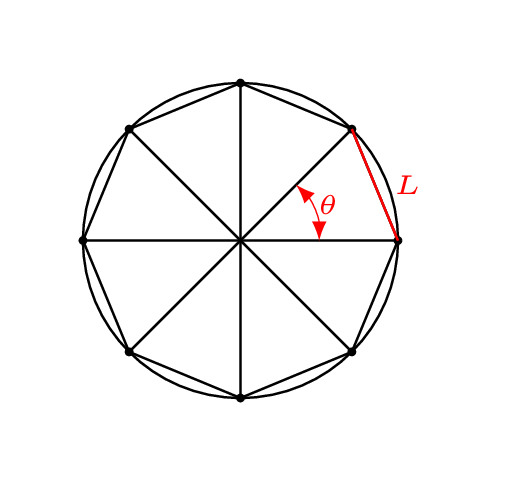
Longueur de corde d'un octogone

Avec notre grand cercle de 10 cm de rayon, nous obtenons ainsi une longueur de corde de $L \approx 2.41$ cm.

Résultat

Voici ce qu’on obtient au final :

Roue de César maison

Le résultat est très propre (les secteurs sont bien tous de la même longueur) et je trouve que Marie l’a très bien coloriée : c’est une jolie roue, agréable à regarder et à manipuler.

Marie s’est occupée d’écrire les lettres de l’anneau supérieur et je me suis chargé de celles de l’anneau inférieur.

Nous avons joué pas mal de temps avec cette roue. je m’amusais à passer à Marie des messages codés avec une clef (un décalage). Marie déchiffrait ensuite le message. Nous avons par la suite envoyé des messages codés à Maman et Mémé.

Forts de cette première expérience, nous avons réalisé d’autres roues avec des diamètres et des alphabets sensiblement différents mais cette fois-ci l’erreur cumulée sur les tailles des secteurs était beaucoup plus substancielle.

Avons-nous bâclé le travail suite à cette première réussite ? Nous sommes-nous endormi sur nos lauriers ? Ou bien au contraire, nous sommes-nous placés sans le savoir dans une situation plus difficile à réaliser ? C’est l’enjeu de la section suivante.

Un modèle de propagation d’erreur

On le devine : une petite erreur sur l’ouverture angulaire de notre compas pour reporter 26 fois la mesure de $L$ va se traduire, pour le dernier secteur, par une erreur non négligeable.

Une règle vue de près

On peut supposer grossièrement que notre modèle d’erreur sera un arrondi à la première décimale. Ainsi une longueur de 2.41 cm sera de seulement 2.4 cm alors qu’une longueur de 2.47 cm sera elle de 2.5 cm.

Mathématiquement, on écrit :

\[\widetilde{L} = \frac{\left\lfloor 10 \cdot L + 0.5 \right\rfloor}{10}\]

Voici l’allure de l’erreur absolue3 $\Delta L = L - \widetilde{L}$ pour $L$ variant entre $2$ et $3$ :

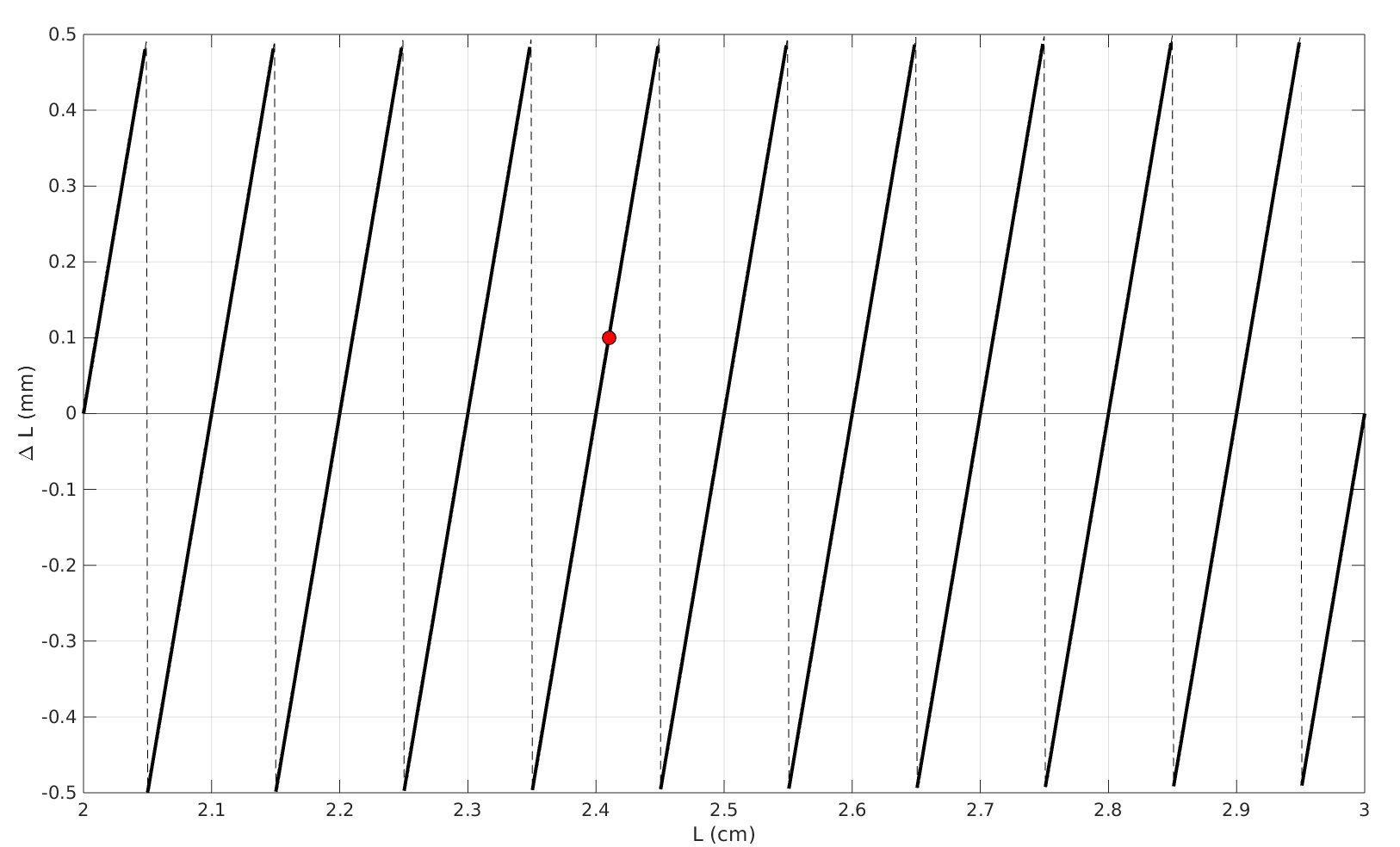
Erreur absolue sur la mesure du compas

On constate que l’erreur est nulle lorsque $L$ tombe juste sur la règle (par exemple lorsqu’on cherche à reporter au compas une distance de 2.0 cm, 2.1 cm, 2.2 cm etc.). Elle est maximale (avec une discontinuité) lorsqu’on s’approche du milieu entre deux graduations (donc par exemple 2.05 cm, 2.15 cm, 2.25 cm etc.). Bien entendu nous ne sommes pas des robots et la réalité ne sera pas aussi “tranchée” que ce modèle. Mais enfin, nous pouvons de cette façon dimensionner grossiérement l’ordre de grandeur attendu sur l’erreur lorsque (sacrilège !) on utilise un compas avec une règle graduée.

Le point rouge sur la figure correspond au cas particulier de notre roue de 10 cm. Rappelons-nous que, souhaitant diviser ce cercle en 26 secteurs identiques, nous devions reporter des cordes de 2.41 cm. Selon notre modèle d’erreur, nous reporterons plus vraisemblablement des cordes de 2.4 cm, soit une erreur absolue de 0.1 mm. Cela semble peu.

Néanmoins, les erreurs vont se cumuler de secteurs en secteurs de sorte que le dernier secteurs sera trop petit d’exactement 2.6 mm. Rapporté à la longueur souhaitée de la corde (2.41 cm), cela représente tout de même une erreur relative de 10% ce qui n’est pas négligeable !

Nous le voyons, nous devons raisonner sur l’erreur absolue du dernier secteur $\Delta$ qui s’écrit :

\[\Delta = n \cdot \Delta L = n \cdot (L - \widetilde{L})\]

Ce qui peut se mettre sous la forme d’une erreur relative $\delta$ :

\[\delta = \frac{\Delta}{L}\cdot 100 = \frac{n \cdot \Delta L}{L}\cdot 100\]

Voici dans la figure ci-dessous et en toute généralité l’erreur relative attendue pour différents couples de rayon / nombre de secteurs. Nous voyons trois phénomènes remarquables :

  • Les espèces d’oscillations, qui dessinent des petits drapeaux français, proviennent directement de notre modèle d’erreur qui oscille avec $L$ (rappelez-vous la courbe ci-dessus où $\Delta L$ était tracé en fonction de $L$)
  • Plus le rayon est grand et plus $L$ sera grand et donc l’erreur d’arrondi tendra à être négligeable devant $L$, ce qui conduit à diminuer l’erreur relative finale
  • Plus le nombre de secteur est grand et plus l’écart absolu final $\Delta$ sera potentiellement important. Ca semble à première vue linéaire mais n’oublions pas, qu’à $r$ fixé, la valeur de $L$ (et donc de $\widetilde{L}$) varie également avec $n$.

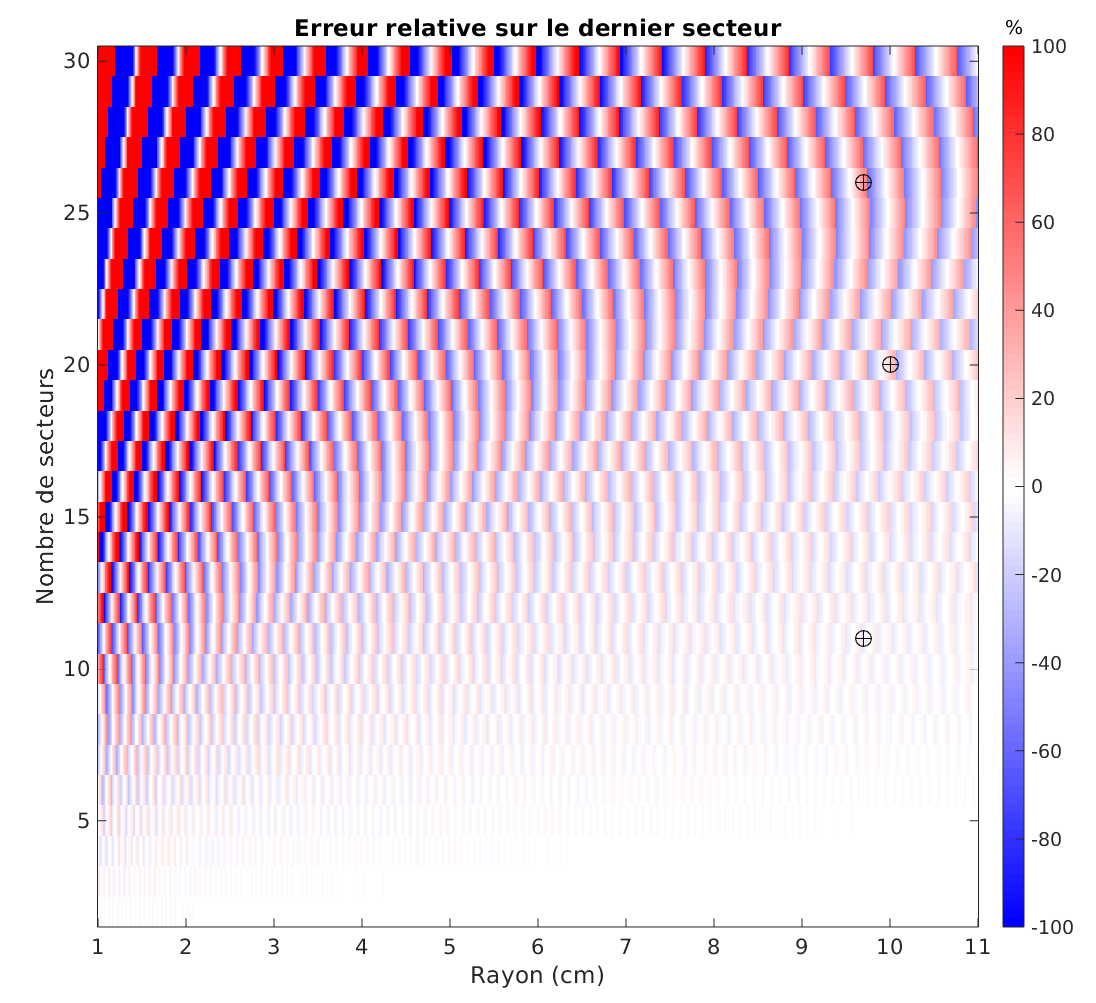
Un modèle de propagation d'erreurs

Les trois petits cercles indiquent les paramètres utilisés pour les trois roues que nous avons créées. La première roue qui, paradoxalement, est à la fois la délicate à réaliser (erreur finale élevée) et pourtant la plus propre dans sa réalisation, apparaît tout en haut (26 secteurs et, je crois, 9.7 cm de rayon).

Au final, j’en conclus que j’ai probablement bâclé le travail pour les deux roues suivantes, qui auraient du être plus simple à réaliser.

Notons au passage que j’ai supposé que l’écartement du compas demeurait fixe tout au long de la construction : la seule erreur provenant ainsi de l’écartement initial sur la règle graduée. Ce n’est peut-être pas le cas et, un faux mouvement à un moment pourrait tout à fait expliquer la moindre qualité des deux autres roues.

Remarquons enfin que si j’avais eu un rapporteur, alors le modèle d’erreur aurait été très différent : les erreurs ne se cumulent plus forcément mais il y aurait eu une certaine dispersion autour de la valeur moyenne. Le résultat aurait peut-être été de meilleur qualité. J’ignore à quoi ça ressemble de rapporter un angle de $13.84$ degrés, c’est presque $14$ degrés. Et le rayon du cercle n’intervient plus. La taille du rapporteur doit également jouer un rôle dans la précision de la construction.

Utilisations ludiques de la roue de César

Au-delà de la roue de César classique, Marie a voulu réaliser deux autres roues basées sur des alphabets complétement différents.

La roue des nombres

Dans cette roue des nombres comportant 11 secteurs, Marie a placé les nombres de $0$ à $10$.

Nous n’avons pas vraiment joué avec cette roue ci, j’ignore quelle pourrait en être son utilisation.

On pourrait envisager un codage en base onze et introduire un alphabet codé sur deux symboles successifs (soit $11\times 11 = 121$ lettres). Mais ça serait quand même un peu fastidieux.

La roue des nombres

La roue des formes

On s’est en revanche beaucoup plus amusés avec la roue des formes pour laquelle elle a spontanément proposé une règle du jeu que je trouve très amusante.

Cette roue comporte 20 secteurs contenant chacun un petit dessin (un triange, un coeur, un nuage etc.). Marie a dessiné les formes de l’anneau supérieur et je me suis contenté de les recopier du mieux que je pouvais dans l’anneau inférieur.

L’idée est la suivante : nous mettons en relation deux formes et il s’agit de dessiner ce qu’il pourrait se passer si nous mélangions ces deux formes.

Par exemple un coeur et un nuage nous inciteraient à dessiner un nuage en forme de coeur.

J’ai trouvé cette idée très originale et amusante.

La roue des formes

Code TikZ/LaTeX pour générer des roues de César

Je termine par le code TikZ/LaTeX permettant de générer une roue de César sur l’alphabet latin (donc 26 lettres). Compilé en l’état, ce code va générer un fichier PDF qu’on pourra ensuite imprimer et découper.

Vous pouvez l’adapter à vos besoin comme vous le souhaitez. Prenez garde à mettre des valeurs de rayon de cercle “réalistes”. Ici j’ai choisi des valeurs qui remplissent bien la feuille A4.

On compile ensuite le code. Chez moi ce sera par exemple :

$ pdflatex cesar.tex -o cesar.pdf

% Roue de César en Tikz/LaTeX
% Auteur 	: DonutMan
% Date 		: 2023-02-29
% License 	: GNU GPLv3

% Utilisation
% 1. Vous pouvez mettre à jour les paramètres des rayons des 4 cercles via les varibles ra, rb et rc
% 2. Vous pouvez également changer la couleur des roues (et ajouter d'autres options éventuelles comme l'épaisseur
%    ou la couleur du tracé des cercles) via les définitions de style TikZ outterring et innerring
% 3. Compilez classiquement ce document, par exemple chez moi ce sera
%      $ pdflatex cesar.tex -o cesar.pdf
% 4. Imprimez, découpez et assemblez (il n'est pas nécessaire d'imprimer la première page)

% Notes
% - pas de vérifications si les valeurs des rayons sont réalistes, vous êtes grands
% - le programme fonctionne uniquement avec 26 secteurs (ce serait fastidieux de mettre ça en variable)
%   et les lettres sont celles de l'alphabet latin classique, mais il est possible de l'adapter à votre besoin !
%   Vous pouvez également supprimer l'écriture des lettres en commentant les lignes qui contiennent "\scriptsize \letter"



\documentclass{article}

\usepackage [francais]{babel}
\usepackage [T1]{fontenc}
\usepackage [utf8]{inputenc}
\usepackage[a4paper, left=10mm, right=10mm]{geometry}
\usepackage{tikz}
\pagestyle{empty}

\title{Roue de César}
\author{Donut Man}
\date{\today}


% Some parameters that can be adjusted :

\providecommand{\ra}{8} % Circle radius for circle C1
\providecommand{\rb}{7}  % Circle radius for circles C2 and C3
\providecommand{\rc}{6}  % Circle radius for circle C4

\tikzstyle{outterring}=[fill=yellow!30] % Tikz style of outter ring
\tikzstyle{innerring}=[fill=blue!30]   % Tikz style of inner ring

% End of parameters


\pgfmathsetmacro{\rab}{(\ra+\rb)/2} % Radius location of letters of the external ring
\pgfmathsetmacro{\rbc}{(\rb+\rc)/2} % Radius location of letters of the internal ring


\begin{document}

\maketitle
\thispagestyle{empty}

Instructions :
\begin{enumerate}
\item Découpez les deux roues des pages suivantes
\item Percez un petit trou au niveau des centres des deux roues
\item Assemblez les deux roues à l'aide d'une attache parisienne
\item Profitez :)
\end{enumerate}

\vspace{1.5cm}

% Roue totale (fixe en taille)
\begin{center}
\begin{tikzpicture}

\draw[outterring] (0,0) circle (6);
\draw[innerring] (0,0) circle (5);
\draw[fill=white] (0,0) circle (4) node{$+$};



\foreach \letter [count=\k from 0] in {Z,Y,...,A} {

	% Some parameters computation
	\pgfmathsetmacro{\thetacesar}{360*(\k+0.5)/26+90} % Angle of each sector
	\pgfmathsetmacro{\thetacentre}{360*(\k+1)/26+90} % Center angle of each sector
	\pgfmathsetmacro{\rotationangle}{-90+\thetacentre} % Angle rotation (in degree) for the text
	
	
	\draw (\thetacesar:6) -- (\thetacesar:4);
	\draw (\thetacentre:5.5) node[rotate=\rotationangle]{\scriptsize \letter};
	\draw (\thetacentre:4.5) node[rotate=\rotationangle]{\scriptsize \letter};
}

\end{tikzpicture}
\end{center}





% Roue extérieure
\clearpage
\vspace*{\stretch{1}}
\begin{center}
\begin{tikzpicture}

\draw[outterring] (0,0) circle (\ra);
\draw[fill=white] (0,0) circle (\rb) node{$+$};



\foreach \letter [count=\k from 0] in {Z,Y,...,A} {

	% Some parameters computation
	\pgfmathsetmacro{\thetacesar}{360*(\k+0.5)/26+90} % Angle of each sector
	\pgfmathsetmacro{\thetacentre}{360*(\k+1)/26+90} % Center angle of each sector
	\pgfmathsetmacro{\rotationangle}{-90+\thetacentre} % Angle rotation (in degree) for the text
	
	
	\draw (\thetacesar:\ra) -- (\thetacesar:\rb);
	\draw (\thetacentre:\rab) node[rotate=\rotationangle]{\scriptsize \letter};
}

\end{tikzpicture}
\end{center}
\vspace*{\stretch{1}}




% Roue intérieure
\clearpage
\vspace*{\stretch{1}}
\begin{center}
\begin{tikzpicture}

\draw[innerring] (0,0) circle (\rb);
\draw[fill=white] (0,0) circle (\rc) node{$+$};



\foreach \letter [count=\k from 0] in {Z,Y,...,A} {

	% Some parameters computation
	\pgfmathsetmacro{\thetacesar}{360*(\k+0.5)/26+90} % Angle of each sector
	\pgfmathsetmacro{\thetacentre}{360*(\k+1)/26+90} % Center angle of each sector
	\pgfmathsetmacro{\rotationangle}{-90+\thetacentre} % Angle rotation (in degree) for the text
	
	
	\draw (\thetacesar:\rb) -- (\thetacesar:\rc);
	\draw (\thetacentre:\rbc) node[rotate=\rotationangle]{\scriptsize \letter};
}

\end{tikzpicture}
\end{center}
\vspace*{\stretch{1}}


\end{document}

  1. De même que pour le sens de rotation du disque, le distingo chiffrer/déchiffer relève d’une convention arbitraire, nous aurions pu tout aussi bien chiffrer en partant de l’intérieur vers l’extérieur ou bien convenir qu’un décalage positif consiste à tourner le disque dans un sens anti-horaire. Le tout est de se mettre d’accord sur un protocole. ↩

  2. Ceci sans compter bien entendu la transformation Identité (A$\to$A, B$\to$B, …, Z$\to$Z) qui est elle aussi symétrique. ↩

  3. Bon OK, erreur de signe classique, j’aurais du prendre $\Delta L = \widetilde{L} -L$ de sorte que si $\widetilde{L} > L$ alors $\Delta L > 0$, mais enfin la flemme de refaire les graphiques. Et ça ne change rien aux conclusions développées ici. ↩