Castagnette et Guimbarde
Ca fait quelques temps que j’ai remarqué un phénomène curieux chez moi : lorsque je tape des mains dans certains endroits de la maison, j’entends un curieux écho que je n’ai jamais réussi à clairement identifier. Voyons si quelques éléments de traitement du signal peuvent nous venir en aide ici.
- Description du phénomène
- Analyse temporelle
- Analyse temps-fréquence
- Identification de la source du bruit
- Analogie avec la guimbarde
- Analogie avec la règle en plastique
- Vers un modèle de bruit
- Pistes pour la suite ?
- Conclusion
- Sources
Description du phénomène
Afin d’avoir le son le plus caractéristique possible, j’ai utilisé un générateur de dirac acoustique : la castagnette. Pardonnez le style un peu enfantin de l’instrument, je l’ai emprunté à ma fille Alice qui a 1 an.

Je me suis promené un peu dans toutes les pièces : le son étrange est particulièrement fort dans les chambres et dans une moitié du salon; il est inaudible partout ailleurs.
Voici un exemple du phénomène acoustique, capturé par l’enregistreur de mon smartphone (signal échantillonné à 44 100 Hz). On entend au tout début le claquement sec de la castagnette puis dans la foulée une vibration modulée qui évoque un peu la guimbarde ou le son d’une règle en plastique coincée sur un coin de table et qu’on ferait osciller. La durée du phénomène est d’environ 500 ms.
Analyse temporelle
Voici le tracé temporel du signal sonore que vous venez d’entendre. Nous reconnaissons aisément le signal de la castagnette (un dirac ici centré en 0) et nous observons un retour assez riche qui s’estompe au bout de 500 ms environ.
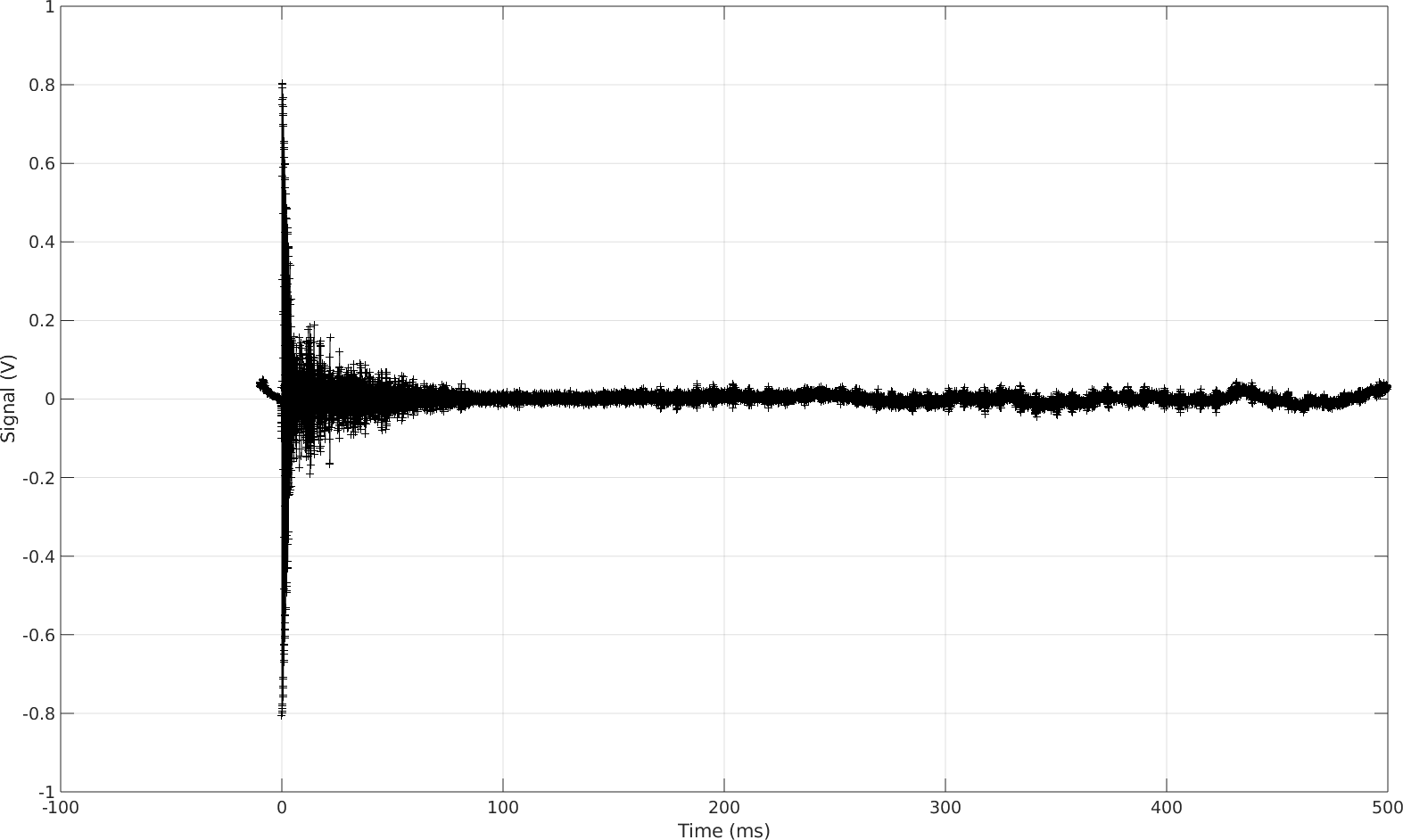
Ce signal a été enregistré dans la chambre principale, à environ 90 cm du plafond, et respectivement 110 cm et 160 cm des murs latéraux. Les deux autres murs qui ferment la pièce ont été négligés ici car ils présentent des portes, des fenêtres, des placards ou des meubles et je suppose que tous ces éléments sont propices à atténuer l’écho (par des phénomènes d’absorption ou de diffusion).
Il peut être intéressant de modéliser la propagation du son de la castagnette pour se rendre compte des ordres de grandeurs sur les temps d’aller/retour. Si on assimile ce son à une onde sphérique, nous pouvons observer le front d’onde se propager dans l’animation ci-dessous. La vitesse de propagation est celle du son au niveau de la mer (340 m/s) et les dimensions de la pièce sont du même ordre de grandeur que ceux de ma chambre. Nous faisons l’hypothèse d’une absorption maximale au niveau du sol (présence d’un lit) et d’une absorption et d’une diffusion nulles au niveau des murs et du plafond. On observe que les premiers retours du son sont très rapide (environ 5 ms) par rapport à la durée du phénomène (500 ms).
Nous pouvons faire apparaître ces différents échos sur le signal temporel. Les différents modes sont notés $(i,j)$ avec $i$ le nombre de réflexions sur le plafond et $j$ le nombre (algébrique) de réflexions sur les murs. Si $j$ est négatif, le son s’est d’abord réflechi sur le mur gauche (situé à 110 cm) et si $j$ est positif, le son s’est d’abord réflechi sur le mur droit (situé à 160 cm).
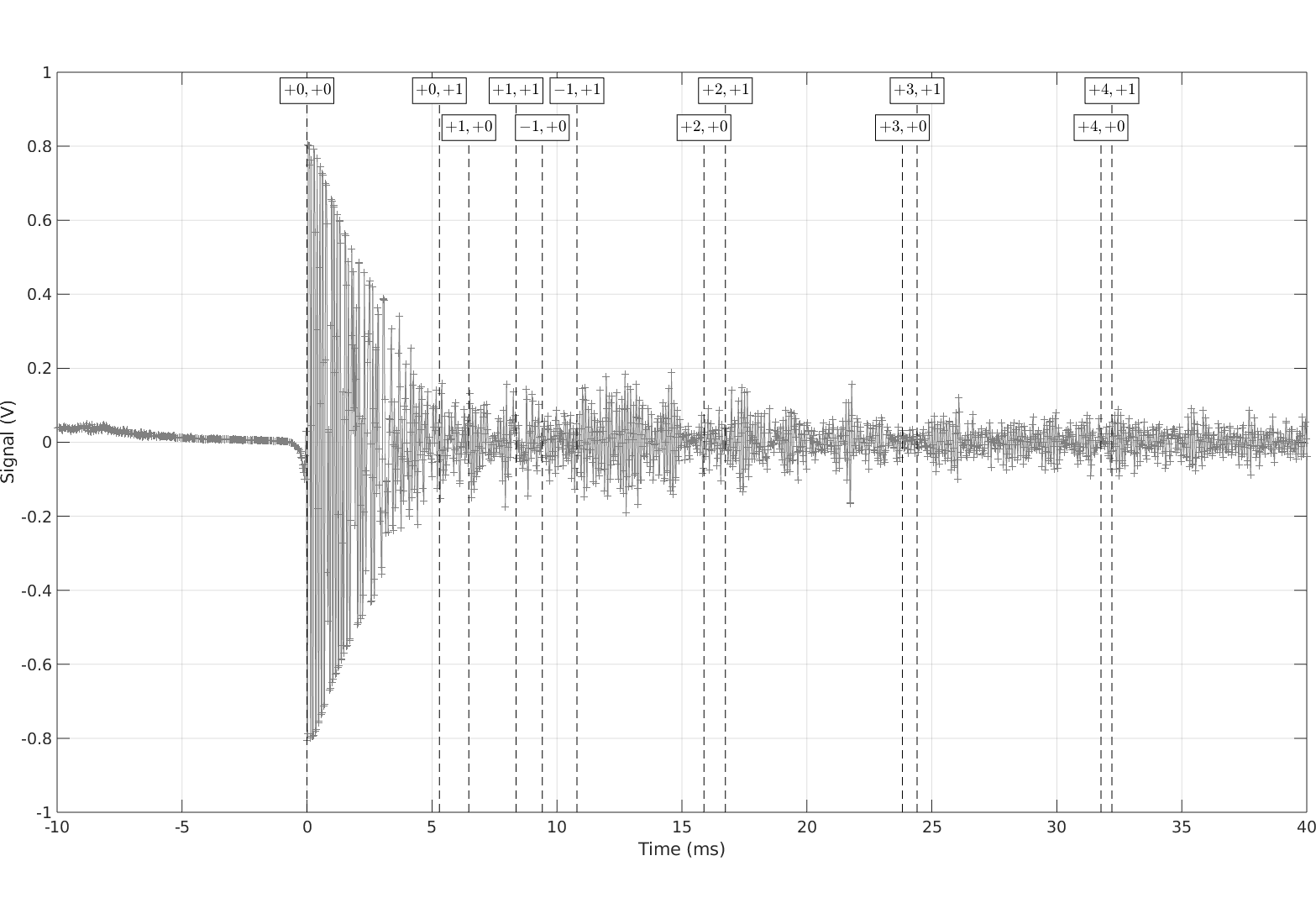
Nous remarquons que le clap initial est, lorsqu’on zoome un peu, finalement assez riche malgré une décroissance très rapide.
Par ailleurs, le signal retour s’étalant sur une durée 100 fois plus longue que le temps du premier écho, je pense que nous sommes plus sur une espèce de résonance avec un système acoustique invisible caché quelque part. Notre castagnette-dirac arrosant un peu toutes les fréquences, les fréquences de résonance du système invisible sont alors excitées et c’est précisément ce son là que nous entendons.
Une autre façon de penser ce signal consiste à considérer le signal retour comme la réponse impulsionnelle de notre système invisible suite à l’excitation par un Dirac. Quelque part, nous cherchons donc à caractériser un filtre (assurémment causal, pas nécessairement linéaire).
Voyons si nous pouvons aller un peu plus loin.
Analyse temps-fréquence
Nous calculons maintenant une densité spectrale de puissance (DSP) glissante basée sur des fenêtres temporelles de 128 points (2.9 ms) avec un overlap de 64 points et une pondération par fenêtre de Hamming. Nous calculons la racine carré du module de ce signal (donc en $V/\sqrt{Hz}$ puisque nous travaillons sur la puissance) ainsi que sa phase. Ces résultats sont présentés ci-dessous.
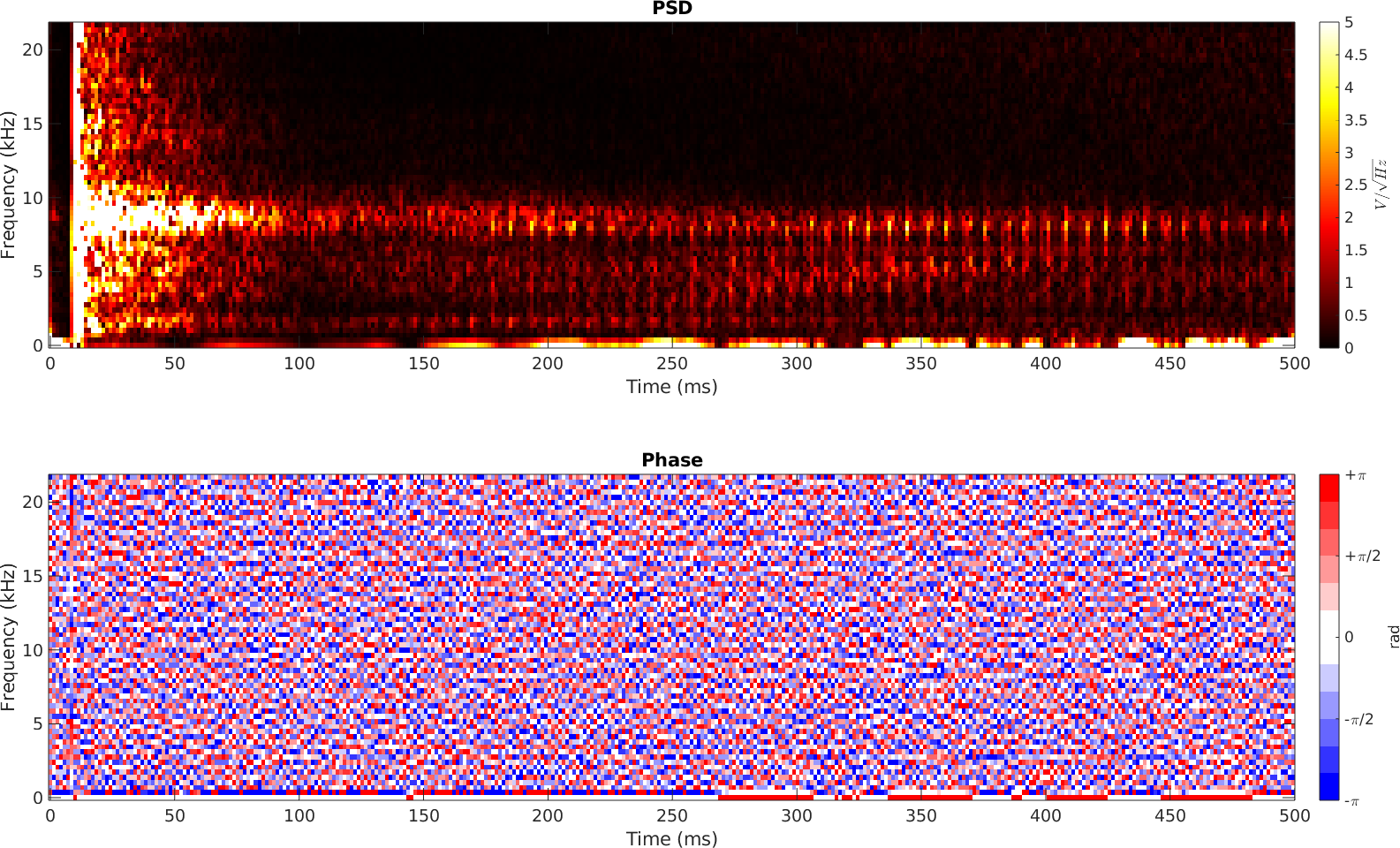
Sur la DSP, nous identifions immédiatement le Dirac qui arrose toutes les fréquences et nous voyons ensuite un contenu spectral assez riche dans les 500 ms qui suivent avec une raie assez marquée aux alentours de 8 kHz modulée en basse fréquence par une porteuse à environ 120~150 Hz. Il y a aussi tout un tas de fréquences avec une puissance non négligeable en-deça du 8 kHz mais leur signature semble moins nette. On observe en revanche toujours cette modulation basse fréquence. Pas grand chose à dire en revanche sur la phase de la DSP.
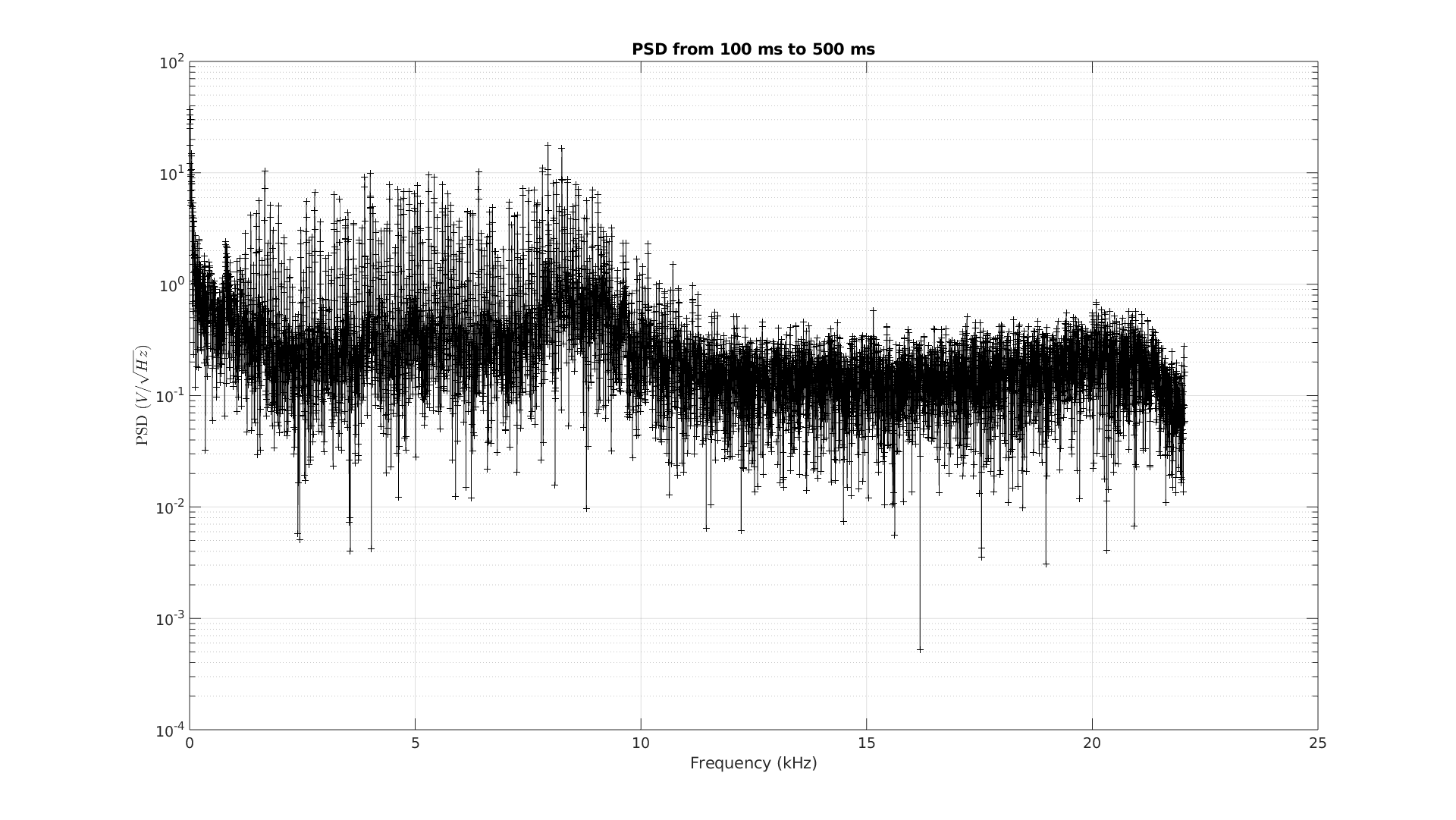
Nous pouvons également tracer la DSP sur le segment temporel qui va de 100 ms jusqu’à 500 ms. Nous obtenons alors la figure ci-dessous. Je pense que la modulation à 150 Hz introduit un dédoublement de toutes les raies, puisque :
\[2 \cos a \cos b = \cos (a+b) \cos (a-b)\]Effectivement, dans le signal ci-dessous les deux maxima autour de 8 Khz sont ainsi séparés d’environ 300 Hz ce qui est le bon ordre de grandeur.
Identification de la source du bruit
En tapant sur le plafond, j’entends comme un bruit métallique ce qui a tendance a corroborer l’hypothèse d’un système mécanique qui réagit à l’onde sonore. Si j’avais eu plusieurs smartphones, j’aurais pu faire un peu de triangulation sommaire et de problème inverse pour localiser un peu mieux l’origine du bruit mais on fait avec ce qu’on a (et ceci aurait soulevé la question de la synchronisation des enregistrements).
Ce plafond a la particularité d’être chauffant, un maillage de câbles électriques invisibles le recouvre donc. C’est probablement l’origine du bruit étrange que nous entendons.
Analogie avec la guimbarde
J’ai dit que le son que j’obtiens m’évoquait un peu le bruit d’une guimbarde. Voyons si cette analogie se justifie dans la comparaison des signaux.
Je n’ai hélas pas de guimbarde chez moi. En revanche, on peut trouver trouver des échantillons sur YouTube. J’ai trouvé un exemple sur la chaîne d’Anton Platonov et j’en ai extrait la piste sonore avec youtube-dl.
youtube-dl -x --audio-format wav --output guimbarde.wav https://www.youtube.com/watch?v=pBzIvDidTIU
J’ai ensuite isolé une “note” en sélectionnant une fenêtre temporelle de -10 ms/+500ms autour du premier maximum rencontré dans les deux premières secondes (c’est un peu artisanal mais ça fonctionne bien). Voici cet extrait :
Je calcule la DSP de ce signal avec les mêmes paramètres. Je remarque ceci dit que le signal est cette fois-ci échantillonné à 48 kHz.
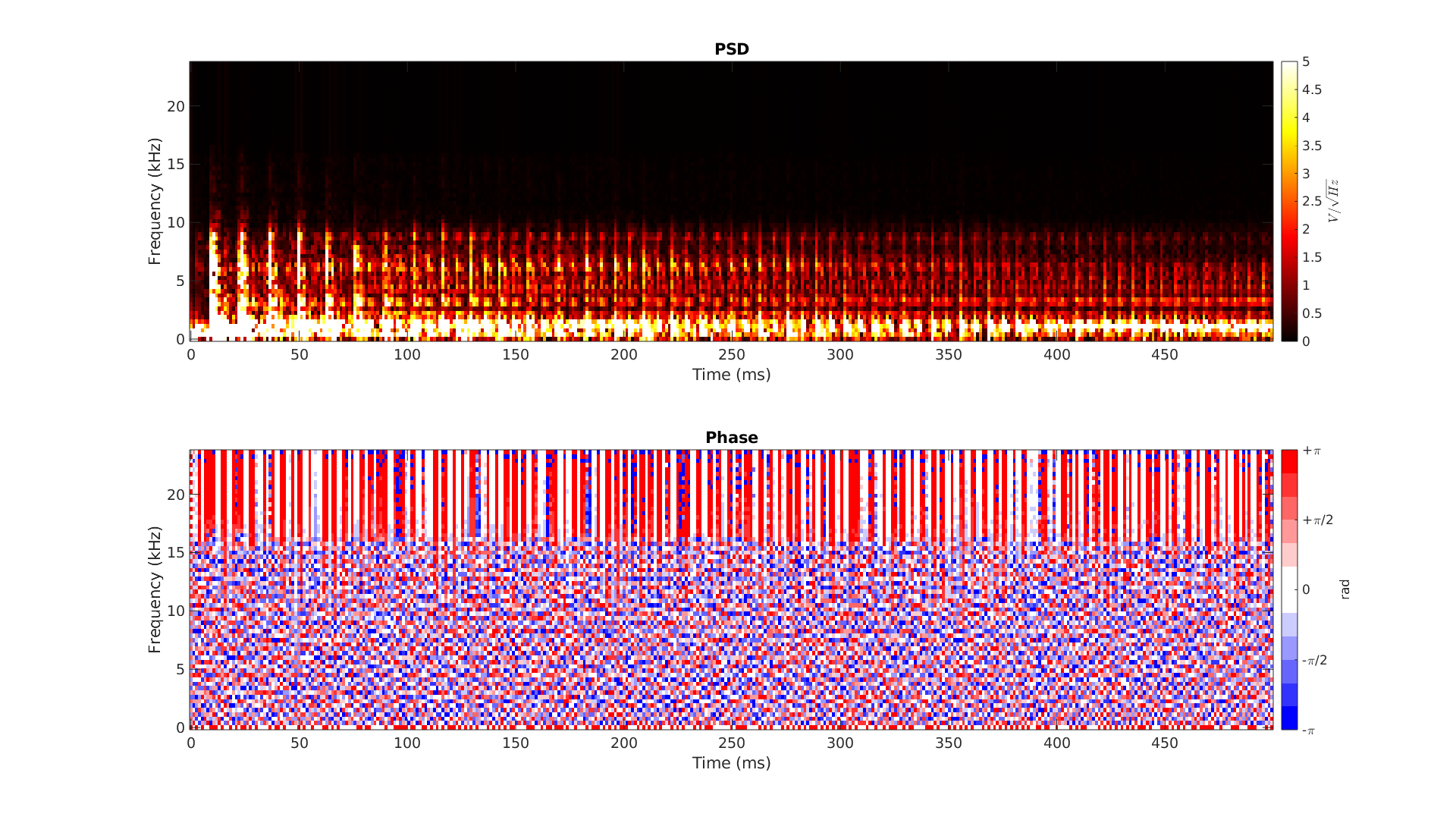
On retrouve à nouveau une plage de fréquences modulées ! La phase ne donne toujours rien de probant même si on observe quelque chose de curieux aux hautes fréquences (au-delà de 15 kHz). Un tracé de la DSP en échelle logarithmique sur le segment 100 ms-500ms nous apporte un éclairage sur ce curieux comportement : il y a une brusque coupure du contenu spectral au-delà de 15 kHz. Sans doute un effet de la compression (non conservative) du signal sonore.
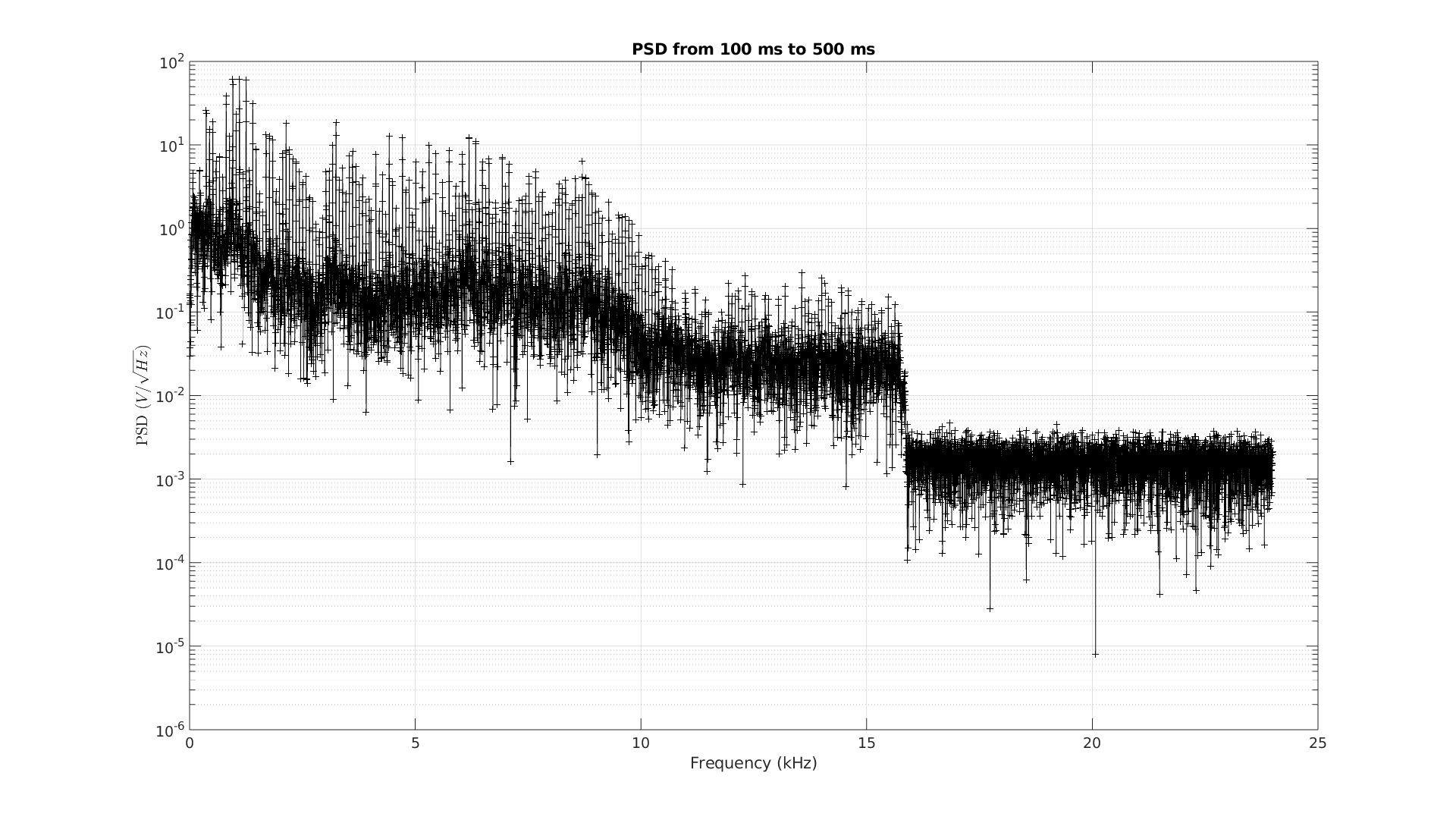
Analogie avec la règle en plastique
J’ai évoqué la règle en plastique plaquée contre un coin de table comme analogie sonore possible. Je n’ai pas de guimbarde mais j’ai une règle en plastique !
Voici le son que j’ai capturé (toujours avec mon smartphone).
Et voici la DSP, toujours calculée avec les même paramètres. On retrouve une fois de plus le même signal caractéristique ! Bon c’était assez attendu puisque les deux instruments fonctionnent de manière similaire.
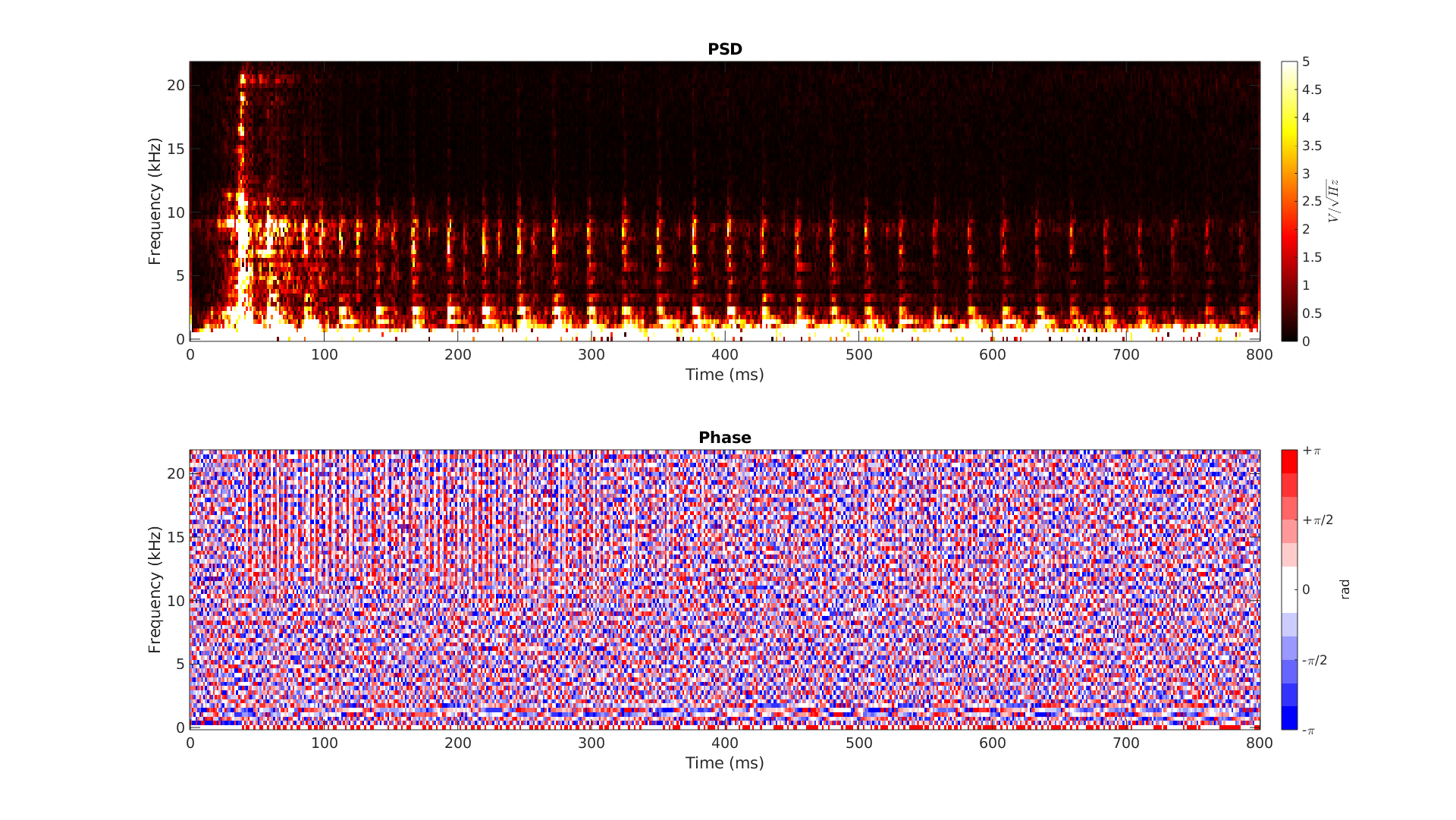
Vers un modèle de bruit
Bon, comme j’ai découvert p5.js récemment, j’ai un peu envie de le mettre à toutes les sauces.
Il existe bien une bibliothèque additionnelle permettant de gérer des signals sonores, appelée p5.sound.js mais elle a l’air assez pauvre en traitement de signal pur. On peut définir des oscillateurs de forme classique (sinusoïde, carré, triangle…) et faire une modulation en fréquence ou en amplitude… et c’est à peu près tout.
Donc en gros, faire un petit simulateur avec p5.sound.js ne donnera qu’un résultat très approximatif de ce que je souhaite modéliser. Je ne creuse pas plus cette piste mais je mets quelques liens en fin d’article si d’aventure un jour j’ai envie d’approfondir un peu ce sujet.
Pistes pour la suite ?
- Créér un modèle bruit pour voir si on arrive à reproduire la signature du son qu’on entend
- Dans l’analogie de la règle en plastique, on pourrait étudier les modes de résonance d’une poutre en vibration afin de voir si la connaissance des fréquences caractéristiques nous permet de remonter à une connaissance sur la géométrie ou la nature du système vibrant. A vue de nez, et dans la mesure où l’analogie avec la règle est pertinente, je dirais que les paramètres sous-jacents seraient : longueur caractéristique, épaisseur et largeur, module d’Young (pour l’étude de la déformation) et masse volumique (pour un éventuel bilan des forces). Mais nous n’avons que très peu d’observables (essentiellement la fréquence, peut-être aussi le temps de relaxation), donc pas sûr qu’on puisse en tirer grand chose.
Conclusion
J’ignore si tous les plafonds chauffant réagissent au 8 kHz ou bien s’il s’agit d’un défaut de mon installation (le chauffage marche super bien, ceci dit). J’ai peut-être trouvé une façon non intrusive de détecter un plafond chauffant.
Sources
Un document de l’ESPCI sur l’étude des poutres vibrantes