Je me suis récemment replongé dans une vieille BD que j’avais co-écrite au lycée et ça m’a rappelé le genre de fractales que j’essayais de tracer à l’époque sur ma calculette (une TI-83).

Plan de l’article

Introduction

Partons de l’équation paramétrique d’un cercle. En prenant $t \in [0, 2\pi]$, nous avons dans le système de coordonnées cartésiennes $(\mathbf{e_x}, \mathbf{e_y})$ :

\[\left\{\begin{array}{rcl} x_0(t)&=&\cos(t)\\ y_0(t)&=&\sin(t)\\ \end{array}\right.\]

Nous pouvons définir le vecteur tangente $\mathbf{\tau{}_0}$ par :

\[\mathbf{\tau{}_0} = -\sin{}(t)\mathbf{e_x} + \cos{}(t)\mathbf{e_y}\]

La normale $\mathbf{n_0}$ s’obtient ensuite :

\[\mathbf{n_0} = \left( \begin{array}{cc} \phantom{-}0 & \phantom{-}1 \\ -1 & \phantom{-}0 \end{array} \right) \mathbf{\tau{}_0} = \mathbf{M} \mathbf{\tau{}_0}\]

L’idée est de construire une série de N courbes. Chaque courbe $k$ est égale à la courbe $(k-1)$ sauf qu’on rajoute un signal $z_k$ sur la composante normale (aligné avec $\mathbf{n}$) donc.

\[\left\{\begin{array}{rcl} x_{k+1}(t)&=&x_k(t) + (\mathbf{n_k} \cdot \mathbf{e_x}) \times z_k(t)\\ y_{k+1}(t)&=&y_k(t) + (\mathbf{n_k} \cdot \mathbf{e_y}) \times z_k(t)\\ \end{array}\right.\]

Choisissons un $z_k$ sexy : une sinusoïde s’enroulant sur une sinusoïde par exemple. Ainsi :

\[z_k(t) = \alpha^k \, \cos(\omega^k t)\]

$\alpha$ et $\omega$ sont les paramètres de notre fractale et $k$ est son ordre.

$\alpha$ est le facteur de compression dans la reproduction du motif, c’est un réel strictement compris entre 0 et 1. En prenant $\alpha=0$, nous n’ajoutons aucune composante et les courbes successives sont toutes le même cercle.

$\omega$ de son côté est un entier naturel non-nul qui représente le nombre de lobes que nous introduisons à chaque itération. Par exemple avec $\omega=3$, nous introduirons à la première itération trois lobes autour du cercle initial. A la deuxième itération, trois lobes apparaîtront autour de chacun des trois lobes précédents conduisant donc à $3^2 = 9$ lobes et ainsi de suite. Il est nécessaire de choisir $\omega$ entier afin d’obtenir à chaque fois des courbes fermées de classe $C^\infty$ (notamment donc au point $t=2 \pi$).

Equation paramétrique à l’ordre 1

En prenant les notations réduites $c \equiv \cos(t)$ et $s \equiv \sin(t)$, nous obtenons les expressions du premier ordre de la fractale $\mathbf{X_1}$ et de sa dérivée première $\mathbf{X_1’}$ :

\[\mathbf{X_1} = \left(\begin{array}{cc} 1+ z_1 & 0\\ 0 & 1+z_1 \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right) \qquad \mathbf{X'_1} =\left(\begin{array}{cc} \dot{z_1} & - (1 +z_1)\\ (1+ z_1) & \dot{z_1} \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right)\]

La figure ci-dessous illustre quelques réalisations de fractales d’ordre 1 pour différentes valeurs du couple $(\alpha, \omega)$.

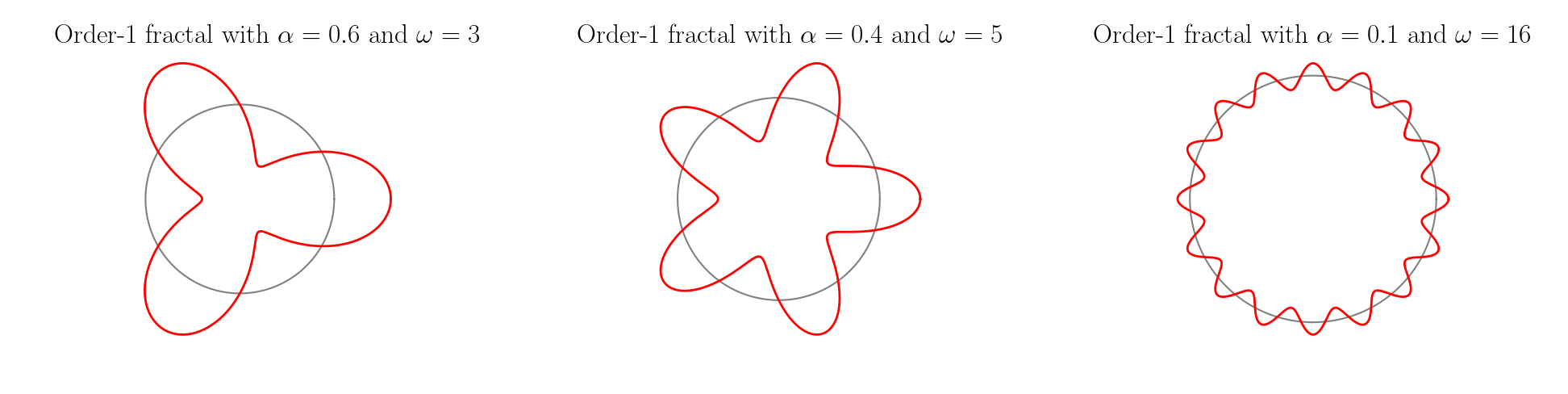
Ordre 1

On montre facilement que :

\[||\mathbf{X'_1}|| = \sqrt{\dot{z_1}^2 + (1+z_1)^2}\]

Equation paramétrique à l’ordre 2

L’équation paramètrique de la fractale d’ordre 2 $\mathbf{X_2}$ s’obtient directement :

\[\mathbf{X_2} = \mathbf{X_1} + z_2 \times \mathbf{M} \mathbf{X'_1}/||\mathbf{X'_1}||\]

Ce qui donne au final :

\[\mathbf{X_2} = \left(\begin{array}{cc} (1 +z_1) \left(1+\frac{z_2}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}}\right) & \frac{\dot{z_1} z_2}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}} \\ -\frac{\dot{z_1} z_2}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}} & (1 +z_1) \left(1+\frac{z_2}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}}\right) \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right)\]

En remarquant que $\mathbf{X_2}$ est de la forme :

\[\mathbf{X_2} = \left(\begin{array}{cc} a & b\\ -b & a \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right)\]

On peut montrer que $\mathbf{X’_2}$ sera de la forme :

\[\mathbf{X'_2} = \left(\begin{array}{cc} \dot{a}+b & -(a - \dot{b})\\ (a - \dot{b}) & \dot{a}+b \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right)\]

L’expression de $\mathbf{X’_2}$ commence à devenir assez poilue, je vous fais grâce des équations mais j’en donne juste un aperçu.

Partant de :

\[a = (1 +z_1) \left(1+\frac{z_2}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}}\right) \qquad b = \frac{\dot{z_1} z_2}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}}\]

et en remarquant que :

\[\left(\sqrt{\dot{z_1}^2 + (1+z_1)^2}\right)' = \frac{\dot{z_1} (1+ 2 z_1)}{\sqrt{\dot{z_1}^2 + (1+z_1)^2}}\]

On tombe par exemple sur l’expression suivante de $\dot{a}$ :

\[\dot{a} = \dot{z_1} \left(1+\frac{z_2}{||\mathbf{X'_1}||}+(1+z_1)\right) \left( \frac{\dot{z_2}||\mathbf{X'_1}||^2 - \dot{z_1}z_2 (1+2z_1)}{||\mathbf{X'_1}||^3}\right)\]

Quoiqu’il en soit, voici ci-dessous quelques réalisations de fractales d’ordre 2 pour différentes valeurs du couple $(\alpha, \omega)$.

Ordre 2

Equation pour un ordre quelconque

L’équation caractéristique de la fractale d’ordre $k$ s’établit récursivement en fonction des caractéristiques de la fractale d’ordre $k-1$. On a ainsi de façon générale :

\[\mathbf{X_k} = \mathbf{X_{k-1}} + z_k \times \mathbf{M} \mathbf{X'_{k-1}}/||\mathbf{X'_{k-1}}||\]

Le calcul de $\mathbf{X_k}$ va faire intervenir la dérivée de $\mathbf{X’_{k-1}}$ et, de proche en proche, on va remonter à la dérivée $k^\textrm{eme}$ de $\mathbf{X_0}$, ainsi que l’illustre la figure ci-dessous.

Calcul pyramidial

Les coefficients de pondérations feront apparaître les termes suivants (potentiellement croisés) :

  • en $(z_1, z_2, \dots, z_k)$,
  • en $(\dot{z_1}, \dot{z_2}, \dots, \dot{z}_{k-1})$,
  • en $(\ddot{z_1}, \ddot{z_2}, \dots, \ddot{z}_{k-2})$
  • etc.
  • jusqu’au dernier terme en $z_1^{(k)} = \textrm{d}^k z_1 / \textrm{d}t^k$

Ce qui complexifie terriblement les équations ici c’est la normalisation de la dérivée. En toute généralité, il reste ceci dit possible de factoriser tout ça. Remarquons par exemple que :

\[\ddot{z} = - \omega^2 z\]

De la même façon, il devrait être possible (peut-être !) d’utiliser les formules de duplication d’angle pour exprimer les différents $z_k$ en fonction d’une racine commune.

Dans l’immédiat, il est possible d’approximer l’allure de la fractale d’ordre $k$ en ne connaissant qu’un ensemble de points de la fractale d’ordre $k-1$. L’idée est de reconstituer une approximation fiable de la dérivée par différence finie. Ceci soulève deux points importants :

  1. d’une part, nous introduisons inévitablement des erreurs qui vont se propager d’une fractale à une autre,
  2. d’autre part, on le devine, les courbes vont vite devenir très agitées et il est à prévoir que, partant d’une connaissance parfaite de la fractale d’ordre $k$, le calcul fiable des dérivées point à point pour le calcul de la fractale d’ordre $k+1$ demandera une couverture de plus en plus fine.

Le théorème de Nyquist-Shannon nous indique que le volume $N$ de points nécessaires pour correctement échantillonner une fractale d’ordre $k$ et de paramètres $(\alpha, \omega)$ suit une loi de la forme suivante :

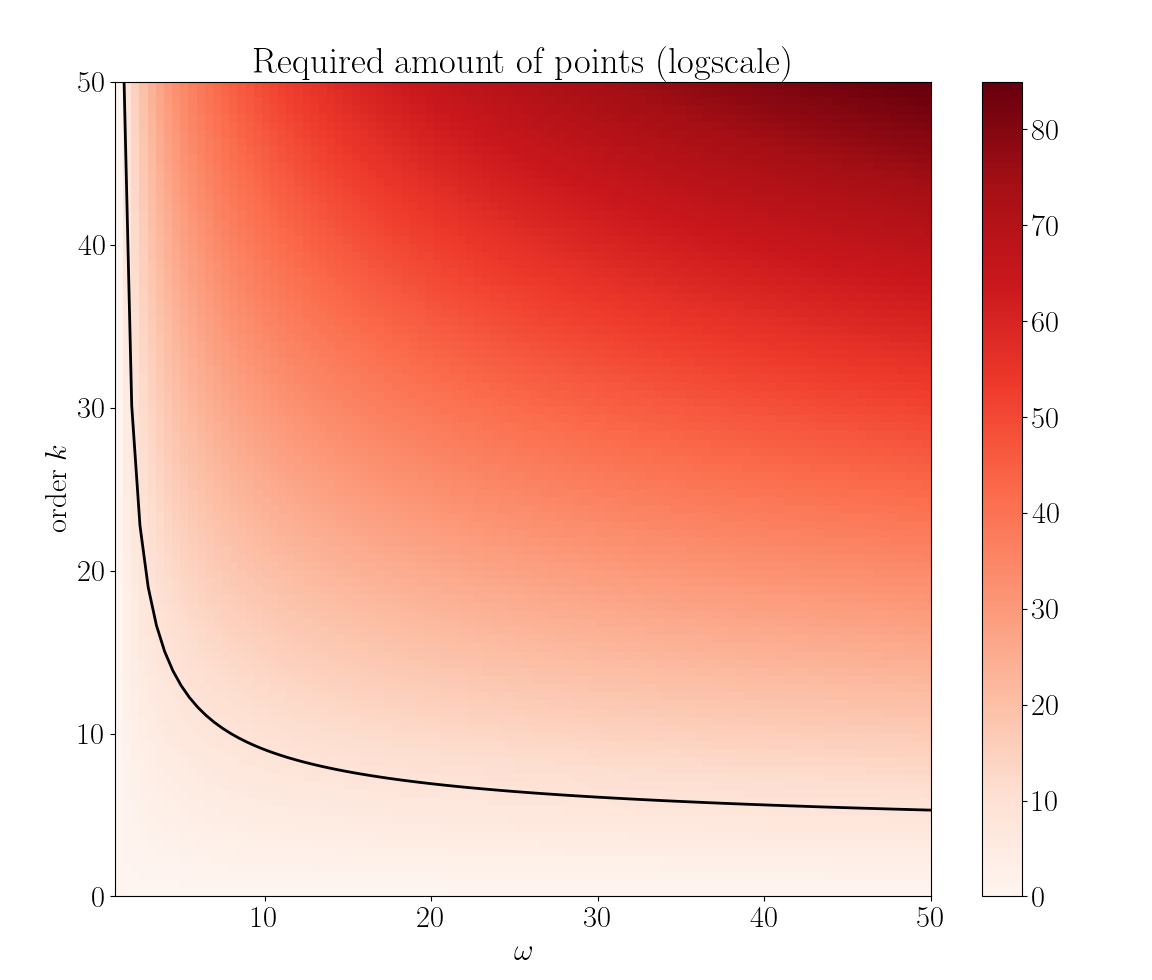
\[N \propto \omega^k\]

La figure ci-dessous illustre la variation de $N$ en échelle logarithme sur une grille de valeur de $\omega$ (en abscisses) et d’ordre (en ordonnées). La courbe noire représente un seuil limite (arbitraire) de un milliard de points. On voit bien que nous sommes très vite limités ! Afin de limiter un peu la casse, on pourrait tirer parti des symétries des courbes pour diminuer ce volume de points, mais nous ne gagnons là qu’un simple facteur diviseur. On pourrait aussi, comme le font les algorithmes de plongées sur l’ensemble de Mandelbrot, se limiter à un domaine de plus en plus restreint de la fractale.

Volume de points nécessaires

Voici quoiqu’il en soit, quelques figures que nous obtenons de cette façon :

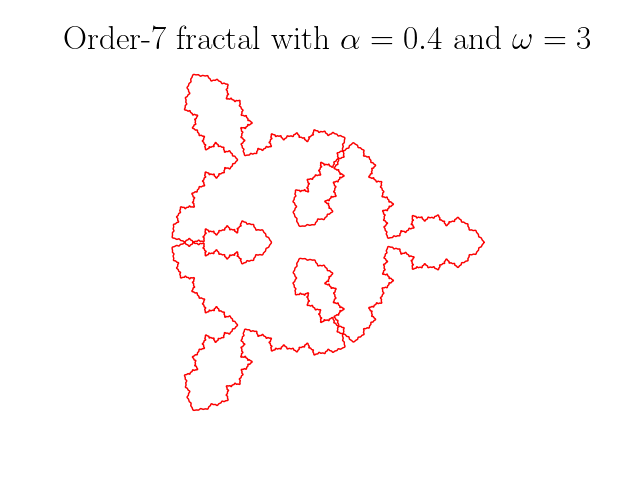
Exemple 1 Exemple 2 Exemple 3

Réflexion autout de la paramétrisation de nos fractales

Nous avons vu que l’équation d’une fractale d’ordre quelconque sera toujours de la forme suivante :

\[\mathbf{X_k} = \left(\begin{array}{cc} a & b\\ -b & a \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right)\]

Avec $a$ et $b$ des paramètres dynamiques (i.e. qui varient avec $t$). Si on fixe $a$ et $b$ et qu’on laisse varier $c$ et $s$, on s’aperçoit que $\mathbf{X_k}$ est de norme constante : $\mathbf{X_k}$ décrit un cercle de rayon $R = \sqrt{a^2+b^2}$. En effet :

\[\mathbf{X_k} \cdot \mathbf{X_k} = a^2+b^2 = R^2\]

On montre alors que $\mathbf{X_k}$ peut se mettre sous la forme suivante :

\[\mathbf{X_k} = R \left(\begin{array}{cc} \cos \theta & - \sin \theta\\ \sin \theta & \cos \theta \end{array}\right) \left(\begin{array}{c} c\\ s \end{array}\right)\]

avec

\[\tan \theta = -b/a\]

Décrire notre fractale c’est donc renseigner un rayon $R$ et un déphasage $\theta$. Ainsi, lorsque le couple $(c,s)$ décrit le cercle unité, notre fractale va effectuer des aller/retour, ce qui se traduira par un $\theta$ tantôt positif, tantôt négatif.

A titre d’illustration, voici comment varient $R$ et $\theta$ pour notre fractale d’ordre 2 et de paramètres $\alpha = 0.3$ et $\omega = 5$. Initialement la courbe démarre avec un déphasage nul et un rayon d’environ $1.4$. Le rayon va osciller (apparemment de façon symétrique) autour de la valeur $1$ (qui représente le cercle unité). La phase également oscille autour de la valeur $0$. Ces deux courbes font naturellement apparaître des motifs fractals.

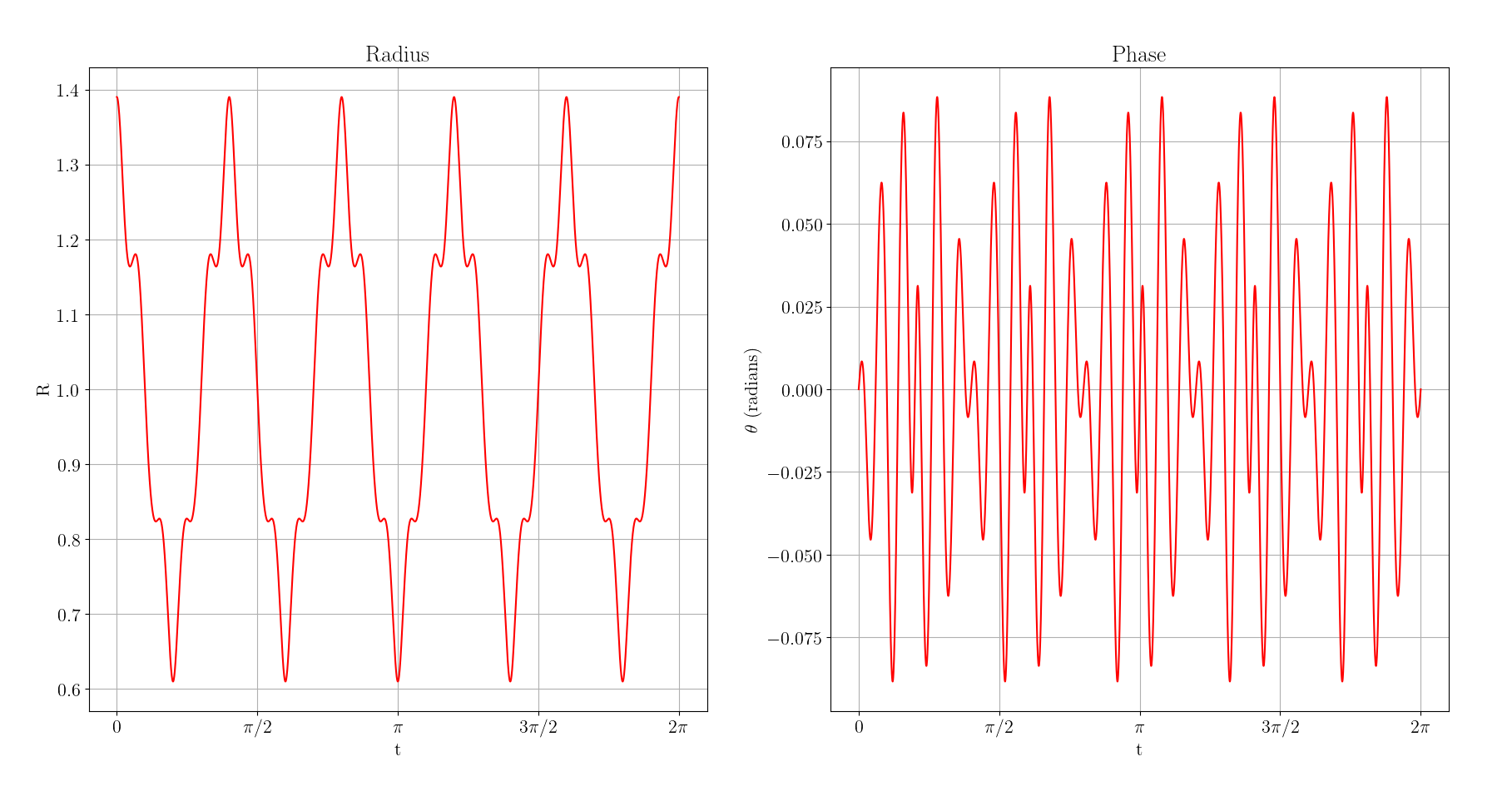
Animation Rayon et Phase

Pour aller plus loin

Au lieu d’injecter une sinusoïde qui se contracte, on pourrait envisager d’injecter une combinaison linéaire de fonctions trigonométriques. Les décompositions en série de Fourier nous permettent ainsi d’explorer à peu près n’importe quel motif périodique.

Partons par exemple du signal suivant. Nous avons choisi la hauteur $h$ du triangle égale à $\frac{\pi}{2} \sqrt{3}$, afin d’avoir un triangle équilatéral.

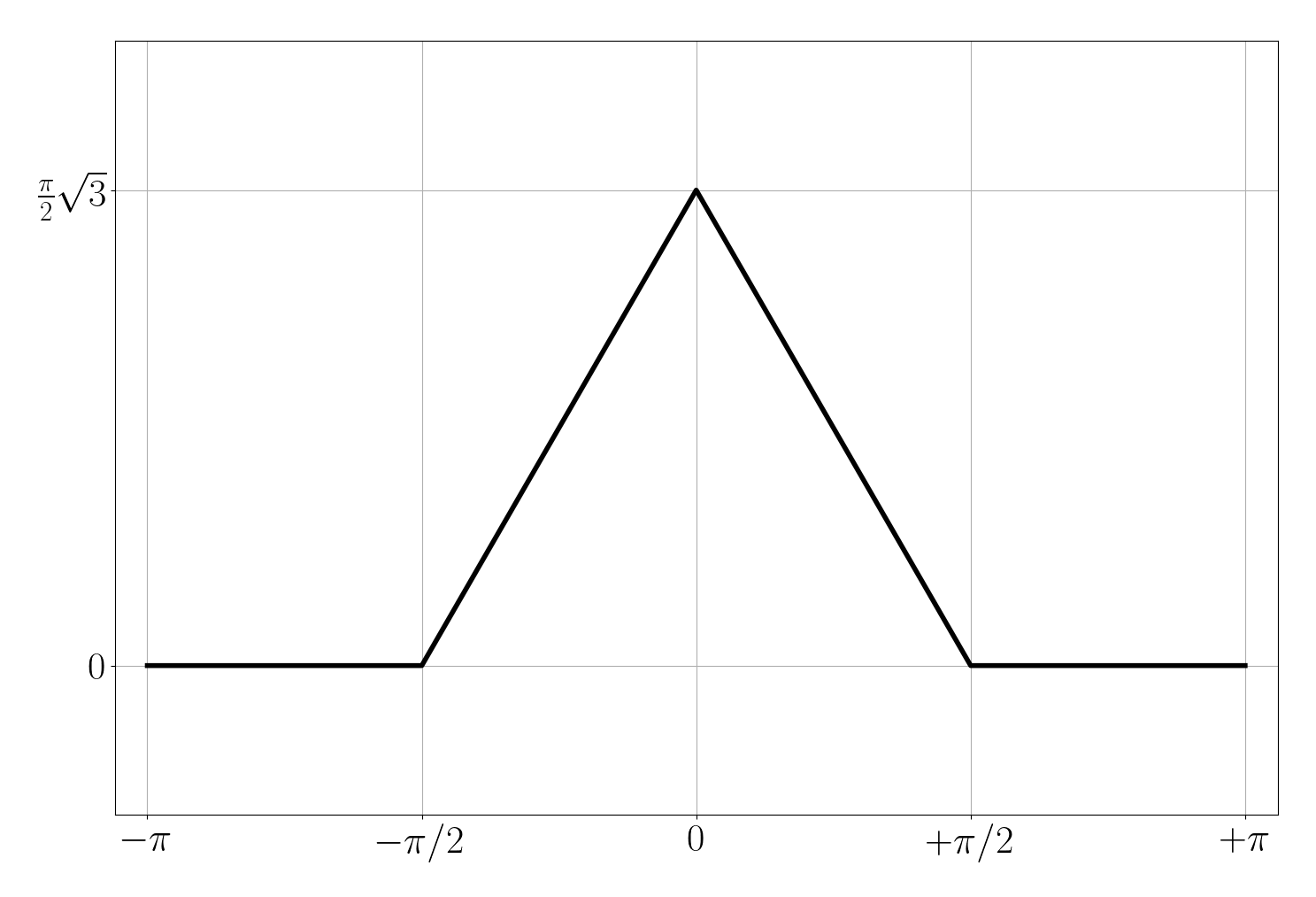
Signal triangle

C’est un signal $2\pi$-périodique que nous pouvons décomposer en série de Fourier. En remarquant que ce signal est pair, seuls les coefficients réels en cosinus seront non-nuls. On écrit :

\[z(t) = a_0 + \sum_{k=0}^{N} a_n \cos(n t)\]

Un petit calcul nous donne :

\[a_0 = \sqrt{3} \frac{\pi}{8}\] \[a_n = \frac{4h}{n^2\pi^2} \left( 1 - \cos(n\frac{\pi}{2}) \right)\]

L’allure des 12 premiers coefficients de Fourier ainsi obtenus est tracée ci-dessous. On remarque que ces coefficients sont nuls lorsque le degré est un multiple de 4, c’est à dire $a_{4k} = 0$. Ceci provient du terme en $\left( 1 - \cos(n\frac{\pi}{2}) \right)$.

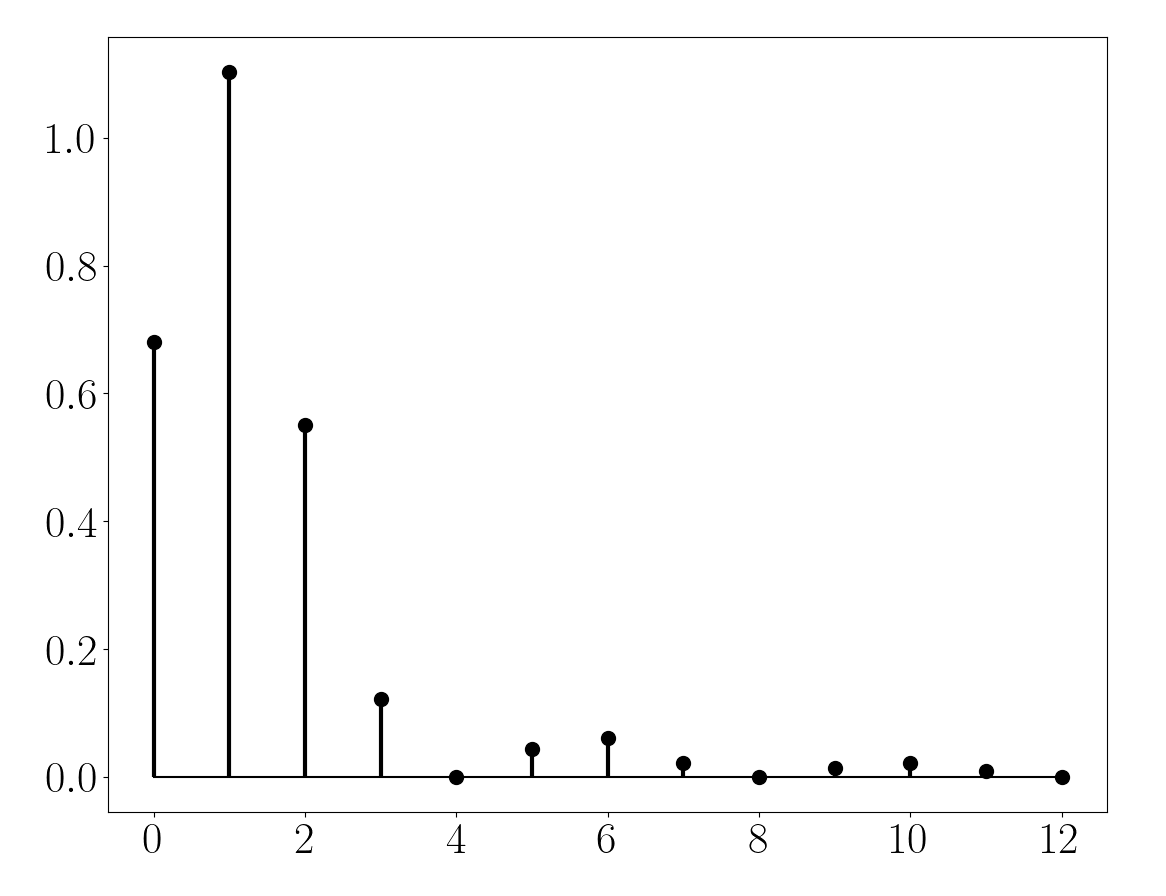
Coefficients de Fourier

La reconstruction du signal triangle par une série de Fourier tronquée est donnée ci-dessous pour un degré variant de 0 (i.e. la valeur moyenne du signal) jusqu’à 12. C’était attendu, les résidus sont localisés au niveau des transitions brusques du signal. Ceci pourra nous poser problème au voisinage de ces points, en particulier lorsqu’il s’agira de calculer les normales.

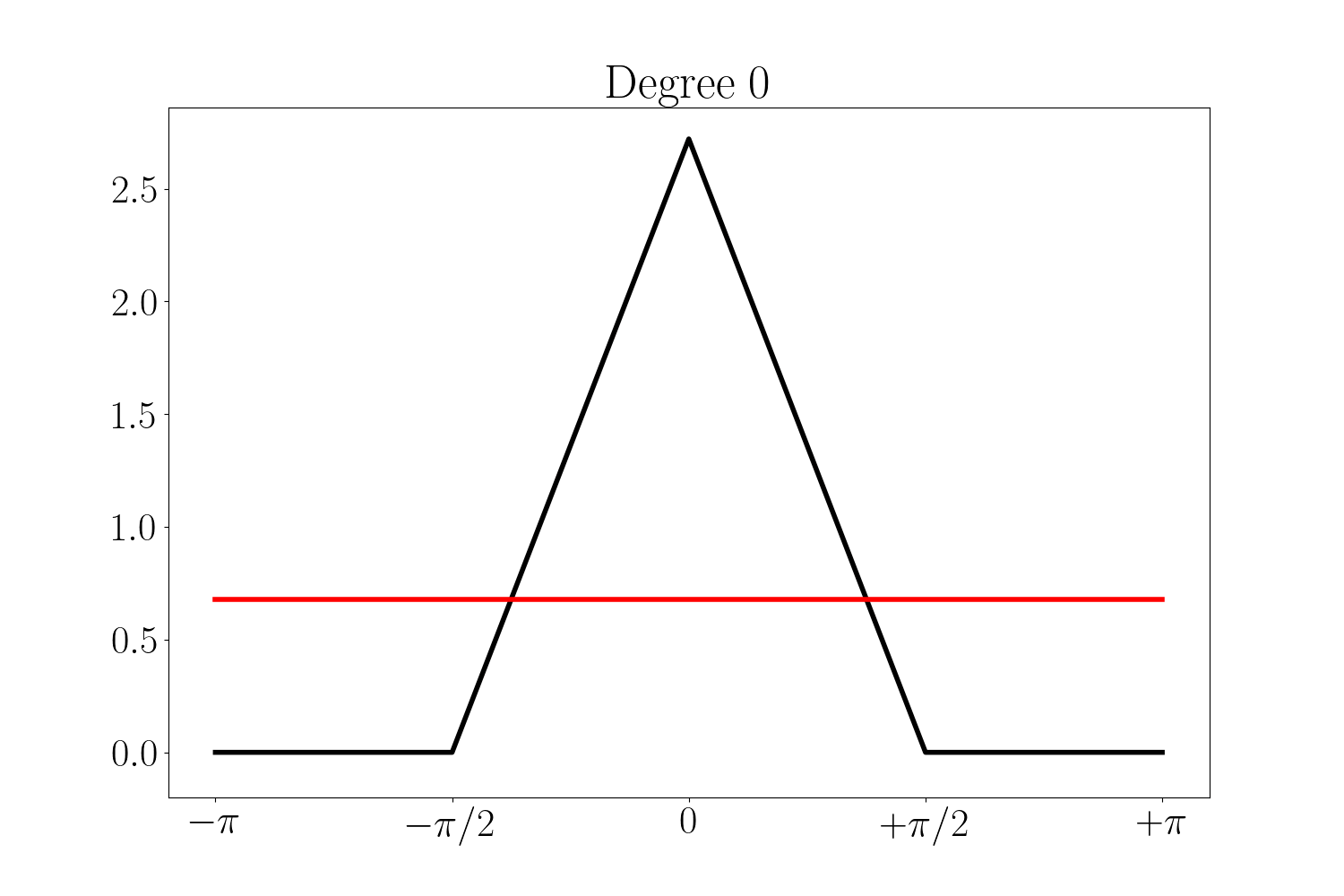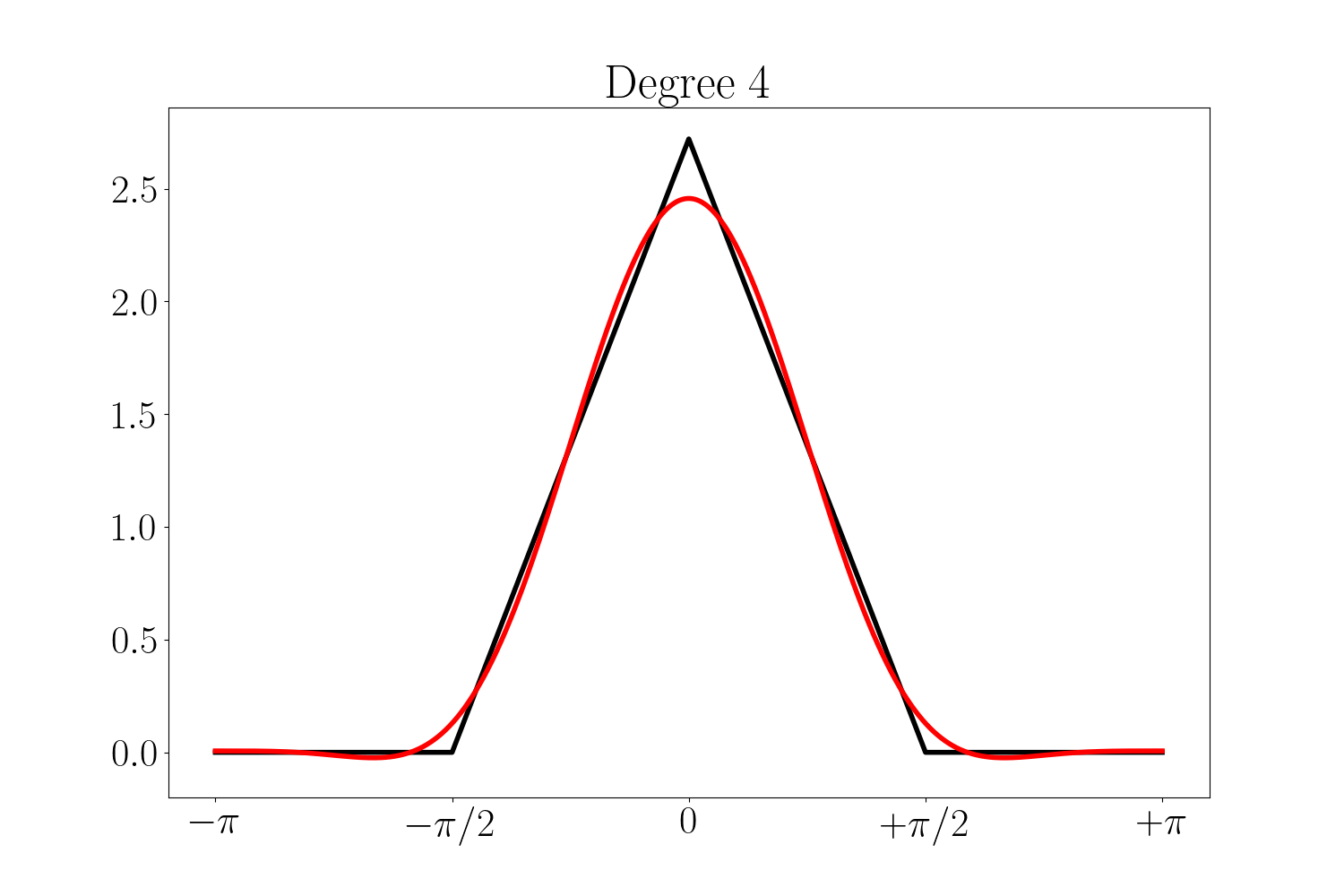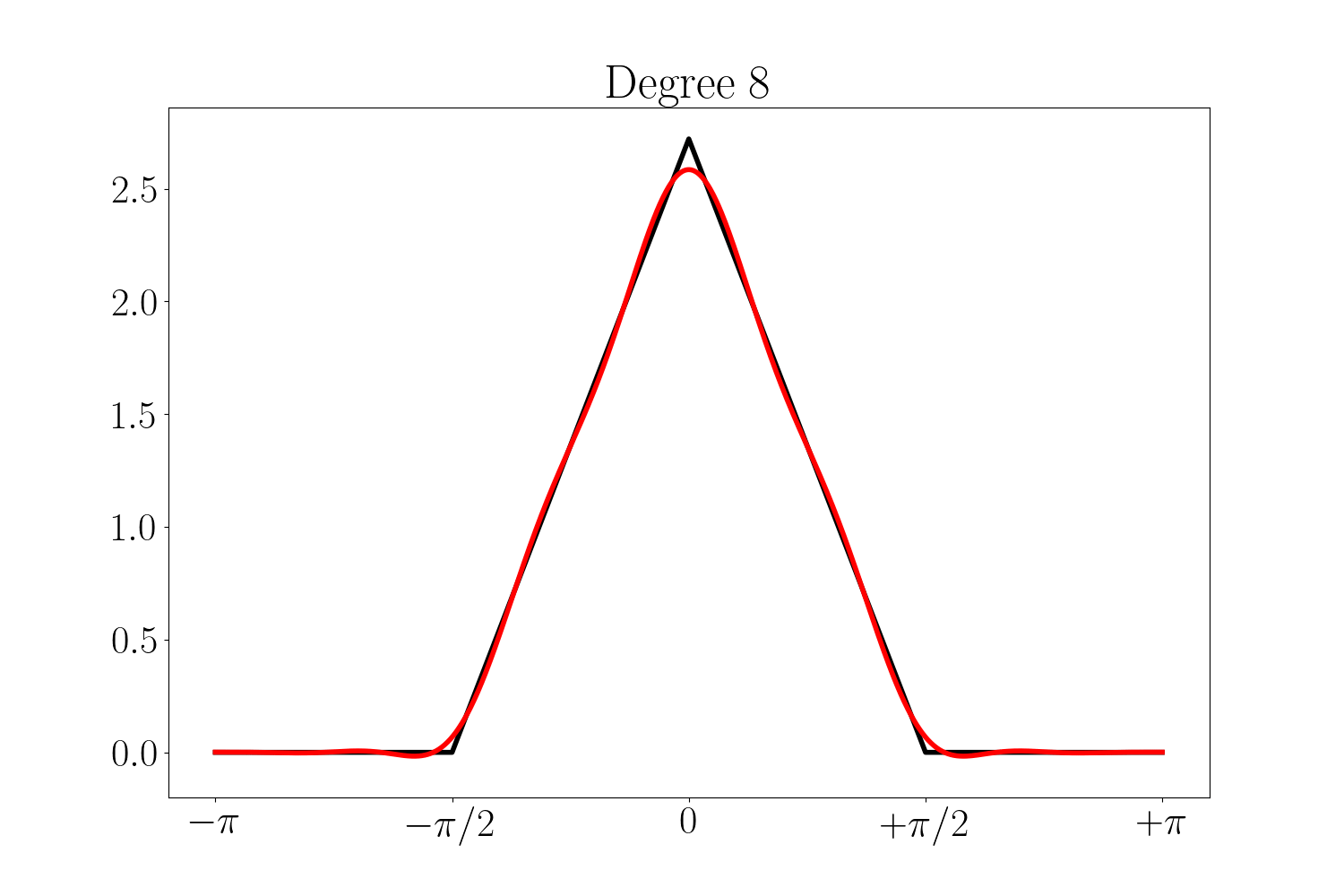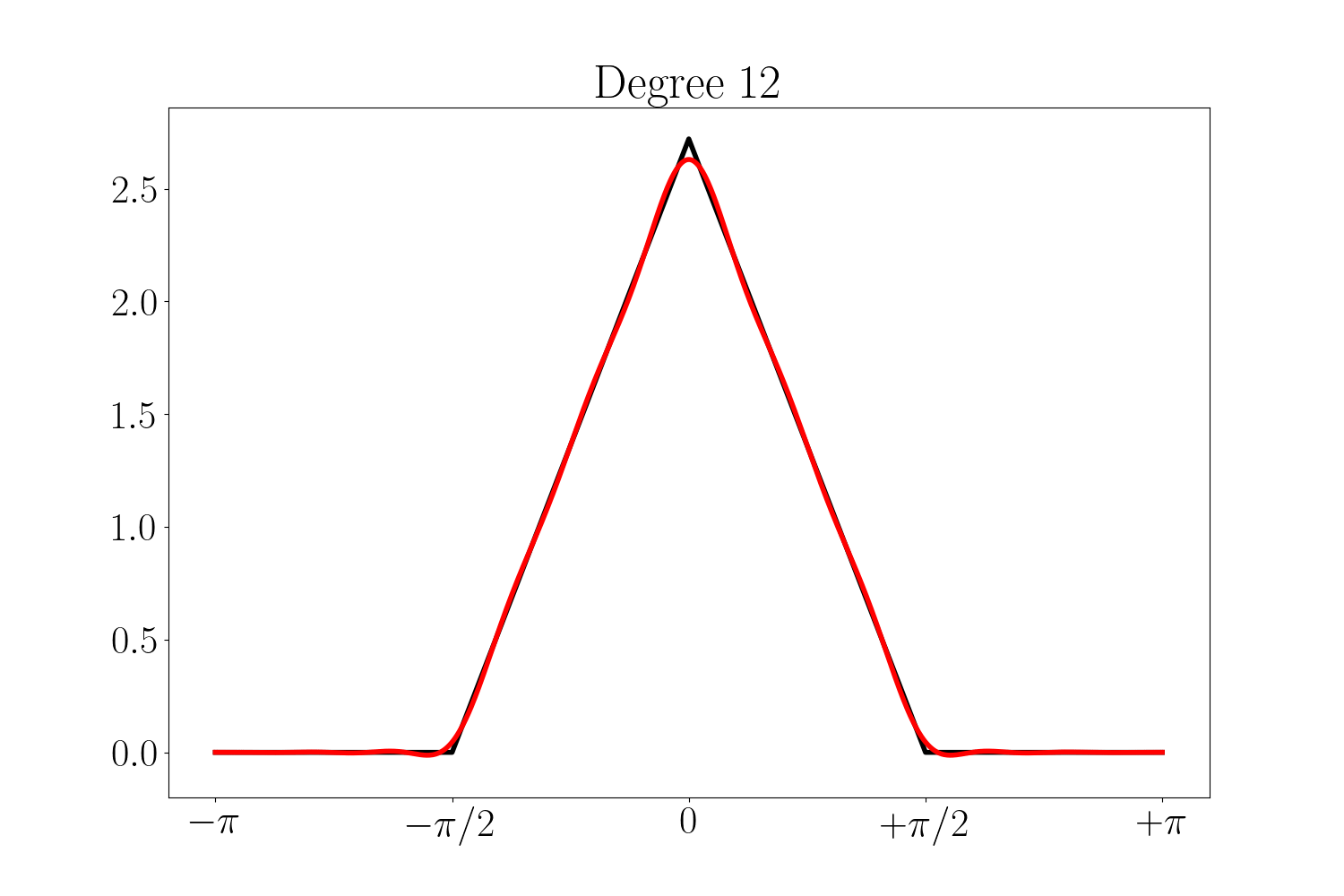
Approximation jusqu'au degré 12

En tout cas, si nous nous limitons aux séries tronquées jusqu’au degré 18, nous pouvons utiliser la définition suivante du signal $z_k$

\[z_k(t) = \alpha^k a_0 + \sum_{p=0}^{18} \alpha^k a_p \cos(\omega^k p t)\]

Et voici l’allure des fractales que nous obtenons en prenant par exemple $\alpha = 0.3$ et $\omega = 8$ et en poussant jusqu’à l’ordre 3. Choisir un $\omega$ élevé permet d’éviter de trop déformer nos triangles en les enroulant sur le cercle unité. Il est à noter que si nous étions parti d’un triangle équilatéral comme signal de départ, nous aurions obtenus in fine quelque chose qui ressemblerait un peu à un flocon de Koch mais qui présenterait d’une part la particularité d’être de classe $C^{\infty}$ à chaque itération et d’autre part de présenter des oscillations au voisinage des points de discontinuité de la dérivée.

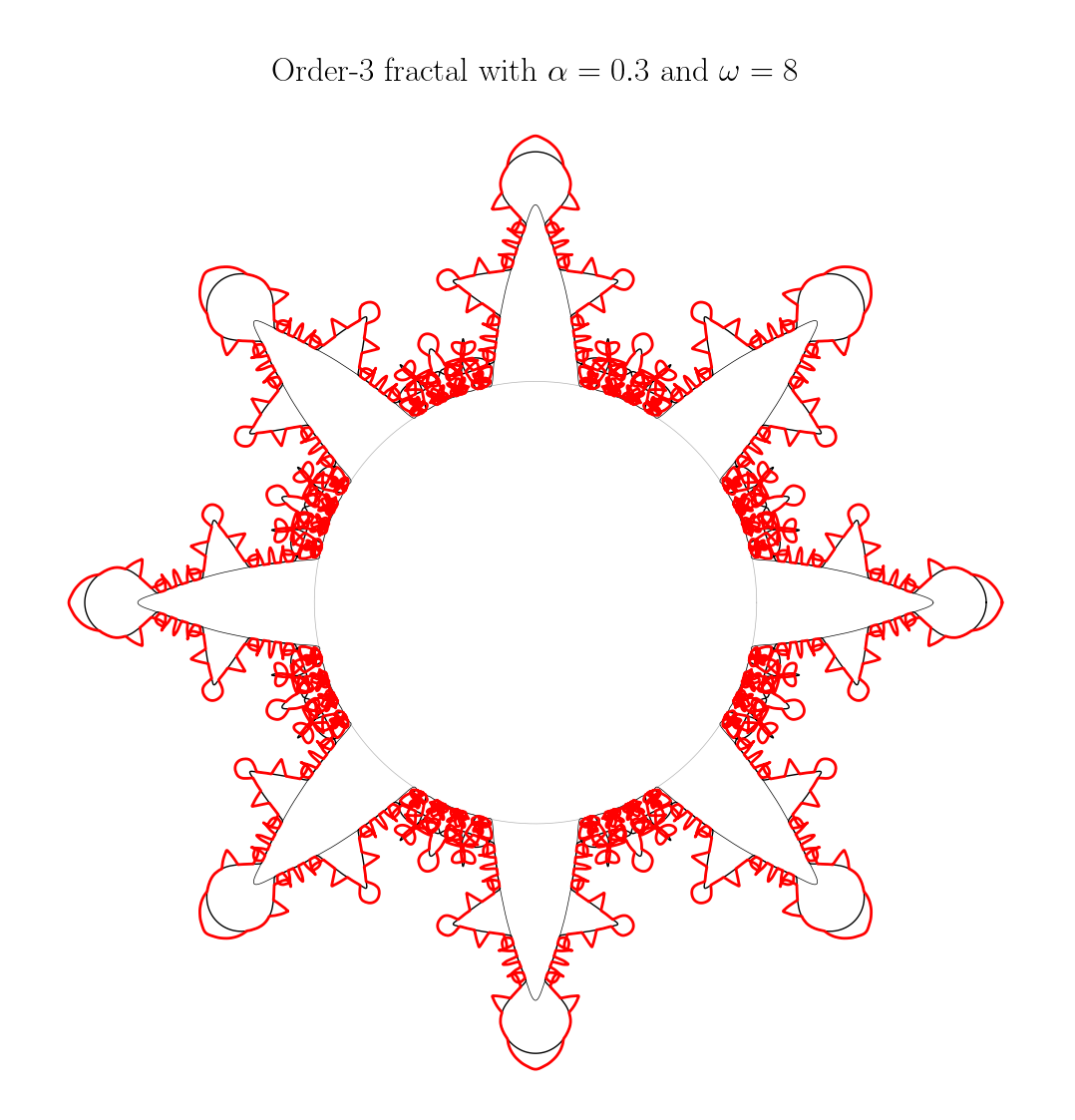
Fractale basée sur une série de Fourier tronquée

Nous remarquons au passage que les triangles n’ont pas l’air très équilatéraux. Dans mon calcul, je me suis basé sur un signal $2\pi$-périodique mais lors des différentes itérations nous manipulons des signaux de période $\omega^k$, il y a un petit facteur correctif à appliquer. On peut corriger ça rapidement en fixant le paramètre $\alpha$ à chaque itération et en utilisant la loi de dilatation de l’échelle temporelle (une contraction en temporel équivaut à une dilatation en fréquentiel). Auquel cas, on obtient des courbes un peu plus jolies.

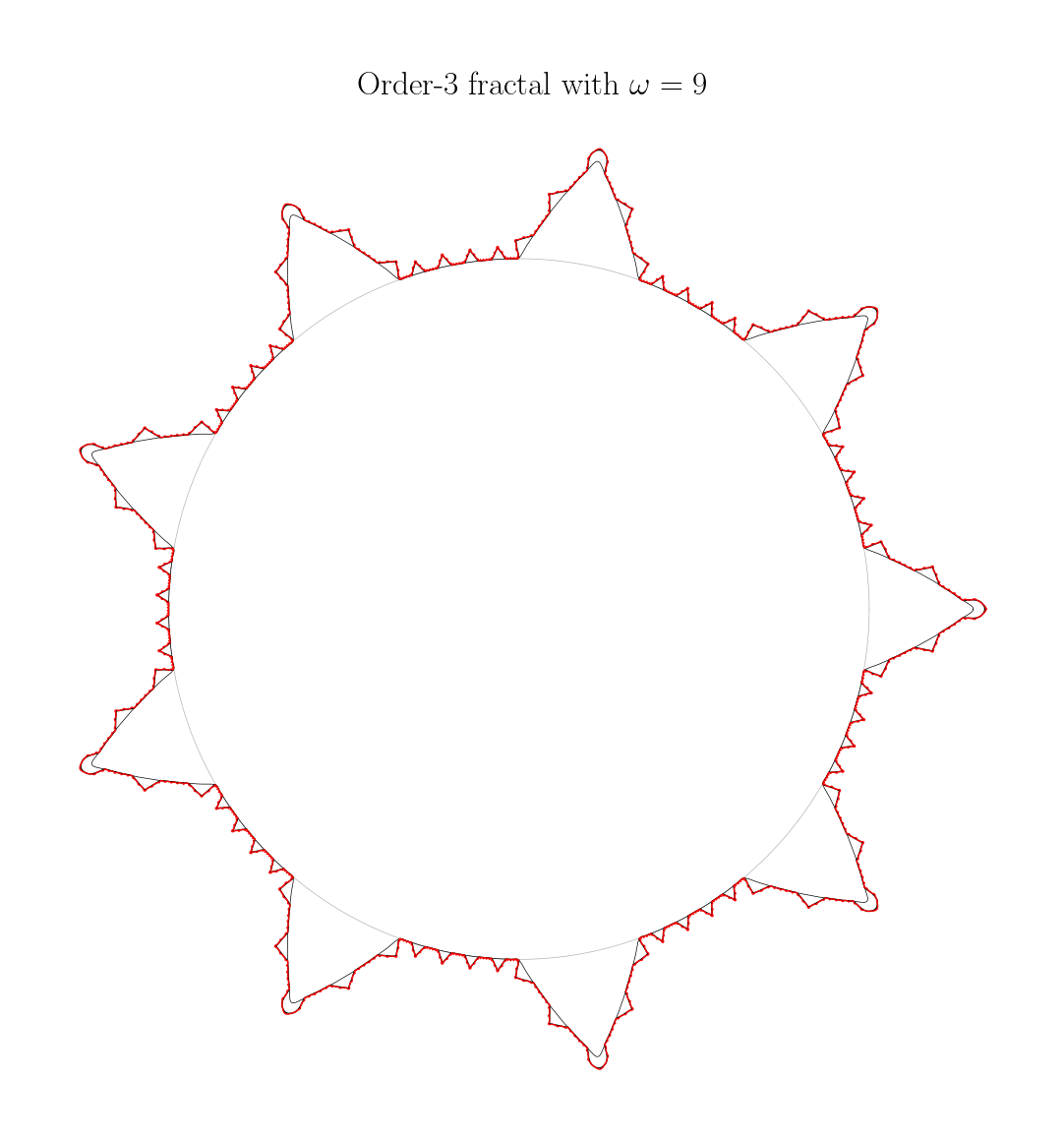
Fractale basée sur une série de Fourier tronquée

Un zoom sur une section de la courbe rouge (d’ordre 3) met bien en évidence la répétition du motif.

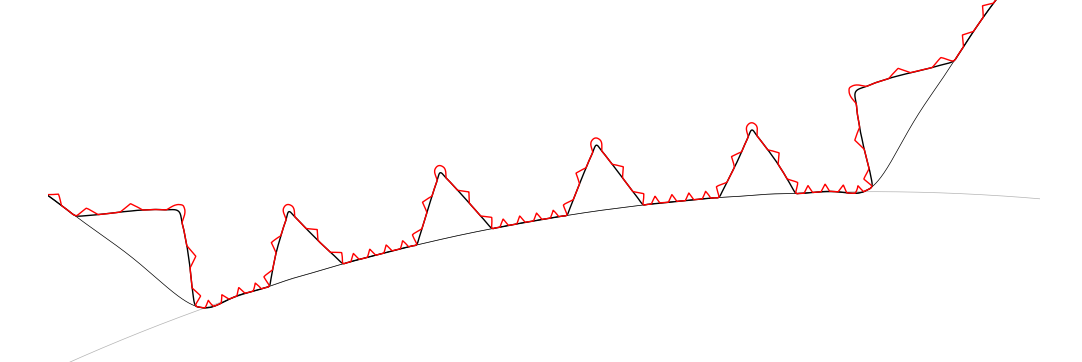
Fractale basée sur une série de Fourier tronquée

Pour être parfait, il aurait fallu partir d’un template initial plus adapté (afin d’avoir, un peu comme le flocon de Koch, un nouveau triangle sur chaque segment de polygone). Mais enfin, l’idée de base de cette dernière section était d’ouvrir un peu la discussion et de montrer qu’on pouvait empiler autre chose que de simples sinusoïdes et utiliser par exemple des triangles (ou en toute rigueur des approximations de triangle).

Code en python

Voici ci-dessous les codes que j’ai développé pour tracer les fractales présentées dans cet article. Sur mon Github se trouve également une petite interface minimaliste pour piloter tout ça.

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon Apr 26 11:59:42 2021

@author: donutman
@licence: GPL
"""
import numpy as np
from matplotlib import pyplot as plt, rc

def get_analytic_1(a, w, t):
    c = np.cos(t)
    s = np.sin(t)
    z  = a*np.cos(w*t)
    
    x = c*(1+z)
    y = s*(1+z)
    return (x,y)

def get_analytic_2(a, w, t):
    c = np.cos(t)
    s = np.sin(t)
        
    x0 = c
    y0 = s
    
    z1   =  a*np.cos(w*t)
    z1p  = -a*w*np.sin(w*t)
    z1pp = -a*w*w*np.cos(w*t)
    
    z2  =  a*a*np.cos(w*w*t)
    z2p = -a*a*w*w*np.sin(w*w*t)
    
    x1 = c*(1+z1)
    y1 = s*(1+z1)
    
    n1 = np.sqrt(z1p*z1p + (1+z1)*(1+z1))

    x2 = (1+z1)*(1+z2/n1)*c + z2/n1*z1p*s
    y2 = -z2/n1*z1p*c + (1+z1)*(1+z2/n1)*s
    
    return (x2, y2)


def plot_fractal(order, a, w):
    t = np.linspace(0, 2*np.pi, 1000*order)
    dt = t[1]-t[0]
    
    if order==1:
        (x, y) = get_analytic_1(a, w, t)
        xp = 0
        yp = 0
    elif order==2:
        (xp, yp) = get_analytic_1(a, w, t)
        (x, y)   = get_analytic_2(a, w, t)
    else:
        (x, y) = get_analytic_2(a, w, t)
    
        for k in range(3, order+1):
            z = np.power(a, k-1)*np.cos(np.power(w, k-1)*t)
            dx = np.diff(x, append=x[0])
            dy = np.diff(y, append=y[0])
            
            nx = +dy/(np.sqrt(dx*dx+dy*dy))
            ny = -dx/(np.sqrt(dx*dx+dy*dy))
            
            xp = x
            yp = y
            
            x = x + nx*z
            y = y + ny*z
            
    plt.figure()
    plt.plot(xp, yp, '-', color=0.7*np.array([1,1,1]), lw=0.5)
    plt.plot(x, y, 'r-', lw=1)
    plt.axis('equal')
    plt.axis('off')
    plt.title(r'Order-%d fractal with $\alpha = %2.1f$ and $\omega = %d$'
    		% (order, a, w), fontsize=24)