Récemment j’ai du découper un plan de travail de cuisine. Le problème ? Un des angles du mur sur lequel le plan de travail allait reposer n’est pas droit. N’ayant pas d’outil pour mesurer les angles, il a fallu ruser pour déterminer l’angle de coupe sans autre instrument qu’un mètre et un niveau à bulle. C’est un petit problème de géométrie assez simple mais dont la résolution a été très satisfaisante ! Ici je vais un tout petit peu plus loin afin d’estimer la précision attendue par ma méthode.

Présentation du problème

Le plan de travail et son environnement sont présentés dans la figure ci-dessous. Les angles et les rapports de longueur sont conformes à la réalité et on constate tout de suite que le mur de droite n’est pas vraiment droit et forme un angle inférieur à 90° avec le mur du fond. Nous notons $\gamma$ cet angle.

Position du plan de travail

Calcul de l’angle $\gamma$ et du décalage $h$

Afin d’estimer la valeur de $\gamma$, on va tracer un triangle virtuel $ABC$, le plus grand possible et dont l’angle $\gamma$ est porté par $\widehat{BCA}$. Nous notons $a$ la longueur de $BC$, $b$ la longueur de $AC$ et $c$ la longueur de $AB$.

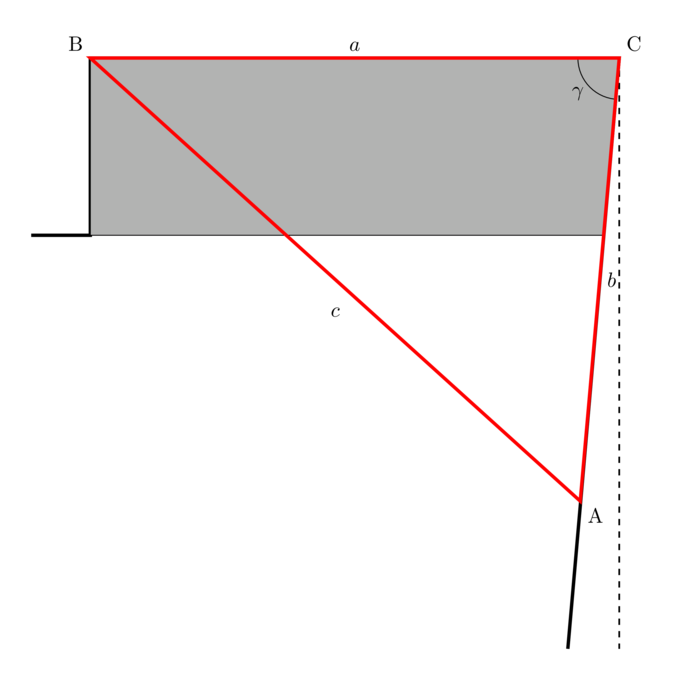
Définition du triangle ABC

Voici les mesures que j’ai obtenues :

Côté Longueur (cm)
$a$ 179
$b$ 190
$c$ 250

Le théorème d’Al-Kashi (ou théorème de Pythagore généralisé) nous permet alors d’avoir une expression de l’angle $\gamma$ en fonction des longueurs $a$, $b$ et $c$ :

\[\gamma = \textrm{arccos}\left(\frac{a^2+b^2-c^2}{2ab}\right)\]

Une application numérique me donne ainsi $\gamma \approx 85.24^\circ$

Connaissant la largeur $e = 65$ cm du plan de travail, il est ensuite facile d’obtenir le décalage $h$ en cm par rapport à une coupe à angle droit :

\[h = \frac{e}{\textrm{tan} \gamma}\]

Vue schématique du plan de travail

Une application numérique nous donne finalement : $h \approx 5.4$ cm

En pratique, la coupe s’est révélée être plutôt bonne avec un écart maximal par rapport au mur inférieur à 5 mm ! Coup de bol ou robustesse de la méthode ? C’est l’enjeu de la section suivante.

Propagation des incertitudes

Incertitude sur les mesures de distance

Il est assez délicat d’estimer la précision de la mesure des longueurs du triangle fictif $ABC$. Les sources d’erreurs sont :

  • des longueurs mesurées pas exactement par rapport à l’horizontale (donc introduction d’un biais positif sur les longueurs)
  • une difficulté à mesurer la longueur $c$ par rapport à $a$ et $b$ où le mètre pouvait être plaqué sur le mur. Pour $c$ il est possible que le mètre ait un peu fléchi (donc à nouveau, introduction d’un biais positif sur $c$)
  • des murs pas tout à fait droits par rapport au fil à plomb
  • une incertitude sur la lecture de la mesure donnée par le mètre

Au final, j’ai grossièrement modélisé l’incertitude sur les trois longueurs par une loi normale centrée et d’écart-type $\sigma = 0.5$ cm. J’estime ainsi qu’il y a 95 % de chances que mon erreur soit inférieure au cm (intervalle de confiance à 2 sigma) et 68 % de chances que mon erreur soit inférieure au demi cm (intervalle de confiance à 1 sigma). Je fais l’hypothèse que mes trois mesures $(a,b,c)$ suivent la même loi (pas de différence donc entre $c$ d’une part et $a$ et $b$ d’autre part), que ces mesures sont indépendantes et qu’il n’y a aucun biais (loi normale centrée).

Incertitude sur le calcul de l’angle $\gamma$

La question est de savoir comment l’incertitude sur mes longueurs va se propager sur l’estimation de l’angle $\gamma$ et enfin sur la mesure du décalage $h$.

Dans l’hypothèse de petites perturbations par rapport aux longueurs vraies $(a_0, b_0, c_0)$, nous savons que $\gamma$ suivra une distribution gaussienne de moyenne $\gamma_0 = \gamma(a_0, b_0, c_0)$ (aucun biais) et d’écart-type $\sigma_\gamma$ à déterminer.

En appliquant le théorème de Taylor à la fonction $\gamma$ et en négligeant les termes d’ordre supérieur à 1, nous avons par ailleurs :

\[\begin{align} \gamma(\textcolor{red}{a_0+\varepsilon},b_0,c_0) &\approx \gamma(a_0, b_0, c_0) + \frac{\partial \gamma}{\partial a}(a_0, b_0, c_0) \cdot \varepsilon\\ \gamma(a_0,\textcolor{red}{b_0+\varepsilon},c_0) &\approx \gamma(a_0, b_0, c_0) + \frac{\partial \gamma}{\partial b}(a_0, b_0, c_0) \cdot \varepsilon\\ \gamma(a_0,b_0,\textcolor{red}{c_0+\varepsilon}) &\approx \gamma(a_0, b_0, c_0) + \frac{\partial \gamma}{\partial c}(a_0, b_0, c_0) \cdot \varepsilon \end{align}\]

Le calcul des dérivées partielles ne pose pas de problème, on rappelle simplement que $\textrm{arccos}’(x) = -1/\sqrt{1-x^2}$.

En nous rappelant que les mesures sont indépendantes, ceci nous permet d’établir :

\[\sigma_\gamma = \sigma \frac{180}{\pi} \sqrt{ \sum_{k = (a,b,c)}\left(\frac{\partial \gamma}{\partial k}(a_0, b_0, c_0)\right)^2}\]

Une application numérique nous donne alors : $\sigma_\gamma \approx 0.29^\circ$

Nous avons ainsi 95 % de chances que l’erreur sur l’angle $\gamma$ soit inférieure à $0.6^\circ$ (intervalle de confiance à 2 sigma) et 68 % de chances que cette erreur soit inférieure à $0.3^\circ$ (intervalle de confiance à 1 sigma).

Incertitude sur le calcul du décalage $h$

La propagation de l’incertitude sur la valeur de $h$ (et donc sur l’écart maximal qu’on peut observer sur la découpe) s’écrit finalement :

\[\sigma_h = \sigma_\gamma \frac{\pi}{180} e \left( 1 + \frac{1}{\tan \gamma_0}\right)\]

Une application numérique donne finalement : $\sigma_h \approx 0.33$ cm

Nous avons ainsi 99 % de chances que l’erreur sur le décalage $h$ soit inférieure au cm (intervalle de confiance à 3 sigma), 95 % de chances que cette erreur soit inférieure à 0.6 cm (intervalle de confiance à 2 sigma) et 68 % de chances que cette erreur soit inférieure à 0.3 cm (intervalle de confiance à 1 sigma).

A ceci doivent bien entendu s’ajouter les erreurs de tracé sur le plan de travail ainsi que l’erreur de découpe. Cette dernière est assez importante (l’épaisseur de la lame de la scie circulaire est du même ordre que $\sigma_h$).

Bilan des incertitudes

Les différents résultats que nous avons obtenus sont synthétisés dans le tableau ci-dessous.

Variable Moyenne Ecart-type
$a$ $a_0$ 0.5 cm
$b$ $b_0$ 0.5 cm
$c$ $c_0$ 0.5 cm
$\gamma$ $\gamma_0 = \gamma (a_0, b_0, c_0)$ $0.29^\circ$
$h$ $h_0 = e / \tan \gamma_0$ 0.33 cm

Vérification numérique

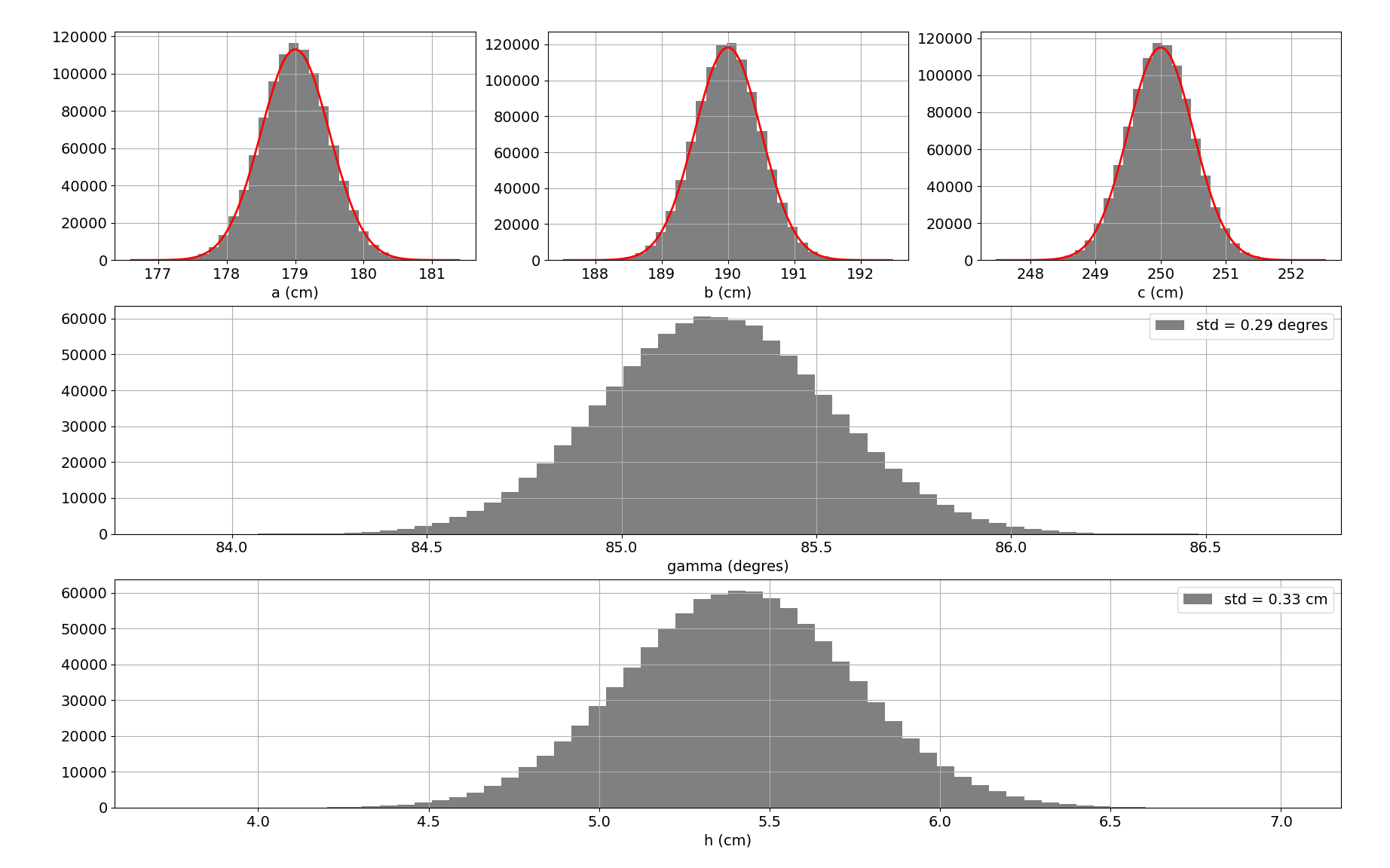
Afin de vérifier tout ceci, j’ai simulé un million de mesures des longueurs $(a,b,c)$ selon une loi normale de paramètres $(a_0, b_0, c_0)$ pour les moyennes et $(\sigma, \sigma, \sigma)$ pour les écarts-types. Ces distributions sont illustrées sur les trois histogrammes du haut (les courbes rouges représentent les gaussiennes attendues).

L’histogramme du milieu représente la dispersion des mesures de l’angle $\gamma$. On remarque que l’écart-type mesuré (0.29 degrés) est bien en adéquation avec l’écart-type théorique attendu !

Enfin, nous validons le même comportement pour l’estimation du décalage $h$ (histogramme du bas).

Etude statistique

Le code Python qui a généré ce graphique est le suivant (licence GPL tout ça).

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Sat Sep  4 19:18:28 2021

@author: donut
"""

from numpy import arccos, tan, pi, diff, linspace, sqrt, exp, std
from numpy.random import normal
from matplotlib import pyplot as plt, rc

fs = 14 # fontsize

rc('xtick', labelsize=fs) 
rc('ytick', labelsize=fs) 

a0 = 179 # cm
b0 = 190
c0 = 250
e  = 65

# a0=a0*10
# b0=b0*10
# c0=c0*10

m = 0; s = 0.5; # mean and std of gaussian noise
N = 10**6; # Number of samples

Nbins = 64;

# True values
gamma0 = arccos((a0*a0 + b0*b0 -c0*c0)/(2*a0*b0)) # rad
h0 = e/tan(gamma0) # cm


# Adding noise on (a,b,c) measurements

a = a0 + normal(m, s, N)
b = b0 + normal(m, s, N)
c = c0 + normal(m, s, N)

gamma = arccos((a*a + b*b -c*c)/(2*a*b)) # rad

h = e/tan(gamma)


# gamma function
def g(a,b,c):
    return arccos((a*a+b*b-c*c)/(2*a*b))

# First derivative of gamma function wrt a
def dg_da(a,b,c):
    x = (a*a+b*b-c*c)/(2*a*b)
    return 1/sqrt(1-x*x)*(x/a - 1/b)

# First derivative of gamma function wrt b
def dg_db(a,b,c):
    return dg_da(b,a,c)

# First derivative of gamma function wrt c
def dg_dc(a,b,c):
    x = (a*a+b*b-c*c)/(2*a*b)
    return 1/sqrt(1-x*x)*c/(a*b)


# Expected std of gamma at (a0, b0, c0)
la = abs(dg_da(a0,b0,c0))
lb = abs(dg_db(a0,b0,c0))
lc = abs(dg_dc(a0,b0,c0))

sg = s*180/pi*sqrt(la*la+lb*lb+lc*lc)

# Expected std of h at (a0, b0, c0)
sh = (1+1/(tan(gamma0)*tan(gamma0)))*e*sg*pi/180



plt.close('all')

plt.figure()

# Histogram for a
plt.subplot(3,3,1)
(n, bins, patches) = plt.hist(a, Nbins//2, color=[0.5,0.5,0.5])
dx = diff(bins)[0]
r = max([a0-bins[0], bins[-1]-a0])

A = N*2*dx/(s*sqrt(2*pi))*exp(-0.5)

x = linspace(a0-r,a0+r, num=100,endpoint=True)
y = A/(s*sqrt(2*pi))*exp(-0.5*(x-a0)/s*(x-a0)/s)

plt.plot(x,y, color='r', lw=2)
plt.xlabel('a (cm)', fontsize=fs)
plt.grid()


# Histogram for b
plt.subplot(3,3,2)
(n, bins, patches) = plt.hist(b, Nbins//2, color=[0.5,0.5,0.5])
dx = diff(bins)[0]
r = max([b0-bins[0], bins[-1]-b0])

A = N*2*dx/(s*sqrt(2*pi))*exp(-0.5)

x = linspace(b0-r,b0+r, num=100,endpoint=True)
y = A/(s*sqrt(2*pi))*exp(-0.5*(x-b0)/s*(x-b0)/s)

plt.plot(x,y, color='r', lw=2)
plt.xlabel('b (cm)', fontsize=fs)
plt.grid()


# Histogram for c
plt.subplot(3,3,3)
(n, bins, patches) = plt.hist(c, Nbins//2, color=[0.5,0.5,0.5])
dx = diff(bins)[0]
r = max([c0-bins[0], bins[-1]-c0])

A = N*2*dx/(s*sqrt(2*pi))*exp(-0.5)

x = linspace(c0-r,c0+r, num=100,endpoint=True)
y = A/(s*sqrt(2*pi))*exp(-0.5*(x-c0)/s*(x-c0)/s)

plt.plot(x,y, color='r', lw=2)
plt.xlabel('c (cm)', fontsize=fs)
plt.grid()

# Histogram for gamma
ax = plt.subplot(3,1,2)
(n, bins, patches) = plt.hist(gamma*180/pi, Nbins, color=[0.5,0.5,0.5], label='std = %3.2f degres' % std(gamma*180/pi))
plt.xlabel('gamma (degres)', fontsize=fs)
ax.legend(fontsize=fs)
plt.grid()

# Histogram for h
ax = plt.subplot(3,1,3)
plt.hist(h, Nbins, color=[0.5,0.5,0.5], label='std = %3.2f cm' % std(h))
plt.xlabel('h (cm)', fontsize=fs)
ax.legend(fontsize=fs)
plt.grid()

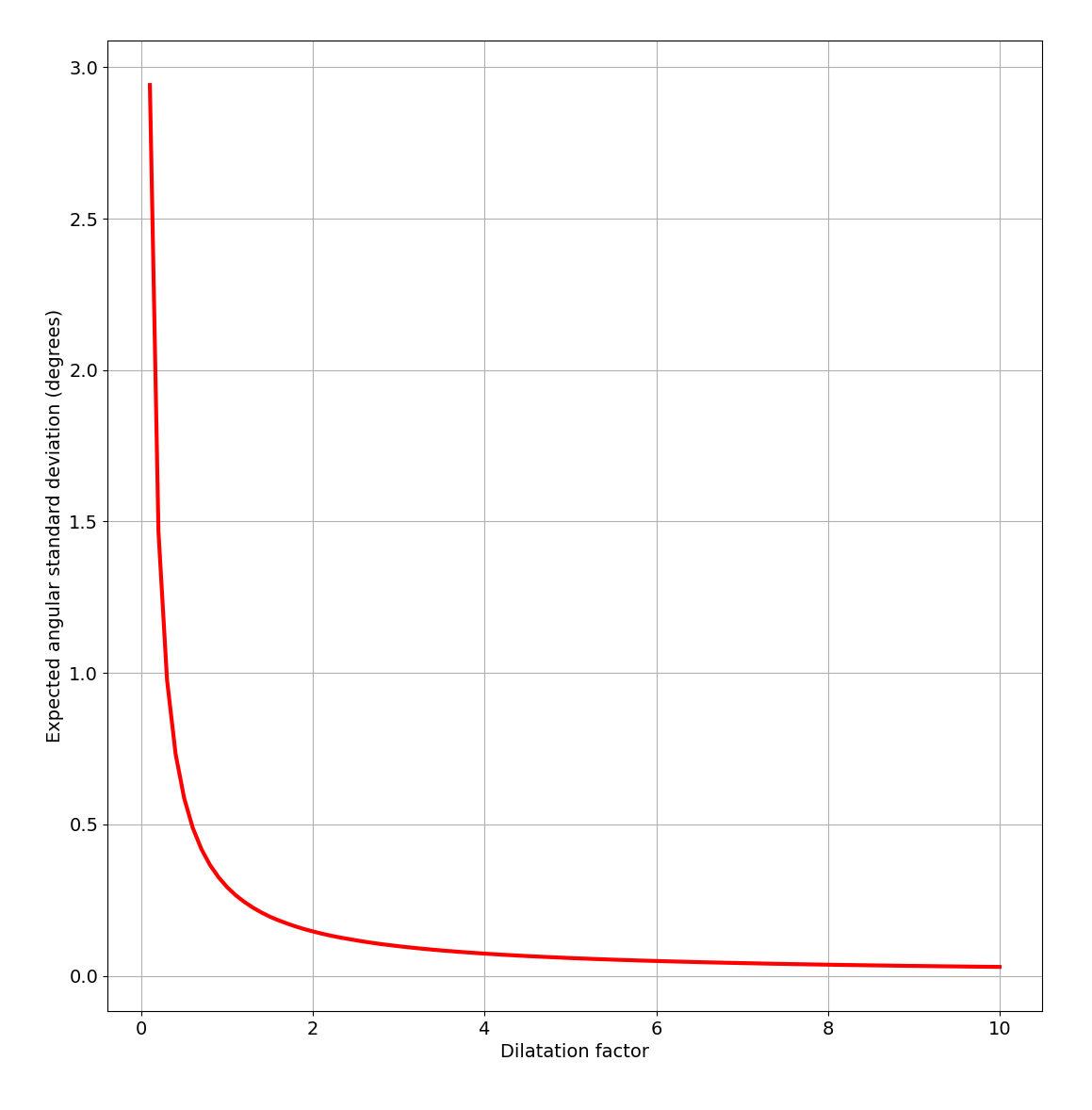
Influence de la taille initiale du triangle

Pour terminer, un petit mot sur l’importance de choisir un triangle $ABC$ le plus grand possible. La figure ci-dessous illustre l’évolution de l’écart-type attendu sur la mesure de l’angle $\gamma$ en fonction d’un facteur de dilatation des longueurs du triangle. Lorsque ce facteur est petit (par exemple 0.1) on considére un triangle plus petit que le triangle initial. On constate immédiatement que plus le triangle est grand (donc facteur de dilatation important), est meilleure sera la résolution de l’angle $\gamma$.

Influence de la taille du triangle