Et la pourriture pânée dit : « que la lumière soit »
« Il y a plus de choses dans un mot que de mots pour le dire. » Werner Lambersy
Soit $A$ un alphabet. A partir de cet alphabet, nous pouvons construire l’ensemble $\mathcal{M}$ des mots. Un mot est une suite finie d’éléments de $A$. On admettra ici que l’ensemble des mots est fini.
Nous définissons maintenant un livre comme étant une suite finie de mots. A la différence de l’ensemble des mots, l’ensemble des livres est infini dénombrable. Nous notons $\mathcal{L}$ cet ensemble.
Parmi tous ces livres, il existe une catégorie particulière que nous appelons dictionnaires et avec laquelle nous allons un peu nous amuser aujourd’hui. Attention, il y a beaucoup à en dire et c’est donc un long texte…
Ce qui différencie le dictionnaire des autres livres est qu’il est muni d’une structure. En effet, un dictionnaire $D$ est une suite finie de N définitions lexicales $\{(m_k, \sigma{}(m_k)\}$ avec $1 \leq k \leq N$.
Une définition lexicale est constituée de :
- une entrée $m_k$ : c’est un mot
- une définition $\sigma{}(m_k)$ : c’est une suite finie de mots
Par exemple, regardons un extrait de dictionnaire :
[LABARADOR] LE LABRADOR EST UN CHIEN SYMPATHIQUE
Ici l’entrée « LABRADOR » est définie par “LE LABRADOR EST UN CHIEN SYMPATHIQUE”. Cette définition se caractérise par sa longueur en nombre de mots $card(\sigma{}(m_k))$ qui vaut ici 6.
Donc un dictionnaire n’est défini que par l’ensemble de ses entrées $\Omega = \{m_k\}$ d’une part, et par l’application $\sigma$ d’autre part. On notera en pratique $D = (\Omega, \sigma)$.
Formellement, en notant $\mathcal{P}(X)$ l’ensemble des parties d’un ensemble $X$, nous définissons précisément $\Omega$ et $\sigma$ de la façon suivante :
\[\Omega \in \mathcal{P}(M)\] \[\begin{array}{ccccc} \sigma & : & \Omega &\to &\mathcal{L} \\ & & m_k &\mapsto & \sigma(m_k) \end{array}\]Réfléchissons un instant à ce que nous venons d’écrire. $m_k$ est un mot alors que $\sigma{}(m_k)$ est une suite finie de mots. Dans notre formalisme, $\sigma{}(m_k)$ est donc un livre.
Un dictionnaire est un livre qui, pour chaque mot donné d’un ensemble fini de mots, lui associe un livre. C’est très intrigant.
Nous notons $\mathcal{D}$ l’ensemble des dictionnaires. Nous allons explorer quelques unes des propriétés des dictionnaires.
Plan de l’article
- Plan de l’article
- Protocole
- Dictionnaires complets
- Dictionnaires normés
- Matrice de liaison, mots narcissiques et mots populaires
- Faisceaux entrant et sortant
- Mots inaccessibles
- Définition duale
- Mots dégénérés de rang k
- Poéticité
Protocole
Cet article a initialement été écrit le 23 juillet 2015 et se basait alors sur des codes que j’avais développé en Matlab. Ces codes un peu rudimentaires se basaient sur une version informatisée “brute” du Littré diffusée librement par François Gannaz et dont voici la référence :
Littré, Émile. Dictionnaire de la langue française. Paris, L. Hachette, 1873-1874. Electronic version created by François Gannaz. http://www.littre.org
Le passage du site sous Jekyll a été l’occasion d’un dépoussièrage de certains des articles donc celui que vous êtes actuellement en train de lire. Les modifications principales sont les suivantes :
- les codes ont été portés en Python et sont désormais accessibles en licence Creative Commons Attribution - Partage dans les mêmes conditions 3.0 non transposé sur Github
- les fonctions Python se basent désormais sur la version XML du Littré de François Gannaz qui est diffusée sous licence Creative Commons Attribution - Partage dans les mêmes conditions 3.0 non transposé. Ceci a deux conséquences :
- mes codes Pythons sont diffusés avec la même licence
- ceci peut avoir un léger impact sur les résultats présentés ici car il n’est pas garanti que nous ayons une bijection entre les deux dictionnaires
- les fonctions Python qui parsent les données XML sont beaucoup plus fines que leurs équivalents Matlab. Là où nous considérions auparavant de gros blobs de texte potentiellement mal structurés; nous sommes désormais beaucoup plus regardant en la qualité des mots. Par ailleurs nous nous bornons désormais à la stricte définition des mots (les champs “variante” dans les fichiers XML) et excluons de facto toutes les extentions (par exemple, les éthymologies). Ce choix est bien entendu discutable et a été motivé par des raisons de simplification.
- de la même façon, dans certains algorithmes nous excluons les répétitions de mot. De fait, la longueur des définions présentée ici est celle sans compter les répétitions. Ainsi la définion “UN RAT EST UN MAMMIFERE” a une longueur de 4 et non 5. Là encore ce choix est discutable.
Néanmoins, il est apparu que si ces choix ont eu un impact sur le contenu de la matrice de liaison, les principaux résultats macroscopiques que nous présentons demeurent eux inchangés1.
Avec notre nouveau code, nous dénombrons par exemple 75 638 entrées (c’est ce qu’on appelle la taille $N$ du dictionnaire). Auparavant nous en avions 78 427.
Dictionnaires complets
Un dictionnaire $D$ est dit complet si et seulement si tous les mots $x$ qu’il contient sont également les entrées d’une définition lexicale. Dans l’exemple précédent, notre dictionnaire est potentiellement complet si les mots “LE”, “EST”, “UN”, “CHIEN” et “SYMPATHIQUE” sont également des entrées. Formellement, nous écrivons :
\[\forall m \in \Omega,\quad \sigma(m) \in \mathcal{P}(\Omega)\]La plupart des dictionnaires ne sont pas complet car certains mots peuvent exister sous différentes formes (par exemple les différentes déclinaisons des conjugaisons) ou alors le nom d’un auteur peut apparaître dans une citation. Dans la suite de cette étude, nous nous restreignons aux dictionnaires complets.
Dictionnaires normés
Un dictionnaire est dit normé si et seulement si chacune des définitions a le même nombre de mots, c’est-à-dire :
\[\exists\, C \in \mathbb{N} \quad/\quad \forall m \in \Omega,\quad card(\sigma(m)) = C\]On appelle ordre d’un dictionnaire normé la valeur de C. Par exemple, dans un dictionnaire normé d’ordre 3, chaque entrée sera définie par exactement 3 mots.
Ainsi les deux définitions lexicales suivantes seraient envisageables :
[CHIEN] “MAMMIFÈRE”, “DOMESTIQUE”, “FIDÈLE”
[CHAT] “MAMMIFÈRE”, “DOMESTIQUE”, “INDÉPENDANT”
En pratique, les dictionnaires sont rarement normés et je pense même qu’actuellement il n’en existe aucun exemple dans le monde. Le cas du Littré, illustré dans la figure ci-dessous, est édifiant : les entrées sont définies en un seul mot pour les plus courts et jusqu’à plus de 1 500 mots pour les plus longs ! Nous ne sommes clairement pas dans le cas d’un dictionnaire normé… En moyenne les mots du Littré sont définis en 31 mots.
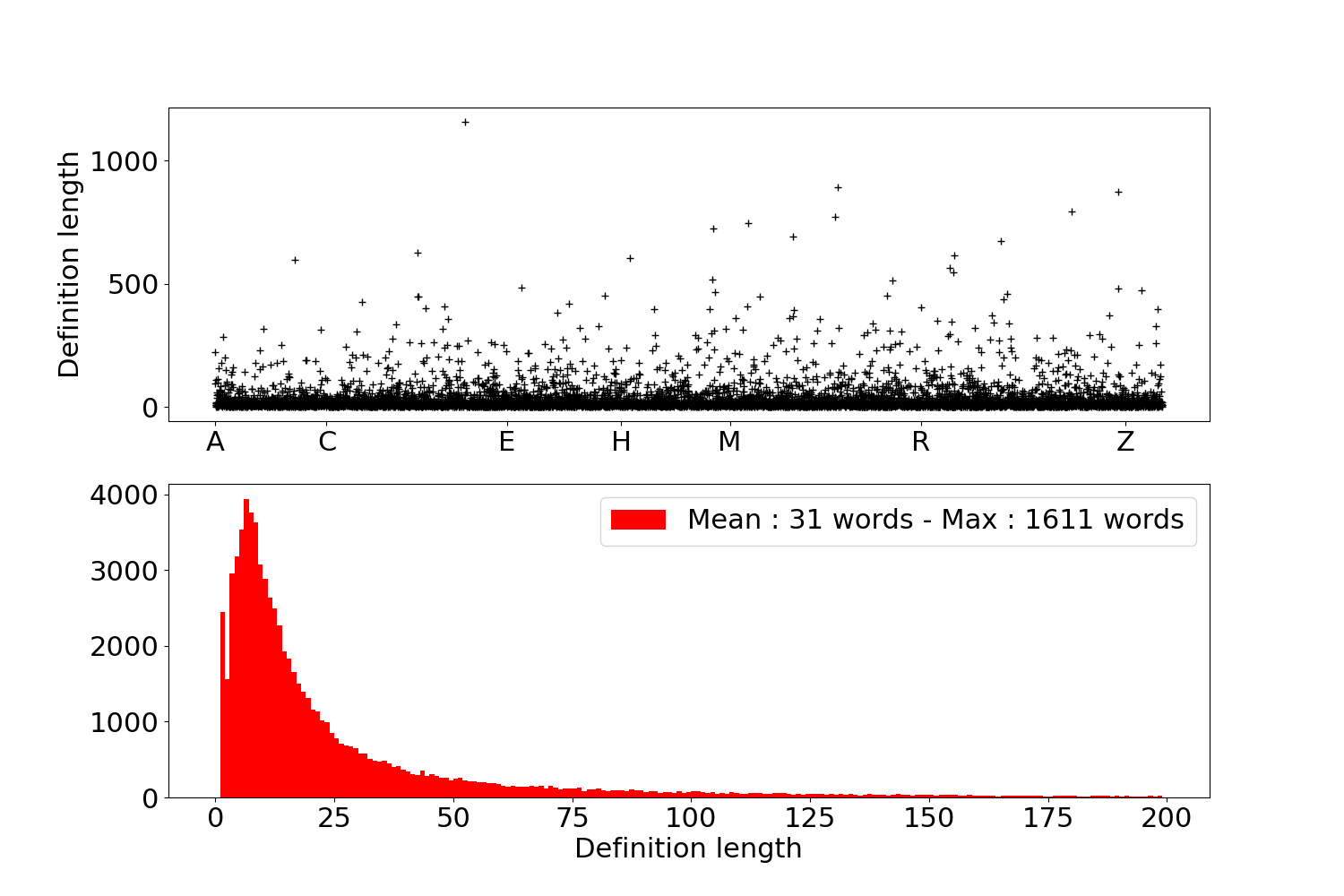
Les dix mots du Littré ayant la plus longue définition sont :
| Mot | Définition en nombre de mots |
|---|---|
| PRENDRE | 1611 |
| MAIN | 1422 |
| FAIRE | 1422 |
| TENIR | 1405 |
| PASSER | 1359 |
| TÊTE | 1296 |
| TIRER | 1269 |
| OEIL | 1244 |
| DE | 1196 |
| DONNER | 1158 |
Les mots ayant les définitions les plus courtes sont en général les renvois, ainsi que l’illustre l’exemple ci-dessous :
[FERRATIER] FERRETIER
Pour quelle(s) raison(s) un mot donné $m_1$ serait-il défini avec plus de mots qu’un autre mot $m_2$ ? Il faut chercher cette raison à l’extérieur de l’espace clôt des mots : si le mot $m_1$ pointe vers une réalité plus complexe ou plus générale que le mot $m_2$ alors il aura tendance à être défini en plus de mots. C’est ainsi que dans le Littré, le mot « MÉTIER » est défini en 392 mots alors que le mot « BOULANGER » n’est défini que par seulement 73 mots. En effet, « BOULANGER » est relativement simple à définir du moment qu’on fait référence au mot « MÉTIER » : la concision apparente de la définition de « BOULANGER » est ainsi masquée derrière la complexité du mot « MÉTIER ».
Résumons-nous :
- s’il existe des mots qui pointent vers une réalité proche de la réalité pointée par le mot que je cherche à définir, alors ma définition aura tendance à être courte : l’idée derrière « BOULANGER » se réduit aux idées derrière « MÉTIER et « PAIN ».
- dans le cas contraire, et pour combler l’absence de mots dans le voisinage de mon mot, je suis amené à partir de mots plus lointains pour arriver à ma définition : la longueur de ma description augmente.
Autrement dit, la longueur de la définition d’un mot donné pourra traduire la densité de mots au voisinage de la réalité pointée par mon mot. La densité maximale se rencontrera dans le cas des synonymes : deux mots différents pointeront vers la même réalité. La densité minimale se rencontrera au voisinage des mots qu’on appellera primordiaux faute d’un meilleur terme. Pour le Littré, « FAIRE », « MAIN » et « TENIR » sont ainsi primordiaux.
Donc au final, les dictionnaires sont rarement normés du fait de l’inhomogénéité de la répartition des mots dans la réalité perceptible. Si nous tenions malgré tout à avoir un dictionnaire normé d’ordre 3, il nous faudrait donc introduire de nouveaux mots intermédiaires pour régulariser la couverture du monde. De même que « BOULANGER » repose sur « MÉTIER » pour gagner en concision, « MÉTIER » devra lui-même reposer sur un autre mot, potentiellement à inventer, pour raccourcir sa définition.
Si nous tenions en même temps à garder un dictionnaire complet (c’est-à-dire que chaque nouveau mot nouvellement créé soit également défini en trois mots) alors on s’aperçoit qu’il nous faudrait un nombre infini de mots pour décrire les mots. Et je repense maintenant à ce que disait Werner Lambersy : « Il y a plus de choses dans un mot que de mots pour le dire ».
Remarquons toutefois qu’il existe des cas triviaux de dictionnaire complet et normé. Ainsi, si on choisit $\forall m \in \Omega, \sigma(m) = m$, les mots seraient définis par eux-mêmes ce qui donnerait :
[CHIEN] CHIEN
[CHAT] CHAT
[BOULANGER] BOULANGER
[MÉTIER] MÉTIER
Bien qu’en théorie parfaitement structuré, complet et normé d’ordre 1, un tel dictionnaire rencontrerait je pense un cuisant échec commercial…
Arrivé à ce stade, nous devons apporter une clarification importante : un dictionnaire ne définit absolument pas la réalité derrière les mots. En effet à l’aide d’un dictionnaire au sens où nous l’avons défini, je serai bien incapable de définir la réalité qui se cache derrière le mot « LABRADOR ». En revanche, ce dictionnaire me permet de souligner les relations que les mots entretiennent entre eux et ce sont deux choses totalement séparées. Ici, je sais juste que le mot « LABRADOR » est lié aux mots « CHIEN » et « SYMPATHIQUE ».
Matrice de liaison, mots narcissiques et mots populaires
Afin de mettre en évidence les relations que les mots entretiennent entre eux, on définit la matrice $M_{i,j}$ par :
\[\begin{array}{cccl} M(i,j) & = & 1 & si \; m_j \in \sigma(m_i)\\ & & 0 & sinon \end{array}\]Autrement dit, $M_{i,j} = 1$ si le mot $m_j$ appartient à la définition du mot $m_i$ et $M_{i,j} = 0$ dans tous les autres cas.
Représenter cette matrice par une image est compliqué. En effet, elle est de taille 78 427 pixels par 78 427, ce qui fait un peu plus de 6 milliards de points (un nombre comparable à la population mondiale…). Il faudrait près de 700 écrans 4K mis côte-à-côte pour pouvoir l’afficher en intégralité…
Le code Matlab utilisait des moyennes sur des boîtes de 400 mots proches pour estimer l’allure de cette matrice. Désormais, nous nous contentons uniquement de décimer les lignes et colonnes d’un facteur 5.

Ici un pixel clair (blanc) signifie que $M(i,j)$ vaut 1 : les mots se citent entre eux. Au contraire, un pixel sombre (noir) signifiera que les mots ont peu de lien entre eux au sens du dictionnaire.
Cette image a trois faits remarquables :
- elle est globalement sombre : les mots sont peu liés entre eux,
- on note la présence d’une diagonale claire,
- enfin il y a un certain nombre de lignes verticales claires.
La présence d’une diagonale claire traduit la tendance des mots à se citer eux-mêmes dans leur définition. C’était par exemple le cas de notre définition de « LABRADOR » en début de texte. Nous appelons de tels mots des mots narcissiques. Un mot sera d’autant plus narcissique qu’il se citera souvent dans sa définition. Environ 44% des mots du Littré sont narcissiques. Les premiers d’entre eux sont donnés ci-dessous, on remarque que les mots aux plus longues définitions sont logiquement ceux qui sont les plus susceptibles de s’auto-citer. Etre primordial, c’est être narcissique.
| Mot | Auto-citations |
|---|---|
| DE | 693 |
| MAIN | 614 |
| A | 476 |
| TÊTE | 468 |
| TEMPS | 464 |
| PAS | 417 |
| QUE | 415 |
| TOUT | 405 |
| FAIRE | 371 |
| FEU | 369 |
Les lignes verticales claires quant à elles sont dues à des mots qu’on qualifiera de populaires et qui sont fréquemment cités dans la définitions des autres mots. Sans grande surprise, on voit surgir les mots qui structurent notre langue (« DE », « ET », « LE », « UN » etc…). C’est à ce niveau que le mot « ÉTYMOLOGIE » sortait car il revenait dans la plupart des définions, il est désormais absent (voir section “Protocole” au début de l’article).
| Mot | Rang | Nombre de mots qui le cite |
|---|---|---|
| DE | 1 | 56489 |
| QUI | 2 | 38263 |
| LA | 3 | 35790 |
| DES | 4 | 30766 |
| ET | 5 | 30232 |
| A | 6 | 29894 |
| LES | 7 | 29436 |
| LE | 8 | 28810 |
| TERME | 9 | 26769 |
| EN | 10 | 23332 |
Parmi cette liste de mots populaires, il y a des mots populaires non-triviaux qui apparaissent à partir du rang 60 environ. En voici quelques exemples.
| Mot | Rang | Nombre de mots qui le cite |
|---|---|---|
| ACTION | 61 | 4998 |
| HOMME | 62 | 4940 |
| GRAND | 68 | 4107 |
| CORPS | 70 | 3966 |
| TEMPS | 75 | 3796 |
| BOTANIQUE | 90 | 3179 |
Quoiqu’il en soit, après avoir remarqué les premières propriétés de la matrice $M$, je vous propose de continuer notre petite exploration.
Faisceaux entrant et sortant
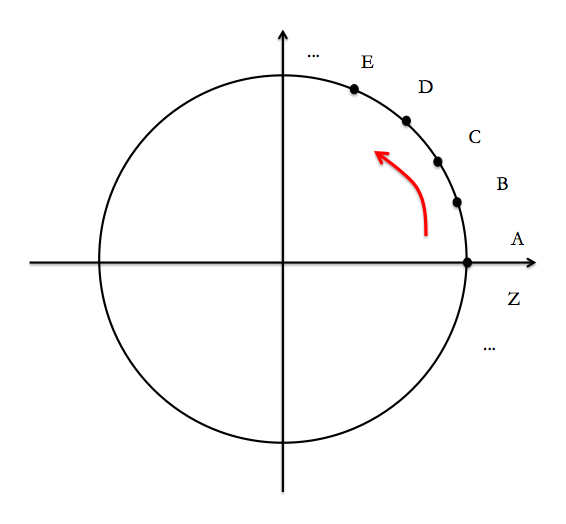
Pour représenter les liaisons que les mots entretiennent, nous allons disposer les mots le long d’un cercle par ordre alphabétique croissant ainsi que l’illustre la figure ci-dessous.
Choisissons un mot au hasard sur ce cercle, par exemple « CANARD ». Nous pouvons tout d’abord relier par un trait tous les mots cités dans la définition de « CANARD » avec « CANARD » lui-même, nous obtenons alors ce que nous appelons le faisceau sortant de « CANARD » (voir ci-dessous).

De la même façon, nous pouvons maintenant relier le mot « CANARD » avec tous les mots qui le citent dans leur définition. Nous appelons une telle figure le faisceau entrant de « CANARD » (voir ci-dessous également).
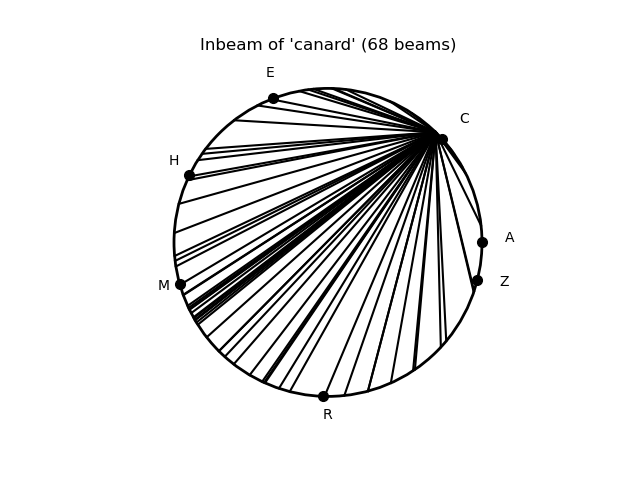
Parmi les éléments du faisceau entrant de « CANARD », nous trouvons par exemple « PALMIPÈDE », « CANETON », « CANARDIÈRE », « OIE »… mais aussi d’autres curiosités comme « CURÉ » ou « FACTEUR ».
[CURÉ] (…) MONSIEUR LE CURÉ N’AIME PAS LES OS, QUE LUI DONNEZ-VOUS À MANGER ? JEU D’ENFANTS OU ATTRAPE FONDÉE SUR L’HOMOPHONIE D’OS ET DE LA VOYELLE O. IL FAUT RÉPONDRE PAR UN MOT DANS LE NOM DUQUEL LA VOYELLE O N’ENTRE PAS : DES NAVETS, DU VEAU, UN CANARD, ETC. MAIS SI L’ON DIT DES CAROTTES, DES ABRICOTS, ETC. ON DONNE UN GAGE. (…)
Quoiqu’il en soit, faisceau entrant $FE(m_i)$ et faisceau sortant $FS(m_i)$ sont définis par les équations suivantes :
\[FS(m_i) = \sigma ( m_i)\] \[FE(m_i) = \{ m_j \in \Omega \;/\; m_i \in \sigma ( m_j) \}\]Nous notons $n_{FS}(m_i)$ (respectivement $n_{FE}(m_i)$) le cardinal de l’ensemble $FS(m_i)$ (respectivement de $FE(m_i)$). $n_{FS}(m_i)$ représente simplement la longueur de la définition du mot $m_i$ alors que $n_{FE}(m_i)$ représente sa popularité.
Si nous traçons l’une en fonction de l’autre nous obtenons la courbe ci-dessous (en échelle logarithmique). L’axe des abscisse représente la longueur des mots et l’axe des ordonnées leur popularité. Nous voyons que les mots les mieux définis ont ainsi tendance à être les plus cités. Le cas particulier du mot « CANARD » est représenté ici par une croix rouge.
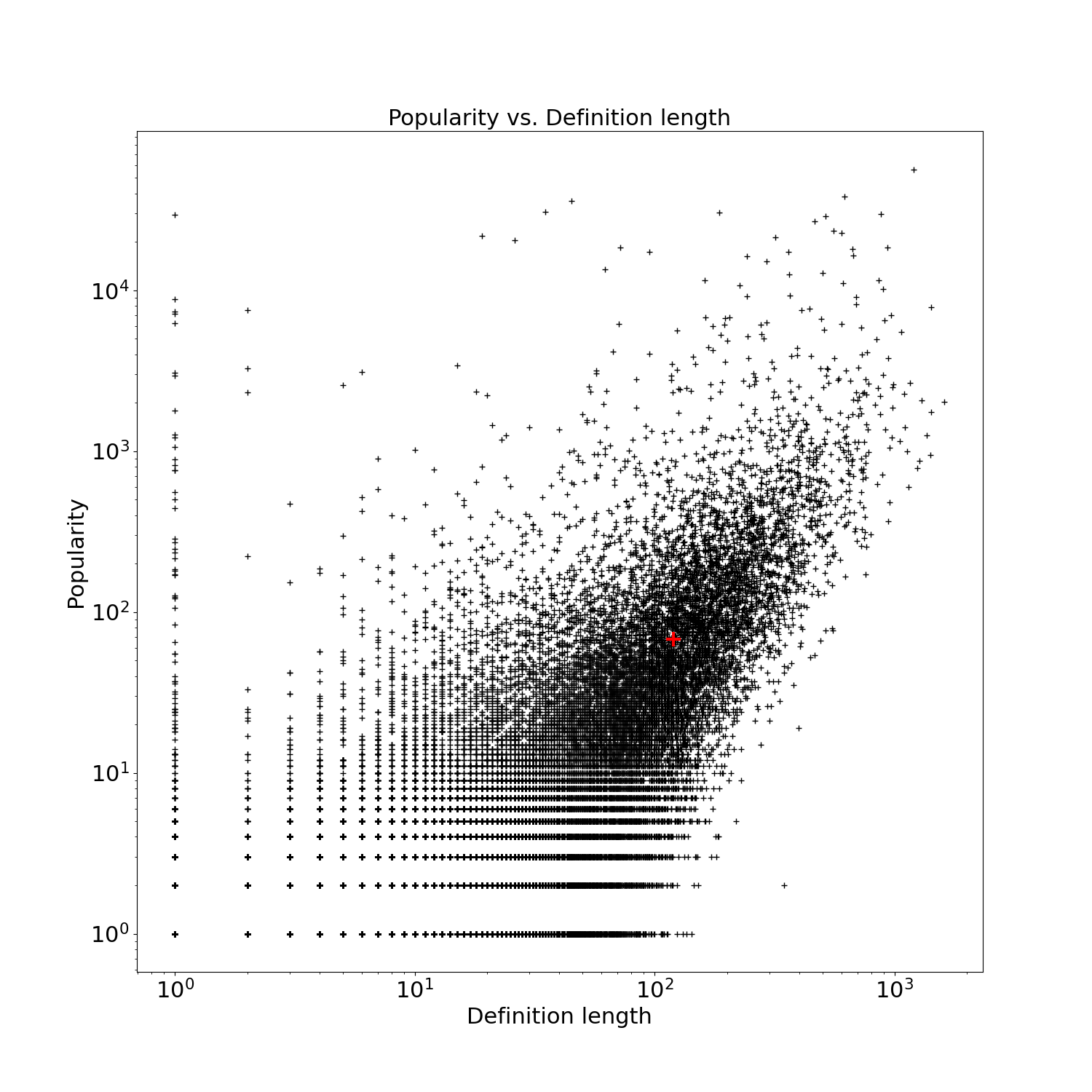
Sur ce graphique, on pourrait imaginer de partitionner l’ensemble des mots selon qu’ils sont placés au-dessus ou au-dessous de la diagonale $nFS=nFE$. Dans le premier cas, ils sont plus populaires que primordiaux. Dans le second cas, ils sont plus primordiaux que populaires. On pourrait appeler mot parfait un mot pour lequel sa primordialité est égale à sa popularité; c’est-à-dire un mot qui serait défini en autant de mots qu’il n’y a de mots dans le dictionnaire qui le citent. Je ne sais pas si c’est une piste intéressante à creuser.
Mots inaccessibles
Un mot $m_j$ est dit inaccessible s’il n’apparaît dans la définition d’aucun autre mot. Ceci s’écrit indifféremment :
\[\forall m_i \in \Omega\;, m_j \notin \sigma (m_i)\] \[\forall i \in [1, N]\;,\; M(i,j) = 0\]Près de 43% des mots du Littré sont inaccessibles. En voici quelques exemples :
- « ASSERTORIQUE »
- « BUHOTIER »
- « CRICETIN »
- « EMPOTÉ, ÉE »
- « GNATHODONTE »
- « LAMPROYON »
- « OPHTHALMOXYSE »
- « SPOULINER »
- « ZYTHOGALE »
Définition duale
La définition d’un mot $m_i$ est l’ensemble $\sigma (m_i)$ des mots de sa définition : c’est son faisceau sortant. Réciproquement, la définition duale d’un mot $m_i$ est l’ensemble des mots qui le citent dans leur définition. Ce n’est rien d’autre que le faisceau entrant de $m_i$ que nous avons évoqué tantôt. Notons que seuls les mots accessibles admettent une définition duale.
Prenons l’exemple du mot TUER :
- Le mot TUER apparaît 44 fois dans la définition du mot TUER
- Le mot TUER apparaît 4 fois dans la définition du mot ASSASSIN
- Le mot TUER apparaît 4 fois dans la définition du mot CHIEN, CHIENNE
- Le mot TUER apparaît 4 fois dans la définition du mot DONNER
- Le mot TUER apparaît 3 fois dans la définition du mot AFFAIRE
- Le mot TUER apparaît 3 fois dans la définition du mot COUVRIR
- Le mot TUER apparaît 3 fois dans la définition du mot ESCOFFIER
- Le mot TUER apparaît 3 fois dans la définition du mot LAVER
- Le mot TUER apparaît 3 fois dans la définition du mot MEURTRIR
- Le mot TUER apparaît 3 fois dans la définition du mot OCCIRE
- etc…
La définition duale d’ordre 3 de « TUER » serait donc, selon le Littré :
[TUER] TUER ASSASSIN CHIEN, CHIENNE.
Voici quelques autres exemples, ci-dessous.
[DIEU] DIEU GRÂCE DE GARDER MAIN HOMME CROIX ŒIL PLAIRE VOIR TOUTE GLOIRE SAINT MERCI VUE…
[AMOUR] AMOUR PRENDRE RETOUR DE TOUT FEU JOUR SOUTENIR AMOUREUX FAIRE…
[POÉSIE] POÉSIE MUSE PROSE LYRIQUE HÉROÏQUE POÉTIQUE BERGERIE CHANT CONTEXTURE EXPOSITIF FLEUVE GUITARE HAUTBOIS JEU LÉGER
Il est amusant de voir le sens premier se diluer (?) au fur et à mesure. Ainsi les mots « CHIEN » et « DONNER » apparaissent dans la définition duale de « TUER »…
Mots dégénérés de rang k
Un mot est dit dégénéré si on doit faire appel à lui pour le définir.
Partez d’un mot quelconque $m_i$ et regardez sa définition dans le dictionnaire. Si le mot $m_i$ apparaît dans sa définition, vous êtes dans un cercle vicieux : pour définir $m_i$, vous avez besoin de définir $m_i$. De tels mots sont dit dégénérés de rang 0, ce sont exactement les mots narcissiques que nous avons rencontrés tout à l’heure. Dans l’Univers des mots, les narcissiques sont des dégénérés…
Si $m_i$ n’apparaît pas dans sa définition, nous ne sommes pas tirés d’affaire pour autant. En effet, nous aurions peut-être besoin de définir un des mots de la définition de $m_i$. Et il se peut que $m_i$ apparaisse dans une de ces définitions ! De tels mots sont appelés mots dégénérés de rang 1.
Nous pouvons procéder itérativement pour définir les mots dégénérés de rang k. Une définition formelle d’un mot dégénéré de rang k est donnée ci-dessous :
\[m_i \in\; \stackrel{\sim}{\sigma}^k (m_i)\]La fonction $\stackrel{\sim}{\sigma}$ est une généralisation de la fonction $\sigma$, l’ensemble de départ n’est plus l’ensemble des mots $\Omega$ mais l’ensemble des livres : ceci nous permet de définir les composées successives $\stackrel{\sim}{\sigma}^k$.
\[\begin{array}{ccccl}\stackrel{\sim}{\sigma} & : & \mathcal{L} & \to & \mathcal{L}\\& & \lambda & \mapsto & \bigcup_{m_k \in \lambda}\; \sigma (m_k)\end{array}\]On appelle dégénérescence d’un dictionnaire D, le rang minimal $k_0$ à partir duquel tous les mots sont dégénérés.
Nous pouvons être encore plus drastique en considérant comme dégénéré tout mot dégénéré par lui-même ou citant un mot dégénéré. En ce sens, tout dictionnaire complet est d’une façon ou d’une autre dégénéré au bout d’un certain temps. Le dictionnaire construit du sens sur des bases bancales et indéfinies, sur du sable en somme.
Poéticité
Poéticité terme-à-terme
Nous arrivons maintenant à la fin de cette petite analyse et nous allons tenter de définir un estimateur de la poéticité entre deux mots donnés, au sens du Littré.
Selon quels critères, une association de deux mots sera-t-elle considérée comme poétique ? Umberto Eco dans son Oeuvre Ouverte fait reposer cette notion sur la notion d’ambiguïté : une association sera d’autant plus poétique qu’elle sera ambiguë. Un homme qui, à l’entrée de sa propriété, mettrait l’écriteau « ATTENTION CHIEN MÉCHANT » n’incitera que modestement les éventuels badauds à s’abandonner à la médiation et la rêverie. En revanche, le panneau « ATTENTION CHIEN INFINI » ou « ATTENTION CHIEN CREUX » sera tout de suite beaucoup plus intrigant. Les mots « CHIEN » et « MÉCHANT » entretiennent entre eux des relations beaucoup plus étroites que « CHIEN » et « INFINI » ou « CHIEN » et « CREUX ».
Les notions de faisceaux entrant et sortant nous permettent d’estimer grossièrement ce degré de proximité qui relie les mots. Par exemple, si deux mots partagent beaucoup de mots communs dans leur définition respective alors on pourra les considérer comme proches. Ainsi « CHAT » et « CHIEN » feront vraisemblablement apparaître les mots « MAMMIFÈRE », « DOMESTIQUE », « COMPAGNON » etc… dans leur définition : ils sont proches. Réciproquement, les définitions de « CHIEN » et de « PARPAING » ne partageant a priori que peu de mots en commun, on pourra les considérer comme éloignés. Mathématiquement ceci se traduira par la taille d’ensemble de l’intersection des faisceaux sortants $FS_1$ et $FS_2$, ainsi que l’illustre la figure ci-dessous.
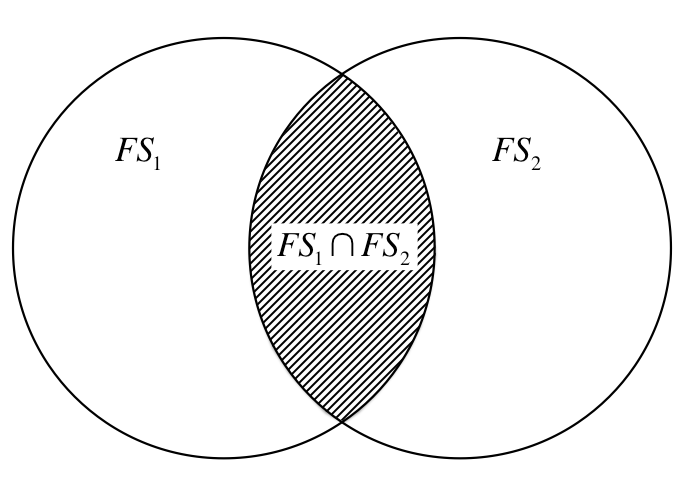
Mais nous ne devons pas oublier que le Littré n’est pas normé : deux mots ayant des longues définitions seront ainsi plus susceptibles d’être proche que deux mots aux définitions laconiques. Il faut donc normaliser la quantité précédente par la taille de l’union des deux définitions.
Pour terminer, il faut prendre en compte que les mots n’ont pas la même popularité : partager le mot « ET » dans deux définitions n’a pas la même signifiance que partager le mot « MAMMIFÈRE ». Idéalement, il faudrait pondérer chaque mot par sa popularité, mais je me contenterai d’ignorer les contributions des 50 mots les plus populaires. Nous obtenons au final une estimation de la proximité entre deux mots $m_1$ et $m_2$ :
\[p(m_1, m_2) = \frac{card(FS_1 \bigcap FS_2)}{card(FS_1 \bigcup FS_2)}\]Au final nous avons donc un estimateur du degré de proximité entre les mots. Quelles sont ses propriétés ? Cet estimateur est tout d’abord symétrique, puisque $\forall\; (m_1, m_2) \in \Omega^2\; p(m_1, m_2) = p(m_2, m_1)$. La « distance » qui sépare $m_1$ de $m_2$ est la même que la distance qui sépare $m_2$ de $m_1$. C’est heureux.
On peut ensuite montrer que cet estimateur est compris entre 0 et 1. Il vaut 1 si les deux mots partagent exactement les mêmes définitions. Ainsi les mots entretiennent avec eux-mêmes une proximité de 1 : $p(m,m) = 1$. Au contraire, cet estimateur vaut 0 si les définitions des mots ne partagent aucun mot en commun. Dans le cas général, nous avons donc :
\[0 \leq p(m_1, m_2) \leq 1\]Deux mots seront d’autant plus poétiques entre eux que leur proximité sera faible.
Ainsi, voici les premiers noms proches du mot « DIEU » : auriez-vous pu retrouver le mot DIEU en ne connaissant que ses plus proches mots ?
- DIEU : 100% de proximité avec DIEU
- REGARDER : 29.1% de proximité avec DIEU
- NATURE : 28.6% de proximité avec DIEU
- HOMME : 28.4% de proximité avec DIEU
- SAVOIR : 28.2% de proximité avec DIEU
- DIRE : 27.9% de proximité avec DIEU
- NOM : 27.8% de proximité avec DIEU
- COEUR : 27.8% de proximité avec DIEU
- MONDE : 27.7% de proximité avec DIEU
- PART : 27.6% de proximité avec DIEU
- MOURIR : 27.6% de proximité avec DIEU
- VOULOIR : 27.4% de proximité avec DIEU
- PARLER : 27.4% de proximité avec DIEU
- HEURE : 27.3% de proximité avec DIEU
- LIEU : 27.0% de proximité avec DIEU
- RIEN : 26.9% de proximité avec DIEU
- PAROLE : 26.9% de proximité avec DIEU
Il y a exactement 416 mots dont la définition ne partage aucun mot non triviaux avec la définition de DIEU (proximité nulle). La plupart d’entre-eux sont des renvois ou ont des définitions laconiques. Parmi ces 416 mots, les plus pertinents sont : PRIME-SAUT, ÉPITHÉTIQUE, PANÉ, POURRITURE.
Si nous demandons aux mots en question d’être défini avec un minimum de 150 mots (soit la valeur moyenne d’une définition) alors nous trouvons que les mots suivants entretiennent eux aussi des rapports assez distants avec DIEU (proximité entre 6 et 7 % pas plus) : MOLETTE, BATTE, PLATE-BANDE, RAYURE, CUVETTE, CULOT, HÉLICE, TYMPAN, GOUGE, FRAISE, FONDANT, CERF-VOLANT, AXE, ÉCLISSE, VELOUTÉ, TUBERCULE, SAVON, MITRAILLE, CHANFREIN, ÉQUATION, PROGRESSIF, TENSION, MÉTIS et ÉPAISSEUR.
Je ne sais pas ce qu’est précisément Dieu, mais d’après le Littré je n’ai pas beaucoup de chances de le trouver dans une usine…
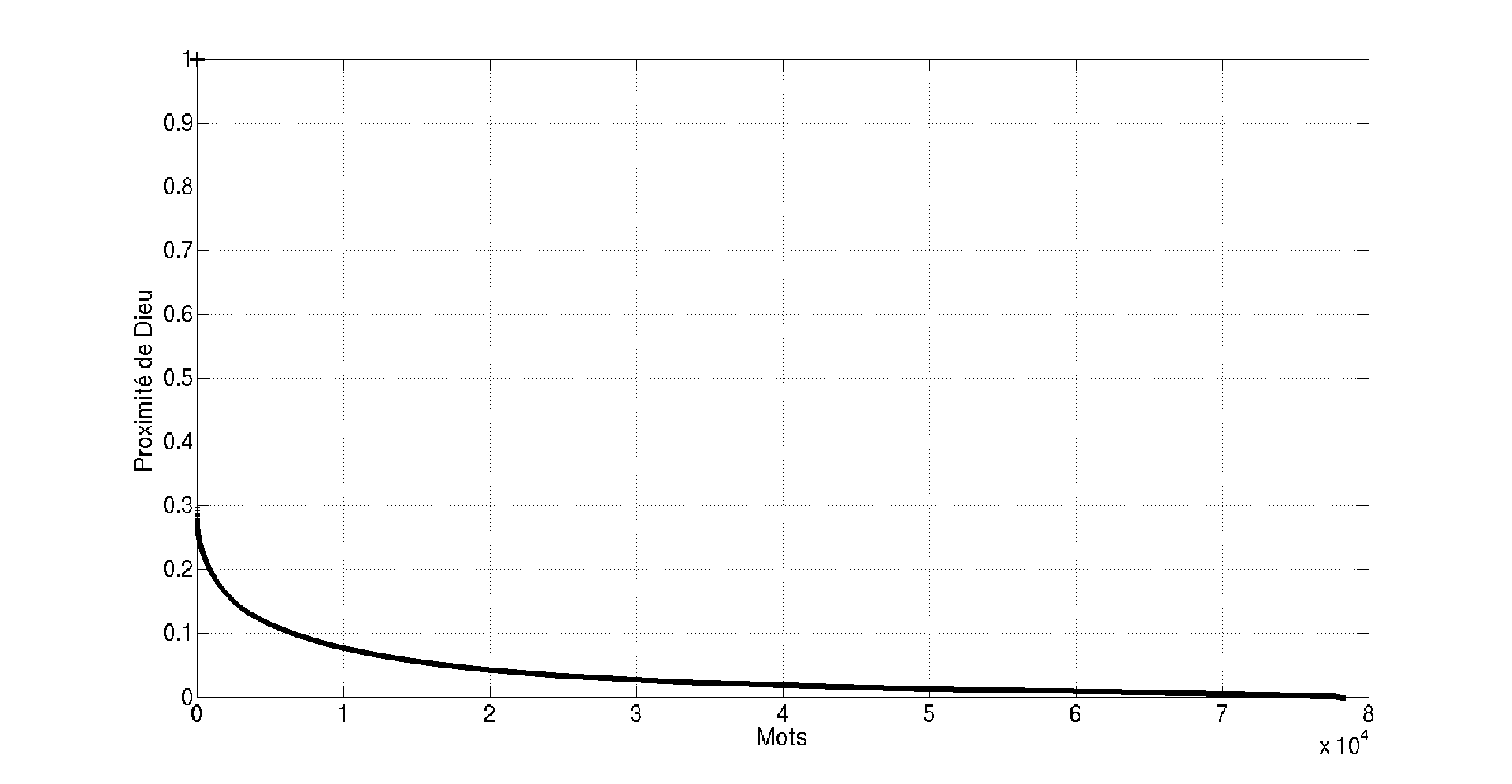
La figure ci-dessous illustre la décroissance de la proximité des mots à « DIEU ». Dieu occupe naturellement le point 0 et vaut 1. Nous tombons ensuite directement à 28% avec des mots tels que « NATURE », « HOMME » etc. Puis nous descendons tranquillement vers 0, petit bastion des mots poétiquement liés à « DIEU ».
Poéticité duale
Nous avons donc établi un premier moyen d’établir la proximité entre deux mots. Néanmoins, bien que cet estimateur est assez efficace, il reste perfectible. On voit sur l’image précédente que l’essentiel des mots ne sont que peu liés à « DIEU » : près de 80% des mots ont une proximité avec Dieu inférieure à 5%. Pourrions-nous améliorer cela ?
Nous serions ici tentés de définir la proximité duale $\bar{p}(m_1, m_2)$ par l’équation suivante :
\[\bar{p}(m_1, m_2) = \frac{card(FE_1 \bigcap FE_2)}{card(FE_1 \bigcup FE_2)}\]Auparavant, deux mots étaient proches s’ils citaient les mêmes mots. Maintenant deux mots sont dualement proches s’ils sont cités par les mêmes mots. Dans notre exemple initial, « CHIEN » et « CHAT » pourront être cités par les mots « ANIMAL », « RAGE », « PUCE », « CROQUETTE » etc.
Établir cette équation est d’une élégante symétrie, mais il ne faut pas oublier que les ensembles $FE_1$ et $FE_2$ sont potentiellement vides ! En effet, nous avons vu que cela survient dans les cas des mots inaccessibles qui ne sont cités par aucun autre mot. Dans un tel cas, la proximité duale de deux mots inaccessibles est une valeur indéterminée, potentiellement infinie. Au sens de la proximité duale, les mots inaccessibles sont donc des mots très poétiques. Par exemple, rappelez-vous que le premier mot inaccessible du Littré au sens alphabétique est le mot « ASSERTORIQUE » : imaginez la tête du badaud devant l’écriteau « ATTENTION CHIEN ASSERTORIQUE ». C’est un mot poétiquement passe-partout au sens du Littré.
[ASSERTORIQUE] (Philosophie) (Rare) Qui énonce une vérité de fait, sans la poser comme nécessaire.
Rechercher la poéticité dans les mots rares n’est pas nouveau. Nous laissons cela aux Parnassiens Contemporains et nous nous interdisons de notre côté de considérer la proximité duale de deux mots inaccessibles.
Voici au sens dual, les premiers mots proches de DIEU : auriez-vous pu retrouver le mot DIEU en ne connaissant que ses plus proches mots duaux ? L’exercice me semble plus difficile qu’auparavant…
| Proximité directe | Degré de proximité en % | Proximité duale | Degré de proximité duale en % |
|---|---|---|---|
| DIEU | 100 | DIEU | 100 |
| REGARDER | 29.1 | MON | 25.8 |
| NATURE | 28.6 | VOUS | 25.7 |
| HOMME | 28.4 | NOUS | 25.0 |
| SAVOIR | 28.2 | VOTRE | 24.7 |
| DIRE | 27.9 | LUI | 24.2 |
| NOM | 27.8 | MONDE | 22.7 |
| COEUR | 27.8 | HOMME | 22.6 |
| MONDE | 27.7 | AVOIR | 21.6 |
| PART | 27.6 | TOUJOURS | 21.6 |
| MOURIR | 27.6 | VIE | 21.6 |
| VOULOIR | 27.4 | MORT, MORTE | 21.3 |
| PARLER | 27.4 | COEUR | 21.0 |
| HEURE | 27.3 | ROI | 21.0 |
| LIEU | 27.0 | JAMAIS | 20.8 |
| RIEN | 26.9 | ETRE | 20.4 |
| PAROLE | 26.9 | GRAND, GRANDE | 20.0 |
De la même façon, les mots ayant une proximité duale nulle avec Dieu sont : SILICATE, SÉCRÉTION, DOCUMENT, GALLINACÉS, MANGANÈSE, IODE, EXCROISSANCE, BAQUET, BRÉE et VIRUS.
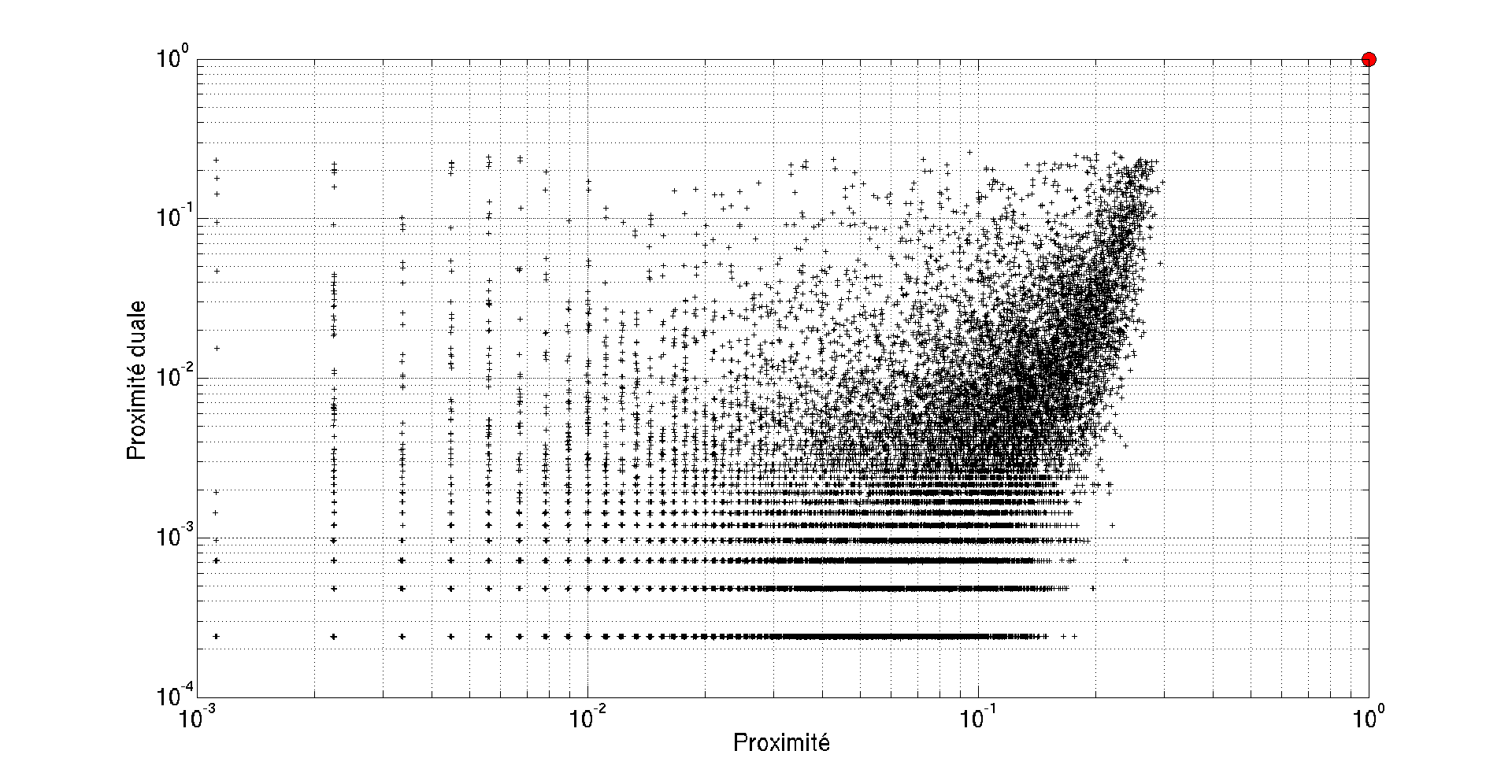
Proximité et proximité duale sont a priori décorrelées mais tracer l’une en fonction de l’autre permet de voir que deux mots proches dans leurs définitions auront tendance à être cités par les mêmes mots.
Dans la figure ci-dessous, Dieu est le seul mot qui maximise à la fois sa proximité et sa proximité duale. Il est représenté par un petit rond rouge. Plus on s’en éloigne, plus on gagne en poéticité.
Poéticité totale
On définit la proximité totale par :
\[P(m_1, m_2) = \sqrt{p^2(m_1,m_2) + \bar{p}^2(m_1,m_2)}\]Minimiser la proximité, c’est maximiser la poéticité. Grosso modo, la poéticité duale nous permettra d’affiner notre sélection.
Poétisation de ce qu’on trouve au dos des paquets de café
Voici ce qu’on apprend en lisant le dos d’une cartouche de capsules Nespresso « Dharkan » :
« Cet assemblage d’Arabicas d’Amérique Latine et d’Asie dévoile son caractère grâce à une torréfaction longue à basse température. Sa puissante personnalité révèle des notes torréfiées intenses ainsi que des touches de céréales grillées et cacao amer s’exprimant dans une texture veloutée et soyeuse. »
En passant à la moulinette ce petit texte, nous obtenons alors une définition poétisée du café « Dharkan » :
« Ce PREMIER-NÉ d’Amérique Latine et d’Asie dévoile ses SPASMES grâce à une AUTOPSIE longue à bas CHAGRIN. Sa RÉTROACTIVE FAÏENCE révèle des BÉNÉVOLES FLEGMATIQUES ainsi que des SÉISMES de VALKYRIES COLONISÉES et HOMICIDES D’AILLEURS s’exprimant dans un MANÈGE PUSILLANIME et IMPROVISÉ. »
Alors là franchement, un café qui évoque des séismes de valkyries je suis preneur !
Mon algorithme associe à un mot donné son équivalent poétique : c’est-à-dire le mot qui lui est le moins lié. Néanmoins, il ne permet a priori pas d’augmenter la poéticité du texte dans son ensemble. Les mots sont choisis indépendamment les uns des autres. C’est ainsi que, partant d’un BOUDIN aux POMMES nous pourrions arriver à un CANARD à l’ORANGE…
Il pourrait être intéressant de tester la robustesse de tout ça en utilisant d’autres dictionnaires. Des mots seraient ainsi ultra-poétiques s’ils sont poétiques au sens de plusieurs dictionnaires simultanément.
Enfin, il pourrait être amusant de calculer la poéticité en se basant sur des dictionnaires spécialisés tels que les dictionnaires de synonymes ou (mieux) les dictionnaires de rimes.
Méthode S + 7
Selon la définition donnée par l’Atlas de littérature potentielle de l’OuLiPo, la méthode S + 7 est une méthode de création de textes littéraires inventée par Jean Lescure consistant à remplacer dans un texte source chaque substantif par le septième substantif qui le suit dans un dictionnaire donné. Nous pouvons nous demander pourquoi avoir choisi cette valeur de 7 ? Pourquoi pas 2, 3 ou 121 ?
Il faut s’éloigner suffisamment loin du mot initial afin de perdre toute corrélation alphabétique éventuelle (AMOUR, AMOUREUX, AMOURACHER etc…) mais pas trop loin pour ne pas rendre l’exercice fastidieux.
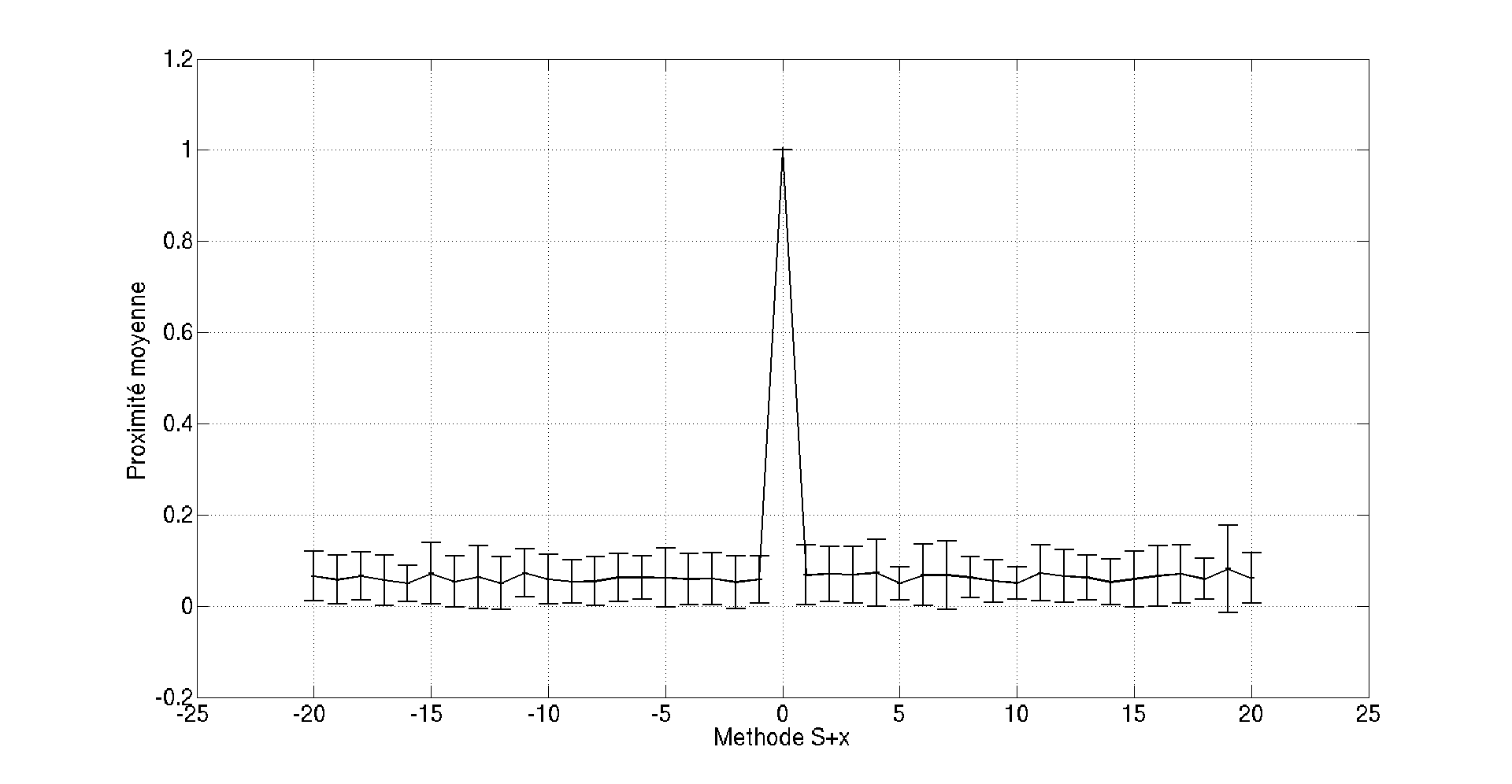
La figure ci-dessous montre la proximité moyenne de 30 mots donnés avec leur successeurs et prédécesseurs situés x places plus loin (x variant de -20 à 20). On voit que le choix de x n’a finalement que peu d’influence en moyenne… (bien que sur des cas particuliers, ce choix peut avoir son importance)
Savoir si un texte est poétique
« PRISONNIERS des GOUTTES d’EAU, nous ne sommes que des ANIMAUX PERPÉTUELS. Nous courons dans les VILLES sans BRUITS et les AFFICHES ENCHANTÉES ne nous touchent plus. À quoi bon ces grands ENTHOUSIASMES FRAGILES, ces SAUTS de JOIE DESSÉCHÉS ? Nous ne savons plus rien que les ASTRES MORTS ; nous regardons les VISAGES ; et nous soupirons de PLAISIR. » La Glace sans tain, Les champs magnétiques, d’André Breton et Philippe Soupault
« Les APPAREILS qui ont atteint la FIN de leur VIE UTILE ne doivent pas être consignés à la poubelle ! Des MATÉRIAUX utiles peuvent être récupérés des anciens appareils, par le recyclage. Pour assurer la SÉCURITÉ lors de l’ÉLIMINATION d’une VIEILLE MACHINE à LAVER, veuillez débrancher la PRISE de COURANT, couper le CÂBLE d’ALIMENTATION et le détruire avec la prise. Pour empêcher que les ENFANTS ne s’enferment dans la machine, cassez les CHARNIÈRES de la PORTE ou son DISPOSITIF de verrouillage. » Extrait du manuel d’utilisation de la machine à laver Candy Optima Wash System
Le premier texte est un extrait des Champs Magnétiques. Le second est un extrait d’un manuel de machine à laver. Arriverons-nous à dire que le premier appartient au domaine « poétique » alors que l’autre non ?
Les figures ci-dessous représentent les matrices de poéticité terme-à-terme des 18 premiers mots de chaque texte. Une couleur chaude (rouge) indique que les mots sont très proches, une couleur froide (bleu) indique que les mots sont distants. Du fait de la normalisation introduite tantôt, on observe que la diagonale est rouge : les mots entretiennent avec eux-même une proximité de 1. Ensuite, nous remarquons qu’il n’est pas évident de discerner parmi les deux images laquelle est la plus poétique (i.e. globalement la plus bleue). Pire, il semblerait même que le manuel de la machine à laver est légèrement plus poétique !
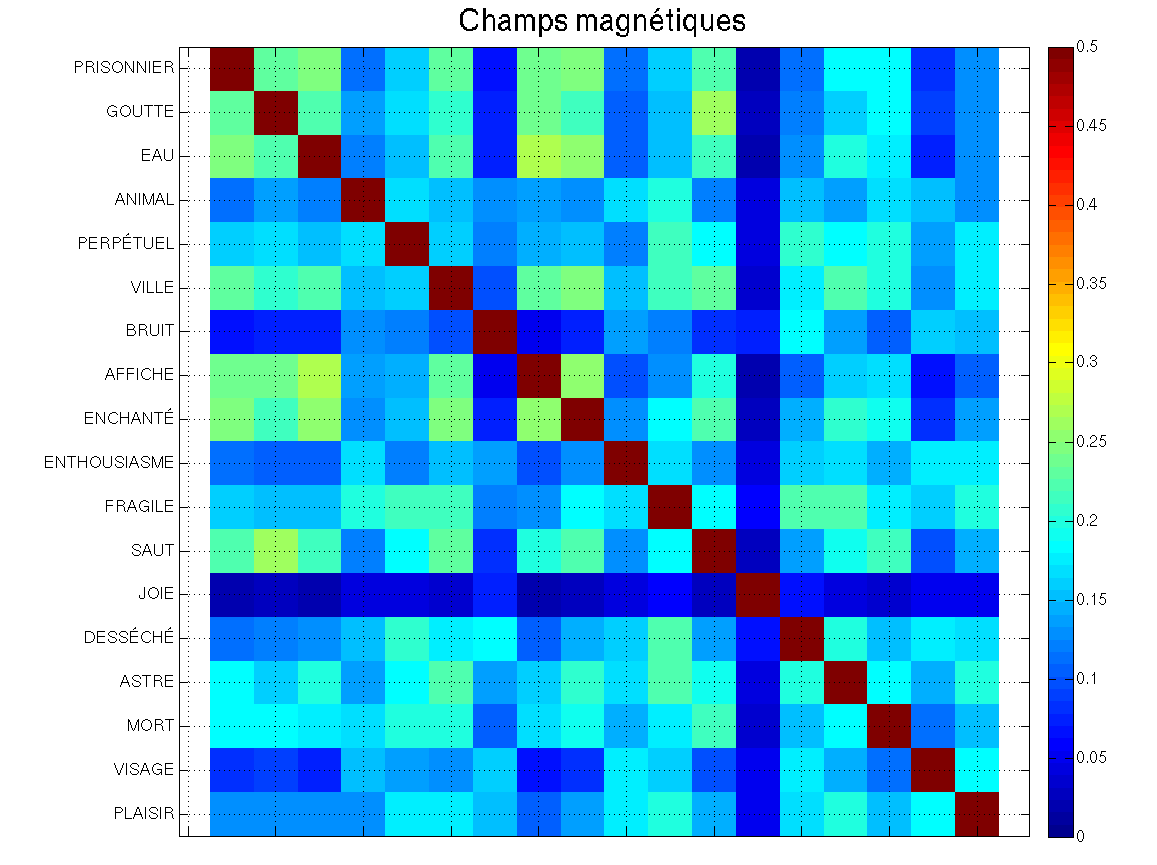
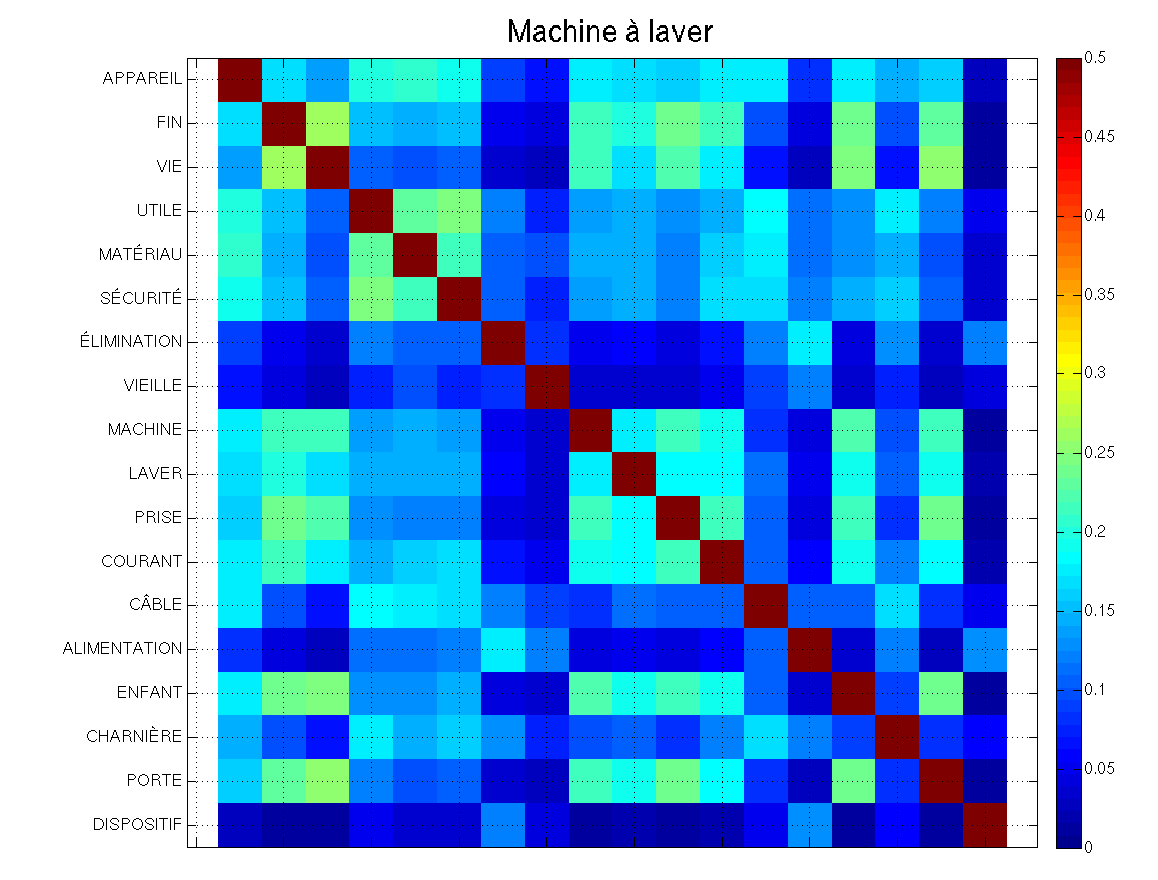
Qu’est-ce à dire ? Je vois trois explications possibles à ceci :
- ou bien la définition de notre estimateur de proximité n’est pas robuste,
- ou bien le Littré n’est pas assez détaillé pour épuiser toute la richesse informative de chaque mot : il y a des échos qui ne sont pas pris en compte,
- ou bien enfin, le Littré n’est pas purement informatif et contient une certaine part de poéticité (on l’a vu tantôt : CANARD et CURÉ sont liés).
Mais je pense que le gros point limitant est que le dictionnaire est trop petit : avec moins de 150 mots en moyenne pour définir chaque mot, il est difficile d’avoir une estimation fiable de la proximité : la majorité des mots n’ont rien à voir entre eux selon le Littré. Dès lors, s’il reste tout à fait possible de poétiser un texte comme nous l’avons fait tantôt, l’étude du Littré ne nous permet pas vraiment de comparer la poéticité de deux textes donnés car ils se trouveront généralement dans cette zone vague où les mots ne sont ni tout à fait proches, ni tout à fait étrangers : la grande majorité des textes aura ainsi peu ou prou la même poéticité.
Pour s’affranchir de cette limite, nous pourrions étudier les liens d’ordre plus élevé. Comparons les mots du dictionnaire à des personnes. Dans notre étude, nous avons établi que des mots étaient proches s’ils partageaient les mêmes définitions. On pourrait de la même façon dire que deux personnes sont proches si elles ont des enfants en commun (par exemple un homme et sa femme). Parallèlement deux mots étaient dualement proches s’ils étaient cités par les mêmes mots. Dans notre analogie, cela revient à dire que deux personnes sont proches si elles ont des parents communs (par exemple une soeur et son frère). Mais nous pourrions voir les liens plus lointains (grand-parents, oncles, cousins etc.). En pratique, il suffirait de refaire nos calculs en considérant les puissance n-ème de la matrice de liaison $M$ : $M^2$, $M^3$,… $M^n$.
Voici pour terminer, l’équivalent des figures précédentes pour « Un coup de dés jamais n’abolira le hasard » de Mallarmé.
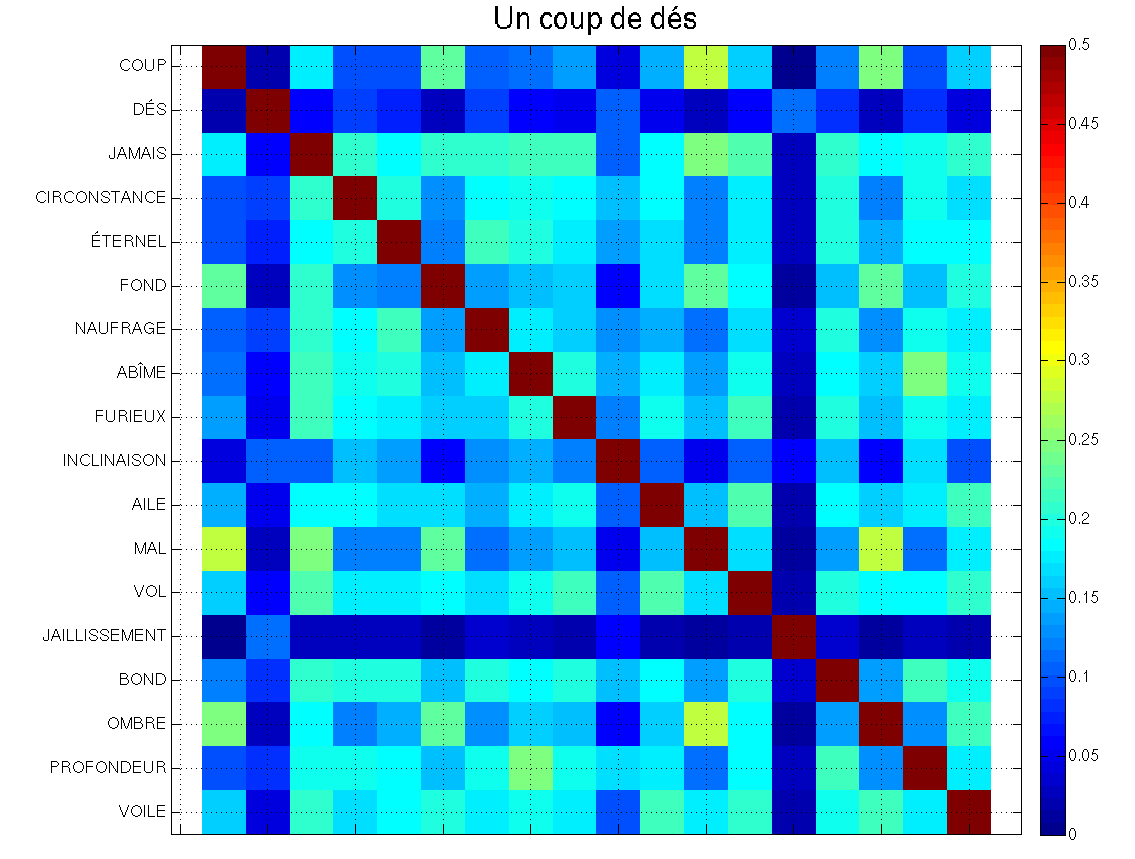
-
A noter toutefois qu’à l’heure actuelle, la dernière partie de cet article, qui concerne la poéticité des textes, n’a pas (encore) été modifiée. ↩