Résolution de l'oreille humaine
Cet article, très rapide, fait le point sur la résolution spectrale de l’oreille humaine.
Dans un précédent article, j’avais calculé le décalage théorique introduit par une corde en tension sur ses voisines lorsqu’on accorde une guitare. Cet effet était minuscule. Néanmoins on peut s’interroger sur la résolution spectrale de l’oreille humaine. C’est-à-dire quel est le plus petit décalage en fréquence qui puisse être perçu ? Est-ce le quart de ton ? Le huitième de ton ?
Protocole
J’ai développé un petit programme qui introduit des variations par rapport à un La de référence à $f_0 = 1760$ Hz. La variation est tantôt vers les aigus, tantôt vers les graves. On fait écouter les deux sons consécutivement pendant une seconde chacun et on demande au cobaye s’il a perçu une montée de fréquence ou une descente.
Cette expérience est reproduite $N=10$ fois sur un échantillons de $P=10$ variations différentes allant du demi-ton $k_0$ jusqu’à la 1024eme partie du ton (j’ignore comment on pourrait appeler cet écart…). On aura donc :
\[k_0 = 2^{1/12}\]Puis :
\[\begin{align} k_1 &= 2^{1/24}\\ k_2 &= 2^{1/48}\\ k_3 &= 2^{1/96}\\ \dots &\\ k_{9} &= 2^{1/6144} \end{align}\]Afin d’éviter les répétitions, le programme explore aléatoirement les $N\times{}P$ cas de test et choisit aléatoirement d’aller tantôt vers les aigus et tantôt vers les graves. On utilise ici une distribution uniforme avec une probabilité 1/2. On contraint également à ce que le ratio aigu/grave ne soit pas trop différent de 50/50.
Pour chaque valeur de variation (demi-ton, quart de ton etc.) on note le pourcentage de succès du cobaye. Ce sera simplement le nombre de bonnes réponses divisé par N, exprimé en pourcentage. On s’attend à de bonnes performances avec de grands écarts en fréquence et une baisse progressive à mesure que l’écart en fréquence diminue. Dès que l’écart franchit un certain seuil, on s’attend in fine à retrouver une distribution binomiale de paramètre 1/2 (un pile ou face). Avec $N$ assez grand, cela devrait se stabiliser autour de 50% de succès.
Les signaux générés sont de simples sinusoïdes pondérées par une fenêtre de Hanning $H$ :
\[s(t) = A \sin \left(2\pi f_0 k t \right)\times{}H(t)\]Résultats
Les résultats sont résumés dans la figure ci-dessous. Le taux de succès est tracé en fonction du ratio entre les notes allant du demi-ton (tout à gauche) jusqu’à la 1024eme partie du ton (tout à droite).
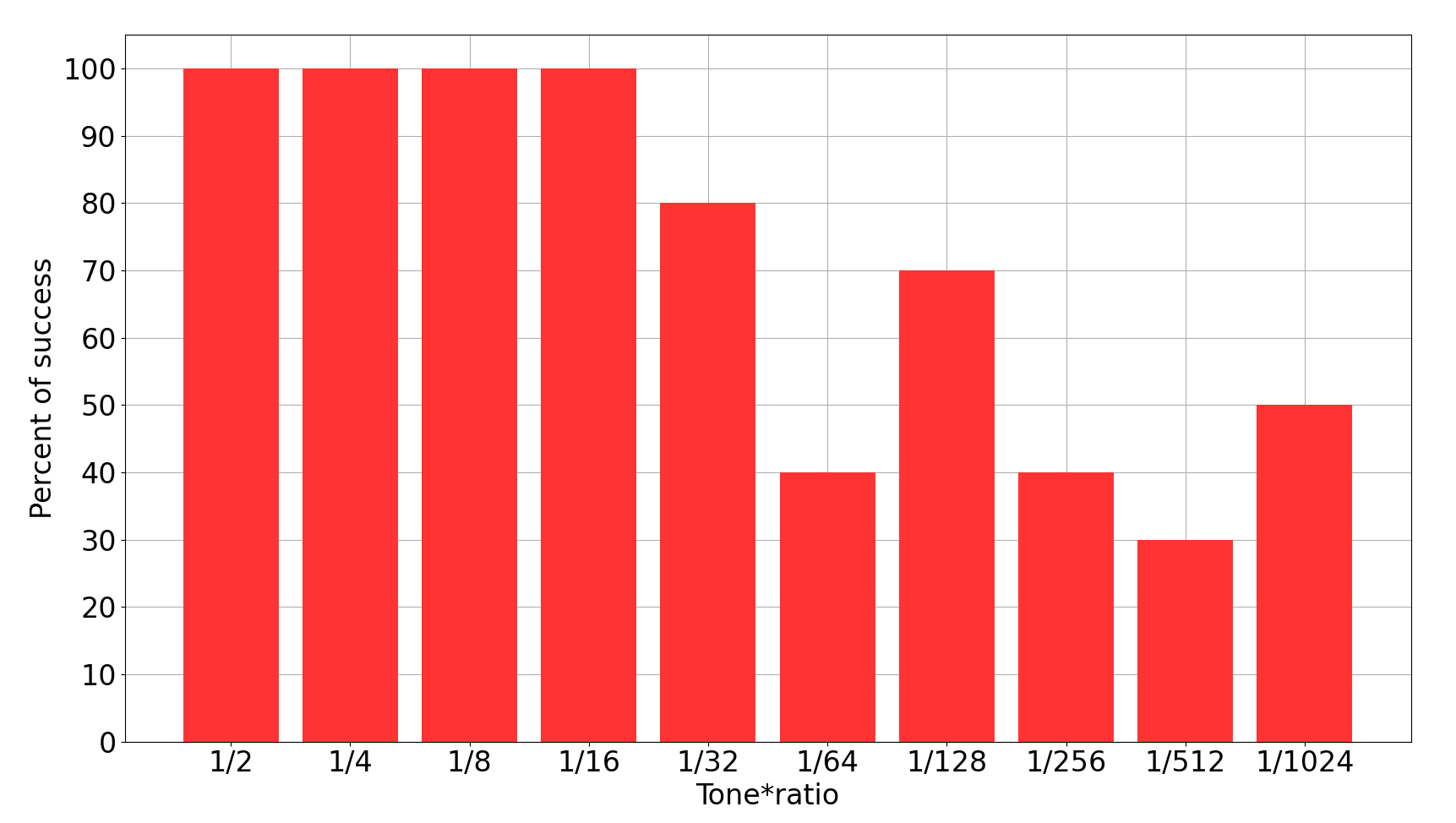
Les résultats sont excellents jusqu’au seizième de ton compris puis des erreurs surviennent. Il y avait clairement des cas où je ne percevais pas du tout la différence de hauteur et où je répondais un peu au hasard.
Un trente-deuxième de ton sur un La à 1760 Hz, cela représente un écart en fréquence de 6 Hz environ. Avec un soixante-quatrième de ton, on est à 3 Hz. Je n’ai pas trouvé de référence fiable sur le net (ça doit se trouver mais je ne veux pas passer trop de temps là-dessus). Néanmoins, il semble être établi que la résolution en fréquence de l’oreille humaine se situe aux alentours de 3 Hz ce qui est conforme avec ce que j’ai obtenu ici.
Discussion
Ce protocole fait l’hypothèse que la résolution spectrale est indépendante de la fréquence, ce qui est probablement faux. Mais enfin, cela permet d’avoir un premier ordre de grandeur. Et puis, juste avec 10 répétitions sur une plage de 10 variations, cela demande tout de même 100 points de mesure, ce qui est fastidieux.
On pourrait s’amuser à rajouter le calcul de la pvalue pour chaque pas de variation. Mais bon clairement avec uniquement $N=10$ répétitions, on a un échantillon trop faible pour en tirer quoi que ce soit de probant.
Enfin il pourrait être amusant de complexifier un peu le protocole en produisant une fondamentale et (par exemple) sa tierce légèrement altérée (soit vers les aigus soit vers les graves) et en demandant au cobaye d’estimer la justesse de la tierce. Cette fois-ci la justesse est évaluée par rapport à une note qui n’est pas jouée mais qui se déduit de la fondamentale : la tierce sonne-t-elle juste ou pas ?
Code en Python
Comme d’hab sous licence GPL.
Je pense que ce code peut être amélioré. En particulier :
- l’interface homme-machine est en ligne de commande sans traitement des exceptions (si on tape 2 au lieu de 0 ou 1, ça plante !)
- le jeu entre les indices pourrait être amélioré
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
Created on Mon May 24 18:02:51 2021
@author: donutman
@licence: GPL
"""
import numpy as np
from numpy import pi, sin, cos, sqrt
from scipy.special import erf as erf # might be used in the future for pvalue...
import simpleaudio as sa
from matplotlib import pyplot as plt, rc as rc
from time import sleep
# Parameters
fs = 44100 # 44100 samples per second
T = 1 # Note duration in seconds
N = 10 # Number of repetition
f0 = 2*2*440.0 # Initial frequency (La)
# half-tone, quarter-tone, eighth-tone etc.
ht = 2**(1/12) # Halt-tone multiplier, ie f' = ht*f and ht^12*f = 2f
kmult = np.arange(0,10) # half-tone, sqrt(halt-tone) = quarter-tone etc.
x = np.power(ht, 1/2**kmult)
Nht = len(x)
asking_tone = np.repeat(x, N)
# Some shuffle
ind = np.arange(Nht*N)
np.random.shuffle(ind)
asking_tone = asking_tone[ind]
# We want roughly 50% of each direction (higher or lower)
found=False
while (found==False):
freq_higher = np.random.rand(N*Nht)>0.5
found = (freq_higher.sum() > (N*Nht/2-5)) and (freq_higher.sum() < (N*Nht/2+5))
asking_tone = np.where(freq_higher==True, asking_tone, 1/asking_tone)
deltaf = asking_tone*f0 - f0
# y[k] = number of right answers for f = x[k]*f0
y = np.zeros(Nht)
# Time vector
t = np.linspace(0, T, T * fs, False)
# A quick function that plays 1s of a sine wave at f Hz
def play_sound(f):
s = sin(2*pi*f*t)*np.hanning(len(t))
s = (2**15-1)*s/s.max()
s = s.astype(np.int16)
play_obj = sa.play_buffer(s, num_channels=1, bytes_per_sample=2, sample_rate=fs)
play_obj.wait_done()
####### MAIN #####################################
# Here comes the main loop
for (k, kv) in enumerate(asking_tone):
print('- Asking %03d/%03d...' % (k+1, len(asking_tone)))
print(' - playing song one...')
play_sound(f0)
sleep(0.1)
print(' - playing song two...')
play_sound(f0*kv)
# p is the rank of the variation 0 <= p < Nht
p = int(ind[k]/N)
r = int(input(' - you heard an increase in the frequency ? (1 = yes, 0 = no) : '))
if (bool(r) == freq_higher[k]):
y[p] += 1
# Some plotting variables...
xl = np.arange(len(x))
xs = [('1/%d' % 2**(v+1)) for v in kmult]
rc('xtick', labelsize=24)
rc('ytick', labelsize=24)
# And here is the final bar plot !
plt.close('all')
plt.grid(zorder=0)
plt.bar(xl, y/N*100, zorder=3, color=(1, 0.2, 0.2))
plt.xticks(xl, xs)
plt.xlabel('Tone*ratio', fontsize=24)
plt.ylabel('Percent of success', fontsize=24)
plt.yticks(np.arange(0,110,10))