Tous les mots sont frères

Il y a quelques temps, nous nous étions amusés avec le Littré. J’aimerais aller un peu plus loin cette fois et creuser dans des directions tout juste ébauchées précédemment. En particulier, nous allons regarder les puissances itérées des matrices de liaison. Le lecteur peu familier avec les notations utilisées dans cet article est invité à se référer à l’article précédent.

Afin de varier un peu les plaisirs, je vais cette fois-ci me baser sur un dictionnaire des synonymes. Après quelques recherches, je me suis basé sur le dictionnaire de Frédéric Labbé, qui est diffusé sous license LGPL ¹. Bien qu’il soit précisé que des erreurs peuvent être présentes dans les entrées, nous réussissons à dégager certains résultats que nous présentons ici.

Note : les codes permettant la manipulation du dictionnaire de synonyme étaient initialement écrit en Matlab². Ils ont depuis été adaptés en Python et peuvent être librement récupérés à cette adresse. Les illustrations de cet article proviennent soit de la version Matlab soit de la version Python. Dans les deux cas, les codes se sont basés sur la même version du dictionnaire (2.3).

Plan de l’article

• Plan de l’article
• Introduction
• Degré polysémique et caractéristiques premières
• Mots riches, mots populaires
• Complétude et matrice de liaison
• Puissances itérées
  • Réflexion sur la complexité de la multiplication matricielle
  • Ensemble des synonymes d’ordre k
  • Algorithme de plus court chemin
    • Présentation de l’algorithme
    • Quelques réalisations du plus court chemin

Introduction

Une première observation importante est que pour la majorité des dictionnaires, l’entrée appartient généralement à la définition, autrement dit $\forall k\; m_k \in \sigma(m_k)$ presque partout. En effet, il est très possible que le mot “CHIEN” appartienne à la définition du mot “CHIEN”. Dans le cas d’un dictionnaire des synonymes c’est d’autant plus vrai : le mot “CHIEN” est nécessairement synonyme du mot “CHIEN”. Plus généralement un mot est toujours synonyme de lui-même de façon axiomatique.

Nous obtenons le même comportement avec un dictionnaire de rime : un mot rime toujours avec lui-même (et c’est même une rime riche je crois).

La seule exception que je trouve est le dictionnaire des antonymes : le mot “CHIEN” n’est pas antonyme de lui-même… J’ignore s’il existe des mots qui sont leur propre antonyme. Il faudrait peut être creuser du côté du méta-langage³.

Degré polysémique et caractéristiques premières

Notre dictionnaire des synonymes contient exactement 36 174 entrées.

La structure de ces entrées est légèrement plus complexe que celle du Littré précédemment étudié. Ici chaque entrée est définie non plus par un ensemble fini de mots (la définition) mais par un ensemble fini d’ensembles finis de mots (plusieurs définitions).

C’est obscur, j’en conviens… Regardons un exemple : quels sont les synonymes du mot “GUEULE” ?

gueule | 2

(Nom) | ouverture | bouche | mâchoires | crocs

(Nom) | visage (familier) | allure

Ici l’entrée “GUEULE” est définie par deux ensembles de mots, selon l’interprétation qu’on lui donne : parlons nous de la mâchoire d’un animal (ses crocs) ou bien du visage d’un homme (une belle gueule) ? Certains mots acceptent donc plusieurs définitions, on parle alors de polysémie. On appelle degré polysémique le nombre de définitions qu’un mot peut accepter.

L’essentiel des mots (99.91%) sont monosémiques, c’est-à-dire porteurs d’un seul sens.

• Seize mots sont polysémiques de degré 2, ce sont : Ave, bon, bougre, bravo, casse, César, chat, gueule, légalisation, maintenant, merdeux, mobile, peiner, quoi, rubis et tronche.
• Neuf mots sont polysémiques de degré 3 : fort, malade, merde, mode, modèle, nef, ours, père et terminal.
• Aucun mot n’est polysémique de degré 4.
• Deux mots sont polysémiques de degré 5 : folie et peine.
• Deux mots sont polysémiques de degré 6 : maître et mort.
• Un seul mot est polysémique de degré 7 : pratique.
• Un seul mot est polysémique de degré 8 : feu.
• Aucun mot ne possède un degré polysémique supérieur à 8.

Les 8 sens possibles que nous pourrions attribuer au mot “FEU” sont :

1. la lumière ou la lueur
2. la flamme c’est-à-dire la passion ou l’ardeur
3. l’âtre (au sens physique), c’est-à-dire la cheminée ou le brasier
4. la douleur ou la brûlure (pensons au feu du rasoir)
5. l’incendie (au sens de la destruction donc)
6. le signal (pensons aux phares ou aux sémaphores)
7. le combat, la fureur
8. enfin feu peut s’employer pour parler d’un défunt

Ainsi, bien que les liens de synonymies semblent le permettre, il pourrait être hasardeux de remplacer “je te déclare ma flamme” par “je te déclare la guerre”. A ce stade, je pense qu’il est commode de considérer les mots polysémiques comme autant de mots monosémiques qui auraient la particularité de partager la même orthographe⁴.

La distribution du nombre de sens est résumée dans la figure ci-dessous.

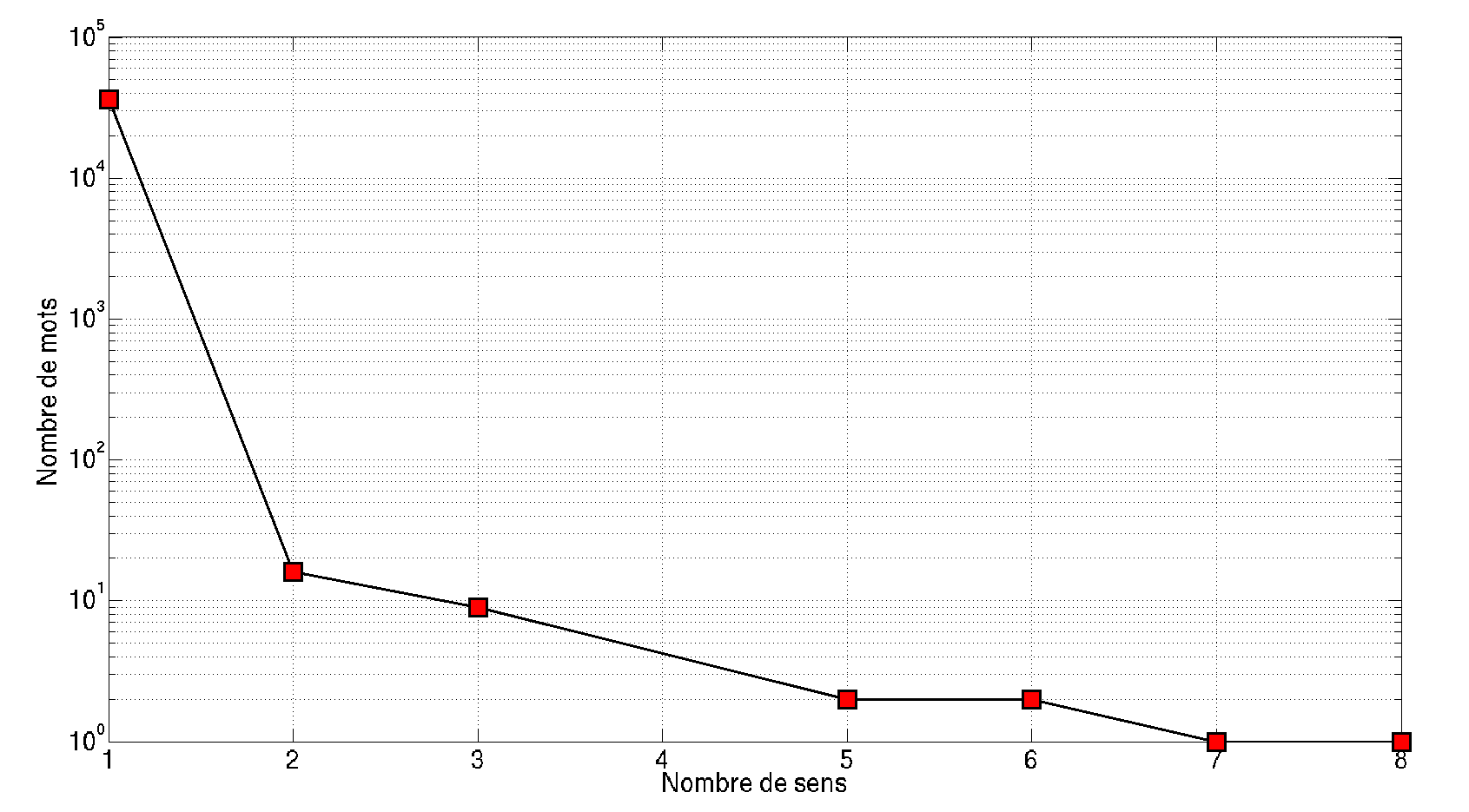
La particularité de la polysémie mise-à-part, le dictionnaire des synonymes est très similaire au Littré. Lorsqu’on regarde les synonymes sans tenir compte du degré polysémique (c’est-à-dire sans faire de distinguo entre les différents sens du mot), on parlera de méta-définition.

La figure ci-dessous représente la distribution de la longueur des méta-définitions. On remarque qu’en moyenne les mots sont définis en 11 synonymes (le Littré définissait de son côté les mots en 143 mots en moyenne). On peut saluer l’exemplaire concision du dictionnaire des synonymes. Par ailleurs, si certains mots n’admettent aucun synonyme, d’autres peuvent avoir jusqu’à 186 synonymes !

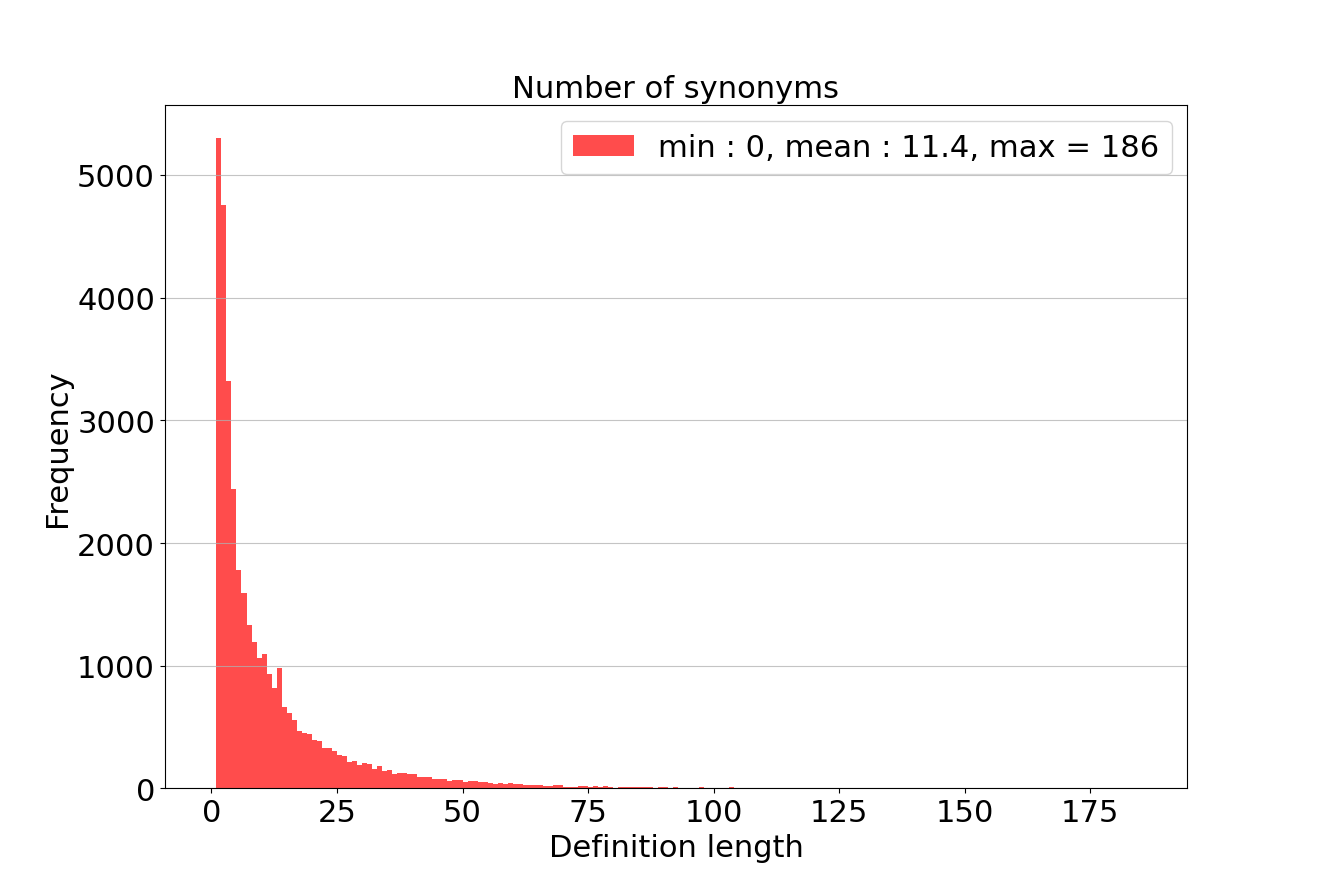
Mots riches, mots populaires

Les mots riches sont ceux qui admettent un maximum de synonymes. Dans notre cas d’étude, les 15 premiers mots riches sont les suivants :

Mots	Nombre de synonymes	Nombre de sens
trouble	186	1
délicat	184	1
fort	184	3
fin	176	1
vif	161	1
fixer	158	1
désagréable	152	1
abri	151	1
critique	150	1
grossier	146	1
ardeur	138	1
éclat	132	1
extraordinaire	129	1
accord	127	1
brillant	127	1

Nous voyons que le degré polysémique n’est pas vraiment corrélé à la richesse d’un mot. Dans les 15 premiers mots les plus riches, un seul mot (fort) n’est pas monosémique !

Réciproquement, un mot est d’autant plus populaire qu’il est fréquemment cité comme synonyme. Les 15 premiers mots les plus populaires sont ici :

Mots	Nombre de mots dont ils sont synonymes	Nombre de sens
trouble	186	1
fort	184	3
délicat	181	1
fin	175	1
vif	161	1
fixer	157	1
désagréable	152	1
abri	151	1
critique	147	1
grossier	146	1
dur	143	1
ardeur	138	1
éclat	131	1
extraordinaire	128	1
accord	127	1

Nous retrouvons à peu de chose près quasiment la même liste, nous y reviendrons dans la section suivante.

Complétude et matrice de liaison

Notre dictionnaire des synonymes est quasi-complet : presque tous les mots apparaissant dans les définitions sont également des entrées du dictionnaire. A minima, il faudrait enlever quelques mots mal orthographiés et supprimer quatre entrées⁵ pour que notre dictionnaire devienne complet. A partir de maintenant, nous supprimons ces entrées de notre liste et nous travaillons donc avec un dictionnaire rigoureusement complet (c’est crucial pour notre étude des puissances itérées). Dans le code Python, cette étape est effectuée par le script create_matrix.py.

Nous pouvons maintenant calculer la matrice de liaison⁶ de notre dictionnaire. Rappelons la définition de cette matrice $M_{i, j}$ :

\begin{array}{cccl} M(i,j) & = & 1 & si\; m_j \in \sigma(m_i) \ & & 0 & sinon \ \end{array}

$M_{i, j}$ vaut 1 si le mot $m_{j}$ apparaît dans une des définitions du mot $m_{i}$ et vaut 0 dans le cas contraire.

Si nous traçons l’allure de cette matrice, nous obtenons la figure suivante (le 1 est représenté par un pixel blanc et le 0 par un pixel noir).

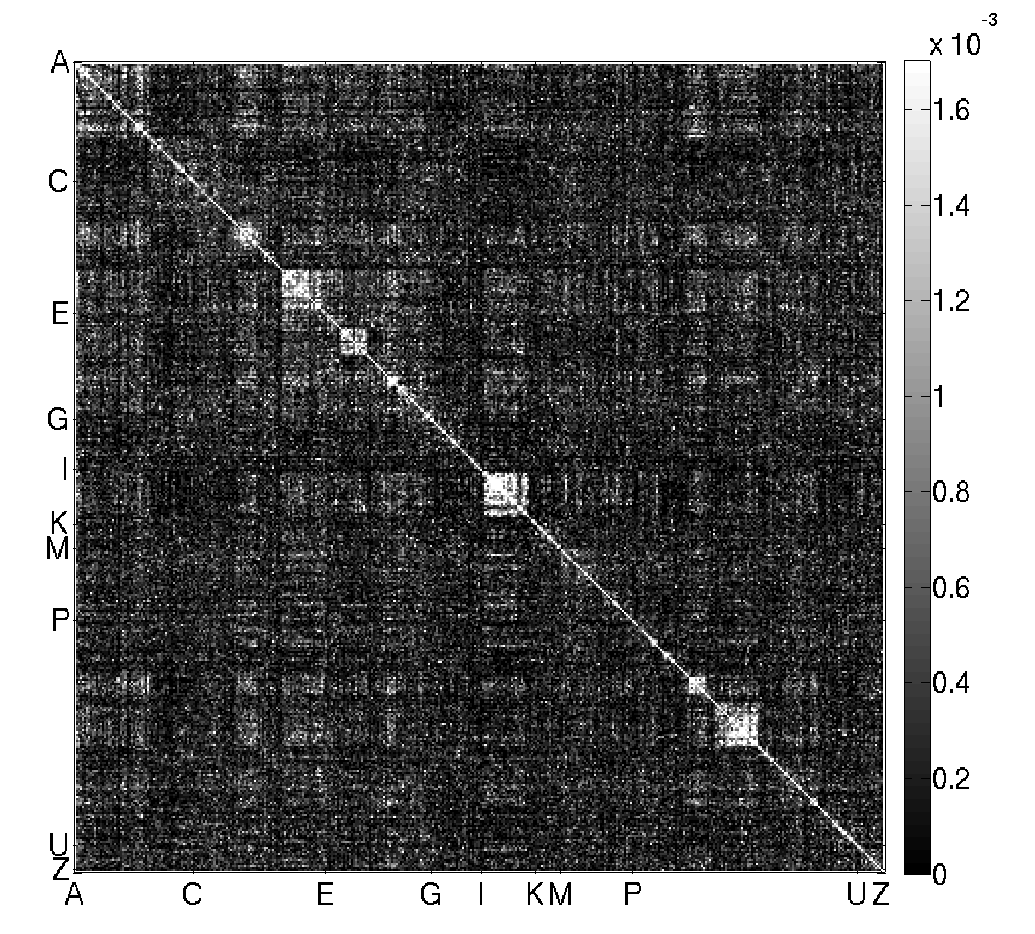
Nous observons tout d’abord, comme pour le Littré, la présence d’une belle diagonale blanche : les mots sont généralement synonymes d’eux même. Tout comme le Littré encore, la matrice est globalement sombre : la probabilité que deux mots choisis aléatoirement soient synonymes l’un de l’autre est très faible. Ceci est une conséquence directe du fait que le nombre de synonymes moyen d’un mot (11) est très inférieur au nombre de mots définis par le dictionnaire (36 174).

Par ailleurs, la matrice est très clairement diagonale : si $m_{i}$ apparaît dans les synonymes de $m_{j}$ alors $m_{j}$ apparaîtra vraisemblablement parmi les synonymes de $m_{i}$. C’est pour cette raison que les mots riches sont populaires, et réciproquement.

A la grande différence du Littré, les lignes verticales claires ont disparu : il n’y a plus de mots extrêmement populaires.

Enfin, nous voyons apparaître quelques carrés le long de la diagonale. Je ne sais pas bien à quoi ils correspondent, mais il s’agit probablement d’un artefact lié, d’une part à la structure des matrices aléatoires symétriques qui tendent à faire apparaître des motifs au voisinage de la diagonale et d’autre part au fait que certains mots synonymes ont la même racine (pensons à “jeu”, “jouet”, “joujou”)

Puissances itérées

Nous allons maintenant étudier les puissances itérées de la matrice M.

Autrement dit, on part d’un mot choisi au hasard et on regarde ses synonymes (première itération). Puis nous regardons les synonymes des synonymes (deuxième itération) et ainsi de suite jusqu’à ce que nous arrivions à un ensemble stable par M. Nous appelons ensemble des synonymes d’ordre k, l’ensemble de tous les synonymes rencontrés jusqu’à l’itération k incluse.

La question que nous nous posons alors est la suivante : jusqu’à quelle taille notre ensemble de synonymes va-t-il grandir ?

A priori, on pourrait naïvement penser que notre ensemble va rapidement converger vers un petit ensemble de mots plus ou moins liés à notre mot d’origine, mais entretenant tout de même avec lui une certaine proximité concevable.

Mais regardons cet exemple : léger → inconséquent → maladroit → gauche → lourd. Nous passons de léger à lourd uniquement par le jeu des relations de synonymie. Est-il possible que cet exemple puisse se généraliser et qu’on puisse relier deux mots quelconques par des liens de synonymies de longueur arbitraire ?

La polysémie des mots peut à ce propos faciliter cette dilution du sens. Dans notre algorithme de calcul Matlab lorsqu’un mot polysémique apparaît, nous retenons l’interprétation sémantique fournissant la plus grande proximité synonymique avec le mot d’origine. Partant de “briquet”, si nous tombons sur “feu” nous choisirons le feu en tant que flamme et non pas en tant qu’ardeur. Précisons ici que nous ne savons absolument pas ce que “briquet”, “feu” ou “ardeur” signifient : toute l’information est contenue exclusivement dans la matrice M et dans le découpage de la méta-définition en N sous-ensembles. Comme indiqué en introduction, nous considérons donc que les différentes significations du mot “feu” sont d’autant de mots distincts qui partagent la caractéristique curieuse de s’écrire de la même façon. Notre algorithme en Python ne contient pas encore cette subtilité.

Avant d’aller plus loin, il faut néanmoins disgresser rapidement sur les limitations des moyens de calcul dont nous disposons. On verra que ceci nous conduira à deux approches complémentaires pour étudier nos puissances itérées.

Réflexion sur la complexité de la multiplication matricielle

Selon les algorithmes et les matrices considérés, la complexité de la multiplication matricielle $c$ varie entre $\mathcal{O}(n^2)$ (qui est un minorant strict) et $\mathcal{O}(n^3)$. Dans le cas de notre dictionnaire de synonyme où, rappelons-le, $n$ est de l’ordre de $3\cdot{}10^5$, cela représente entre $10^{10}$ et $10^{16}$ opérations ce qui est prohibitif même en considérant des matrices de booléens.

Néanmoins, la matrice que nous considérons est certes de grande dimension, mais la plupart de ses coefficients sont nuls (rappelons-nous que chaque mots est définis en moyenne par 11 autres mots). Nous pouvons tirer parti de cette caractéristique pour améliorer grandement le temps de calcul. Notre matrice d’adjacence sera ainsi représentée par une matrice creuse. Sous Matlab, cela revient à utiliser la fonction sparse; sous Python il s’agira des fonctions coo_matrix(), csr_matrix() ou csc_matrix() du module scipy.sparse.

La performance de la multiplication matricielle de matrices creuses est très fortement impacté par le nombre de valeurs non nulles de la matrice. Les calculs seront ainsi très rapides lorsque la matrice est très creuse et les performances se dégraderont lorsque la matrice se remplit. Il se peut même qu’au-delà d’un certain seuil de remplissage, les performances soient moindres que dans le cas du calcul naïf.

Ceci est illustré dans la figure ci-dessous où nous avons considéré des matrices aléatoires à coefficients entiers de taille $1000\times{}1000$. Le temps de calcul est représenté en fonction du taux de remplissage des valeurs non-nulles dans le cas des matrices creuses (courbe rouge) et dense (courbe bleue). Si le calcul classique est relativement indépendant du taux de remplissage, on voit très clairement que le calcul via les matrices creuses est fortement impacté : au-delà de 80% de remplissage, les performances sont pires que dans le cas du calcul classique. La gigue qu’on observe provient du fait qu’on considère des matrices aléatoires et que nous n’avons réalisé qu’un seul tirage à chaque étape.

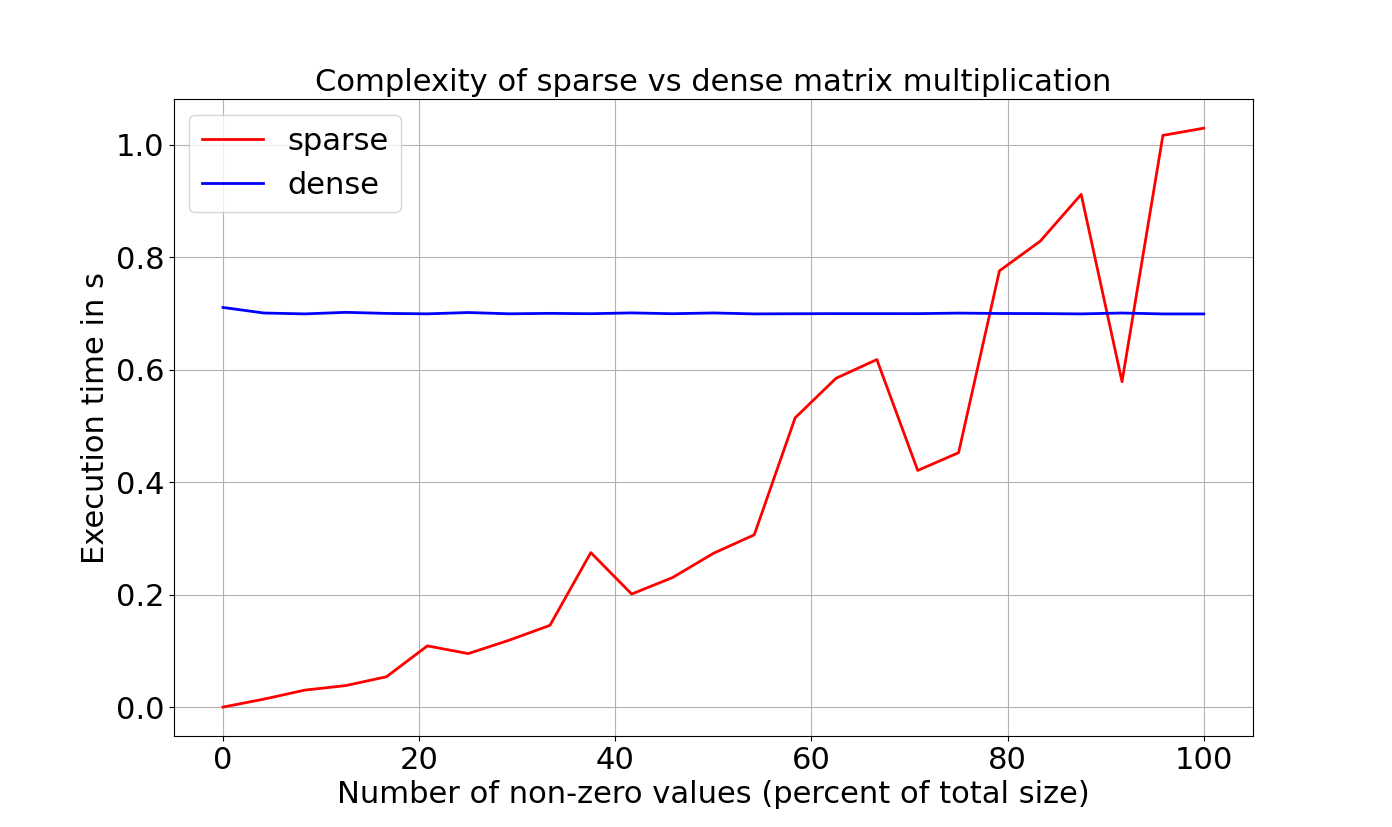
Dans le cas d’une matrice aléatoire de booléens de dimension $36000\times{}36000$ (plus proche de notre cas pratique), on voit clairement ci-dessous que le temps de calcul de l’élévation au carré dépend drastiquement du taux de remplissage.

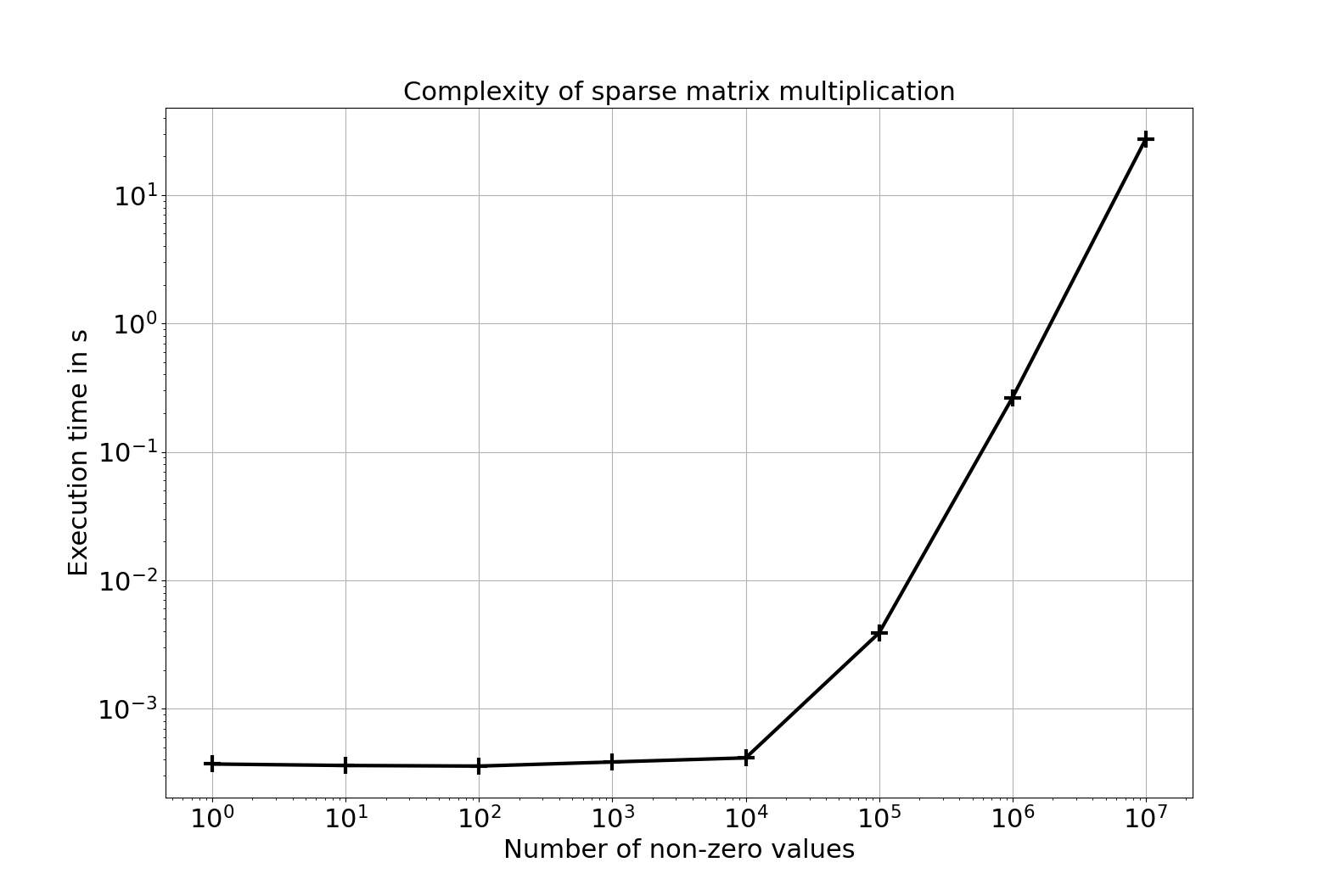
Notre matrice initiale est remplie environ à $0.07$%, sa première itération l’est à $2$% (donc on a tout de même multiplié par 30 le nombre de valeurs non-nulles). Très vite, il devient impossible de calculer les puissances suivantes.

On pourrait éventuellement diminuer le coup du calcul en ne gardant à chaque itération que les classes d’équivalences des ensembles de synonymes pour éviter de recalculer plusieurs fois la même chose. On pourrait également tirer parti de la symétrie de la matrice M pour accélérer les calculs. Ce sont des pistes à creuser.

Mais dans l’immédiat, nous avons opté pour deux approches complémentaires :

1. Plutôt que de construire les dictionnaires itérés de tous les mots, on décide de ne partir que d’un seul mot et de regarder croître son ensemble des synonymes : c’est l’ensemble des synonymes d’ordre k dont nous parlions plus haut. Ceci nous permettra d’étudier certaines trajectoires et de dégager des comportements communs (mais sans avoir la garantie que l’ensemble des mots suit cette tendance).

2. Partant de deux mots donnés, nous cherchons à construire un chemin via notre matrice d’adjacence.

Ensemble des synonymes d’ordre k

Sous python, il faut appeler la fonction compute_syno_set(graph, word) qui renverra un tuple contenant la liste des tailles des ensembles de synonymes à chaque itération (jusqu’à stabiliser l’itération au sens de taille d’ensemble ou bien lorsqu’on dépasse un nombre d’itération maximum, par défaut fixé à 20).

def compute_syno_set(graph, word, itermax=20):
    if (not word in names):
        print('Error : %s does not belong to the dictionary' % word)
        return
    
    M = graph.todense()
    
    ind = table[word]
    syno_set = set([ind])
    size_set = 1
    iteration = 1
    
    size_set_vect = [size_set]
    iteration_vect = [iteration]
    
    same_size = False
    
    while (same_size==False) and (iteration < itermax):
        print('Iteration %d...' % iteration)
        # We construct the set
        for k in syno_set:
            line = np.array(M[k][:]).flatten()
            new_syno = np.where(line==True)[0]
            syno_set = syno_set.union(set(new_syno))
        
        if len(syno_set) == size_set:
            same_size = True
        
        size_set = len(syno_set)
        
        size_set_vect.append(size_set)
        iteration += 1
        
         
    iteration_vect = range(0, iteration)
        
    return (iteration_vect, size_set_vect)

Nous regardons dix mots choisis aléatoirement : active, dune, esquille, grive, hors champ, imperméabilité, insurmontable, tâches, tram et vermiculaire.

Pour chacun de ces mots, la taille de l’ensemble des synonymes d’ordre k a été tracée en fonction de k.

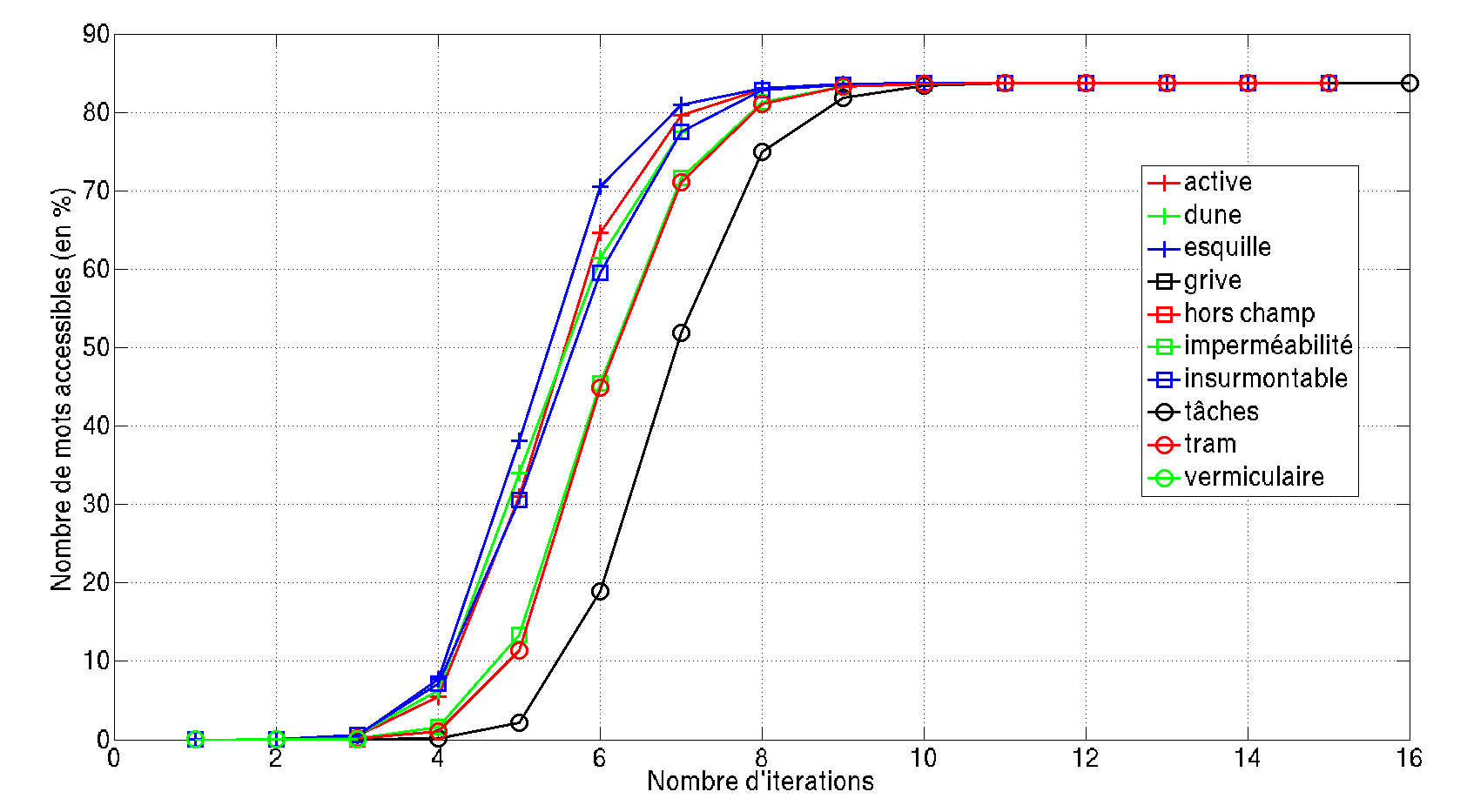
Tous ces mots convergent assez rapidement (environ 10 itérations) vers un ensemble stable par l’opération de synonymie. Par ailleurs, ils ont tous grandi très rapidement et semblent saturer vers la même limite : plus de 80% de l’ensemble des entrées du dictionnaire ! J’émets l’hypothèse qu’il s’agit du même ensemble.

On pourrait continuer l’exploration plus avant et définir des classes d’ordre k des mots : deux mots appartiennent à la même classe synonymique d’ordre k si et seulement si ils peuvent être reliés par au plus k itérations successives de la matrice de liaison.

Néanmoins l’inconvénient de cette approche est qu’on ignore complétement le contenu de nos ensembles successifs. Est-il pertinent qu’un ensemble de synonyme contienne 80% de l’ensemble des mots ? C’est ce que nous allons voir à la section suivante.

Je tiens toutefois à remarquer que ce résultat peut être contaminé par plusieurs effets :

1. nous avons expliqué comment nous avons tenté de limiter la contamination des mots polysémiques. Néanmoins, il est facilement entendable qu’un erreur de sens à une étape de l’itération peut faire grimper artificiellement la taille de notre ensemble de synonymes. Ceci étant dit, il n’existe finalement que très peu de mots polysémiques, leur impact est peut être négligeable. Une solution simple pour résoudre ce problème pourrait être de simplement supprimer du dictionnaire tout mot polysémique et de vérifier si cela impacte nos résultats.
2. ce dictionnaire de synonyme n’est pas parfait et, sans parler d’erreurs manifestes qui peuvent être présentes, on peut s’interroger sur la pertinence de certains synonymes. Par exemple “poisson” admet comme synonyme “marée”.
3. Nous avons considéré les synonymes comme tous équivalents. Or, comme discuté sur le forum de Grammalecte, il y a des nuances entre eux : on pourra parler d’hypernonyme (“céréale” pour “blé”), d’hyponymes (“froment” pour “blé”) voire de synsets (dont la définition, je pense, rejoint un peu celle de polysémie que nous employons). Prendre en compte ces nuances peut avoir un impact sur nos résultats.

Quoiqu’il en soit, afin de vérifier plus en détail les relations entre les mots, nous avons adapté un algorithme de plus court chemin et les résultats sont surprenant. C’est l’enjeu de la section suivante.

Algorithme de plus court chemin

Présentation de l’algorithme

Il existe plusieurs algorithmes de plus court chemin, basé sur la structure de notre graphe. Dans notre cas, le graphe de liaison des synonymes est :

1. fini : en ce sens que les mots existent en nombre fini
2. orienté : en ce sens que si $m_i$ est synonyme de $m_j$, cela n’implique pas nécessairement que $m_j$ soit synonyme de $m_i$
3. non pondéré : tous les chemins ont le même poids⁷

Un exemple de tel graphe est donné ci-dessous. Vous remarquerez que les chemins sont 1/ orientés et 2/ possèdent la même pondération.

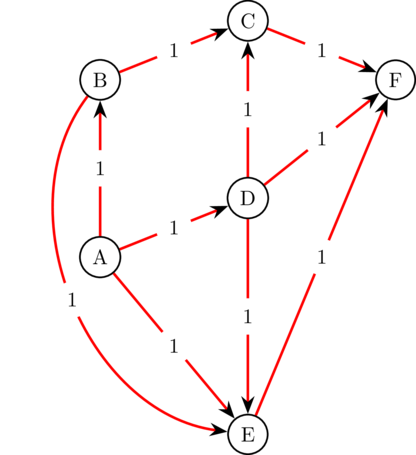
L’algorithme le plus répandu pour résoudre ce type de minimisation est l’algorithme de Dijkstra, qui date de 1959.

La fonction dijkstra(graph, nodes, node_start, node_end) du fichier simple_dijkstra.py en donne une implémentation fonctionnelle. On pourrait se baser sur cette version de l’algorithme pour étudier nos synonymes mais le module scipy.sparse en fournit une version optimisée pour les matrices creuses et tirant parti des tas de Fibonacci. Son prototype est le suivant :

sparse.csgraph.dijkstra(graph, directed=True, return_predecessors=True,
                            indices=[ind1], limit=limit,
                            unweighted=True, min_only=False)

Quelques réalisations du plus court chemin

La fonction sparse.csgraph.dijkstra() a été encapsulée dans la fonction shortest_path(word1, word2)

J’ai pu trouver de très jolis chemins reliant des mots en apparence très éloignés. Comment, par le biais de synonymes successifs, transformer un “minable” en “héros” ? Une “princesse” en “grenouille” ? Comment passer d’une “tarte” à un “chien”; d’une “mosquée” à une “usine”; d’un “salon” à un “lac” ou d’un “roi” à un “oiseau” ? L’exercice ne me paraît pas simple du tout.

Voici par exemple le chemin reliant “poisson” à “chat” : poisson -> marée -> flot -> vague -> inhabité -> fauve -> félin -> chat. On se rend compte qu’on s’éloigne de plus en plus de la thématique du poisson (l’eau, la mer) pour se rapprocher de celle du chat (le fauve, le sauvage, le lointain). Dans ce pont qui se dresse, la clef de voûte est le mot “vague” qui fait la transition et relie ces deux thématiques. Il y a donc une ambiguïté dans le mot “vague”, ambiguïté grâce à laquelle on peut passer d’un poisson à un chat. On soulignera de nouveau que certains synonymes sont moins heureux que d’autres (la “marée” synonyme de “poisson”).

Voici d’autres réalisations (les mots que j’estime ambigus apparaissent en gras) :

• marionnette → mannequin → reproduction → postérité → enfant
• table → inventaire → sommaire → brut → fauve → félin → chat
• tarte → chou → mignon → délicat → susceptible → hargneux → chien
• minable → commun → éprouvé → brave → héros
• roi → autocrate → chef → coq → oiseau
• musique → enregistrement → bande → attache → anneau → tire-fond → boulon
• éléphant → mammouth → géant → espace → multitude → assemblée → bouquet → fagot → ligot → allumette
• salon → chambre → assemblée → afflux → eau → lac
• mosquée → temple → église → groupe → atelier → usine
• princesse → altesse → excellence → élévation → bosse → roussette → grenouille
• poisson → marée → flot → vague → inhabité → fauve → félin → chat
• clou → aiguille → cariatide → idole → dieu
• clé → crochet → agrafe → bijou → boule → pomme

La conclusion immédiate qui semble se dégager de tout cela est que, contrairement à ce qu’on affirmait au début de l’article, l’essentiel des mots monosémiques sont porteurs d’une ambiguité intrinséque et pourraient ainsi être considéré comme polysémiques. Parle-t-on de la reproduction en tant qu’objet manufacturé (les marionnettes sont toutes des reproductions) ou en tant que processus biologique qui créé des enfants ?

Cette ambiguïté ne semble pas être le fait seul de notre dictionnaire des synonymes puisqu’on la retrouve également dans d’autres dictionnaires comme par exemple celui du Centre national de ressources textuelles et lexicales (CNRTL). Vous observez que dans la liste des synonymes de “sommaire”, “résumé” et “rudimentaire” apparaissent au même niveau alors qu’ils ne sont pas porteurs du même sens.

L’étape d’après pourrait être de tracer pour chaque mot-noeud du chemin la distance qui le sépare du mot initial (d’une part) et la distance qui le sépare du mot final (d’autre part). Le mot ambigu pourrait être alors facilement repéré : c’est le croisement entre les deux courbes. Il nous faudrait toutefois un estimateur fiable de la distance sémantique entre les mots. Il faudra également envisager le cas des chemins présentant plusieurs mots ambigus, comme dans le chemin ci-dessus qui nous fait passer d’une “tarte” à un “chien” en passant par “chou” et “délicat”.

1. à ma connaissance, c’est le seul dictionnaire de synonyme français libre, voir par exemple cette discussion sur linuxfr.org ↩

2. première version du site sous Spip, article intialement écrit le 30/03/2016 ↩

3. on peut ici penser au paradoxe hétérologique de Grelling-Nelson. Considérons un nouvel adjectif que nous appelons “hétérologique”. Un mot est hétérologique s’il ne s’applique pas à lui même. Ainsi “long” est hétérologique car le mot “long” n’est pas long. De même, “illisible” est également hétérologique puisque parfaitement lisible. ↩

4. on parle alors d’homographie. Impossible à ce stade de ne pas mentionner les rimes riches d’Alphonse Allais et cette histoire, que je ne retrouve plus, où il donne conseil à un poète étranger. C’était une géniale généralisation autour de phrases telles que “les poules couvent au couvent”. ↩

5. les mots à supprimer sont : acétimètre, cornemuseux, emmerdes et firmware. ↩

6. en employant le vocabulaire de la théorie des graphes, on pourrait aussi parler de matrice d’adjacence ↩

7. ce n’est pas le cas de tous les dictionnaires, regardez le dictionnaire du CNRTL ↩